
* The notion that matter might be divisible into fundamental "atoms" goes back to antiquity, but it wasn't until the 19th century that the notion of atoms, and their classification, became an accepted reality. In the early 20th century, physicists began to probe the atom more deeply, to find that it had constituent particles itself -- and to then characterize exactly why atoms had the properties they did.
* We have already seen the solution to the Schroedinger equation for the infinite square well. The solution to the equation for even the simplest atom, the hydrogen atom, consisting of a single electron orbiting around a nucleus with a single positive charge, is much more complicated. Although the infinite square well could be bent around into a ring, plugging in the simple substitution:
L = 2 * PI * radius
-- to give exactly the same result in terms of the radius of the ring instead of the length L, this doesn't really model the orbit of an electron around an atomic nucleus, where an electron can move in three dimensions.
Deriving a solution of the Schroedinger equation for the hydrogen atom is far beyond the scope of an elementary document, but the solution itself can be explained. In the case of the infinite square well, the electron is constrained to have energies of specific levels; in the case of an atom, it is constrained into sets of "atomic orbitals" with a three-dimensional configuration.
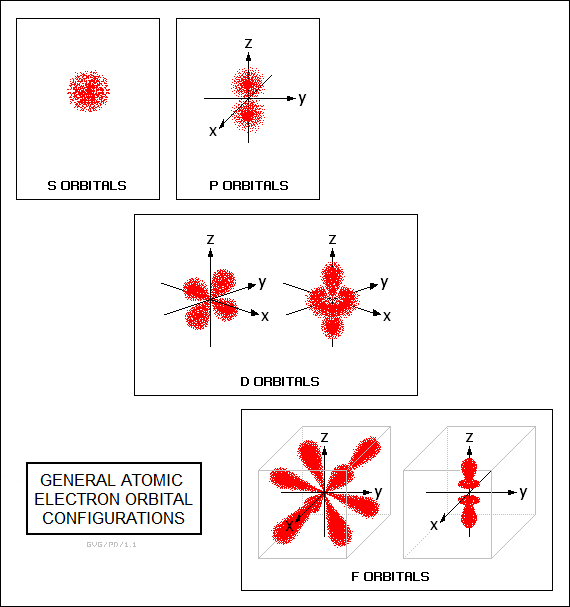
The orbitals are generally drawn as three-dimensional graphs of spheres; or two ellipsoids in a dumbbell configuration, or four ellipsoids in a four-leaf clover configuration; and so on, with the more complicated orbitals looking something like the sort of thing a clown might create by twisting balloons and tying them together. Given the probabilistic nature of quantum mechanics, these graphs are really probability distributions, defining the regions of space where an electron is likely to be observed and with no actual sharp boundary. A "boundary surface" usually defines a 99% probability.
In the case of the infinite square well, the energy states of the system are defined by a single quantum number n, with integer values from 1 to infinity. As discussed briefly earlier with regards to the development of the Bohr atomic model, the states of the electron in the hydrogen atom are also defined by the quantum number n in this case, as well as three other quantum numbers:
Each orbital of the hydrogen atom is defined by these four quantum numbers. The n quantum number is called the "principal quantum number". It gives the average size of the orbitals. By convention, the values of the principal quantum number are assigned letter designations as follows, though this scheme is no longer in popular use:
1: K 2: L 3: M 4: N 5: O
The "l" quantum number is called the "subsidiary" or "azimuthal" quantum number, and its values are also assigned letter designations as follows, with these designations still in common use:
0: s 1: p 2: d 3: f 4: g
The "ml" quantum number is called the "magnetic" quantum number, since the orientation of the orbital makes a difference in electron energy if the hydrogen atom is in a magnetic field. Finally, the "ms" quantum number is called simply the "spin" quantum number.
Electron orbitals are organized into "shells" by the primary quantum number, with each shell organized into "subshells" by the secondary quantum number. The following table shows the organization of the shells and subshells, along with the number of orbitals. The spin quantum number is not listed, since it always has values of U and D for each orbital, doubling the number of orbitals:
subshell shell
n l ml orbitals orbitals
________________________________________________________
1:K 0:s 0 2 2
2:L 0:s 0 2
1:p -1 0 +1 6 8
3:M 0:s 0
1:p -1 0 +1 6
2:d -2 -1 0 +1 +2 10 18
4:N 0:s 0 2
1:p -1 0 +1 6
2:d -2 -1 0 +1 +2 10
3:f -3 -2 -1 0 +1 +2 +3 14 32
5:O 0:s 0 2
1:p -1 0 +1 6
2:d -2 -1 0 +1 +2 10
3:f -3 -2 -1 0 +1 +2 +3 14
4:g -4 -3 -2 -1 0 +1 +2 +3 +4 18 50
________________________________________________________
The electron in the hydrogen atom can occupy any of these or higher orbitals; in its lowest energy or "ground" state, it occupies the orbital with n = 1 and l = 0. If the electron is hit by a photon or otherwise energized, it jumps to one of the higher "excited" orbitals. If the energy is great enough, the electron is knocked from of the atom completely. The amount of energy required to kick the electron out of the atom is known as the "ionization energy".
BACK_TO_TOP* The Schroedinger equation can only be solved exactly for single-electron atoms -- that is hydrogen, or more complicated atoms that have been ionized and lost all of their electrons but one. In such a case, the single electron is orbiting around the positively-charged nucleus under the influence of attractive electric force. Adding other electrons to an atom sets up repulsive forces between the electrons, which greatly complicates the scenario. However, approximate and numerical methods can be used to give as precise a solution as is required, and in any case, the general arrangement of the orbitals as described for the hydrogen atom -- with the quantum numbers n, l, ml, and ms -- remains true for more complicated atoms.
According to the Pauli exclusion principle, no two electrons can occupy the same energy state, so in the ground state of such atoms the electrons will occupy separate orbitals. One of the interesting features of this scheme is that atoms are inclined, from an energetic point of view, to fill up their outer shell:
The electrons in the outermost shell of an atom are referred to as "valence" electrons. It is this shell-filling behavior, established by the Schroedinger wave equation and the Pauli exclusion principle, that results in the periodic table of the elements. The periodic table is organized as follows, with the elements given by their abbreviations and accompanied by their "atomic number (Z)", which is the number of protons in the nucleus of the atom:
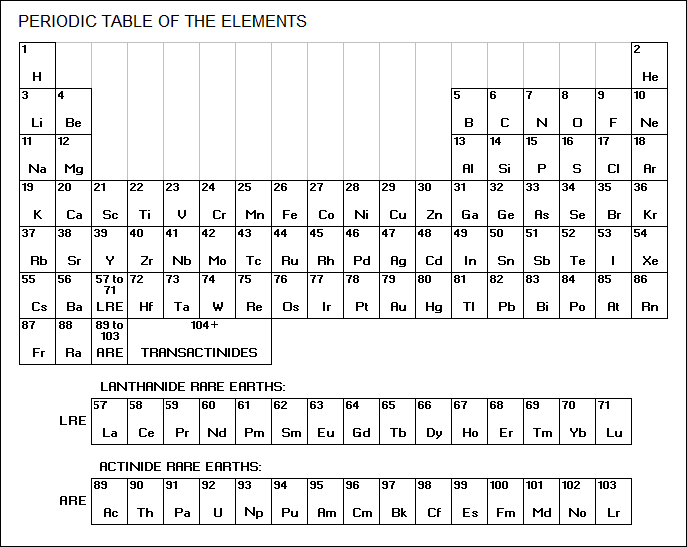
For example, in its ground state the hydrogen (H) atom has a single electron in its n = 1, l = 0 / s, orbital. This can be conveniently represented in a shorthand as follows:
1s1
-- where the trailing "1" gives the number of electrons in the shell. When n = 1, there's only one l = 0 / s orbital in the shell, which can accommodate up to two electrons -- one with spin U, one with spin D. Since the outer shell of hydrogen is half-full, it tends to lose or acquire an electron about as easily, and is reactive.
The helium (He) atom has two electrons, and so its ground-state configuration can be represented as:
1s2
This gives helium a full outer shell, and so it's inert. It is one of the "noble gases", which all are inert, and occupy the rightmost column of the periodic table. Incidentally, the "1s" orbital is spherical.
* With n = 1, only two electrons can be accommodated, so the ground state of the next element, lithium (Li, with Z = 3), includes a second shell, with n = 2. Its ground-state configuration is given as:
1s2:2s1
-- or, since the 1s2 configuration is that of helium, as:
[He] 2s1
As shown earlier, the shell defined by n = 2 can accommodate eight electrons, so the ground-state electron configurations of this next row of the periodic table are built up as follows:
Z element symbol configuration
______________________________________________
3 lithium Li [He] 2s1
4 beryllium Be [He] 2s2
5 boron B [He] 2s2:2p1
6 carbon C [He] 2s2:2p2
7 nitrogen N [He] 2s2:2p3
8 oxygen O [He] 2s2:2p4
9 fluorine F [He] 2s2:2p5
10 neon Ne [He] 2s2:2p6
______________________________________________
As this table suggests, lithium easily loses an electron and fluorine easily accepts one, so both are reactive, while carbon has an intermediate reactivity. Of course neon, with a full shell, is inert -- a noble gas. The 2s orbital is, like the 1s orbital, spherical.
There are three 2p orbitals. All have two lobes, like two raindrops stuck together at their pointy ends, and are oriented along the X, Y, and Z axes, being designated "Px", "Py", and "Pz" accordingly. Incidentally, since electrons have the same charge and repel each other, two electrons with opposed spins will not share the same orbital if there is an empty orbital in the same subshell: nitrogen has one electron in each of its three 2p orbitals. This is known as "Hund's Rule", after the German physicist Friedrich Hund (1896:1997).
* The third row of the table of course involves filling up the shell for n = 3 and begins with sodium (Na, Z = 11), which has the ground-state electron configuration of:
[He] 2s1:2p6:3s1
-- or, simplifying:
[Ne] 3s1
The electron configurations of this row are built up as follows:
Z element symbol configuration
______________________________________________
11 sodium Na [Ne] 3s1
12 magnesium Mg [Ne] 3s2
13 aluminum Al [Ne] 3s1:3p1
14 silicon Si [Ne] 3s1:3p2
15 phosphorus P [Ne] 3s1:3p3
16 sulfur S [Ne] 3s1:3p4
17 chlorine Cl [Ne] 3s1:3p5
18 argon Ar [Ne] 3s1:3p6
______________________________________________
This parallels essentially the same pattern of reactivities as the second row: sodium and chlorine are highly reactive, silicon has an intermediate reactivity, and argon is an inert noble gas. However, an astute reader will get suspicious on reading this, since for n = 3 there should a set of "d" orbitals as well, with a capacity of 10 electrons, giving the shell a total capacity of 18 electrons. Why, then, are there only eight elements in the third row?
The reason is that in the ground state of the atom, electrons unsurprisingly fill the orbitals with the lowest energy, and the energy levels of the orbitals don't track the primary quantum number n in a nice stepwise fashion. The following table shows the actual order:
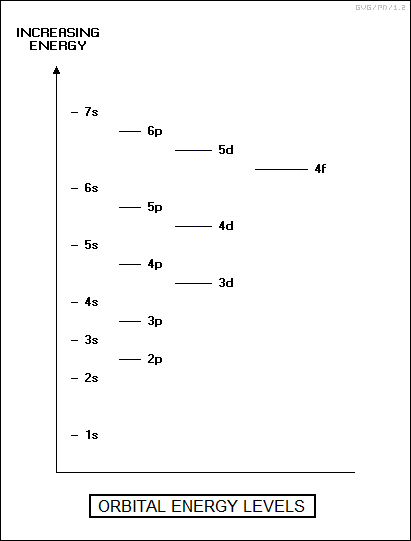
This means that orbitals are filled out as shown in the list below, reading diagonally:
1s
2s 2p
/
3s 3p 3d
/ /
4s 4p 4d 4f
/ / /
5s 5p 5d 5f
/ / /
6s 6p 6d
/ /
7s 7p ...
-- or, reading from left to right:
1s
2s 2p
3s 3p 3d
4s 4p 4d 4f
5s 5p 5d 5f
6s 6p 6d
7s 7p ...
This sequence is known as the "Aufbau order", from the German "aufbauen (to build up)". In any case, from this point on, the rules for filling up orbitals become more complicated. What is true is that all the noble gases, including those in the higher rows of the periodic table, have electron configurations which include:
ns2np6
-- providing eight electrons, and are highly stable. What is also true is that atoms in general (with many exceptions and a good deal of fine print) tend to follow the "octet rule", meaning they will form bonds to acquire eight electrons in their outermost shell.
* The fourth row of the table involves introducing the shell with n = 4 and begins with potassium (K, Z = 19), which has the ground-state electron configuration of:
[Ne] 3s1:3p6:4s1
-- or, simplifying:
[Ar] 4s1
The electron configurations of this row are built up as follows:
Z element symbol configuration
________________________________________________
19 potassium K [Ar] 4s1
20 calcium Ca [Ar] 4s2
21 scandium Sc [Ar] 3d1:4s2
22 titanium Ti [Ar] 3d2:4s2
23 vanadium V [Ar] 3d3:4s2
24 chromium Cr [Ar] 3d5:4s1
25 manganese Mn [Ar] 3d5:4s2
25 iron Fe [Ar] 3d6:4s2
27 cobalt Co [Ar] 3d7:5s2
28 nickel Ni [Ar] 3d8:4s2
29 copper Cu [Ar] 3d10:4s1
30 zinc Zn [Ar] 3d10:4s2
31 gallium Ga [Ar] 3d10:4s2:4p1
32 germanium Ge [Ar] 3d10:4s2:4p2
33 arsenic As [Ar] 3d10:4s2:4p3
34 selenium Se [Ar] 3d10:4s2:4p4
35 bromine Br [Ar] 3d10:4s2:4p5
36 krypton Kr [Ar] 3d10:4s2:4p6
________________________________________________
The properties of the elements in the fourth row of the periodic table tend to reflect the same kind of order as exhibited by the third row, with potassium and bromine being highly reactive, krypton being an inert noble gas, and gallium having an intermediate reactivity. However, the fourth row brings something new to the party, in the form of the metallic elements scandium through zinc (Z = 21 through 30). In this case, the orbital being filled up is the 3d orbital, not an n = 4 orbital; since the 3d orbital has less effect on the reactivity of these elements, they have roughly similar bonding properties.
These ten elements are called "d-transition" or simply "transition" elements; they are also sometimes called "transition metals". Technically, zinc is not a transition element, since the 3d orbital completed electronically with copper, and zinc's electronic configuration then established by filling up the 4s orbital. However, zinc's properties are similar to those of the other nine transition elements in this row and so it is usually lumped together with them, with a little fine print added to explain that this is an association of convenience.
There is one d orbital with two lobes and a ring around the connection between the lobes, and four d orbitals with four lobes, each with a different spatial orientation. Of course, each can accommodate two electrons with opposed spins.
* The fifth row of the periodic table, with Z = 37 through 54, follows the same pattern, and it is not necessary to describe it in detail. It involves filling up the 5s and 5p shells, with the row broken in the same way with ten transition elements, Z = 39 through 48, that involve filling up the 4d orbital.
The sixth row, Z = 55 through 86, repeats the pattern once more, but with a significant twist. The row involves filling up the 6s and 6p shells, with a set of ten transition elements that involve filling up the 5d shell -- but these transition elements, Z = 57 through 80, broken by 14 elements, Z = 58 through 71, that involve filling up the 5f shell. The f shell has little influence on the bonding behavior of elements, and so these 14 elements have highly similar chemical properties, making them hard to separate. They follow lanthanum (La, Z = 57) in the periodic table and are called the "lanthanide rare earths" or just "lanthanides". They aren't actually all that rare in general -- it's just that they're difficult to chemically sort out.
Incidentally, the forms of the f-orbitals are, not surprisingly, more complicated than those of preceding shells. There are three in the form of two lobes, with a ring around the lower section of each lobe, with three possible spatial orientations; and four with eight lobes, with four different spatial orientations. Of course, as usual, each orbital can accommodate two electrons with opposed spins.
The seventh row, beginning with Z = 87, matches the same pattern as the sixth, or more correctly it does to the extent that the row is populated. As explained later, as the value of Z increases above a certain level, the elements tend to break down radioactively with increasing quickness, until they cannot be formed at all. In any case, the seventh row begins by filling up the 7s shell, followed by an incomplete set of transition elements from actinide (Az, Z = 89) that involve filling up the 6d shell, with a set of 14 "actinide rare earths" or "actinides" following actinium that involve filling up the 5f shell.
* These electron structures can be summarized in an expanded periodic table that give the orbitals being filled by the elements, as well as the "groups" in which the elements are organized:
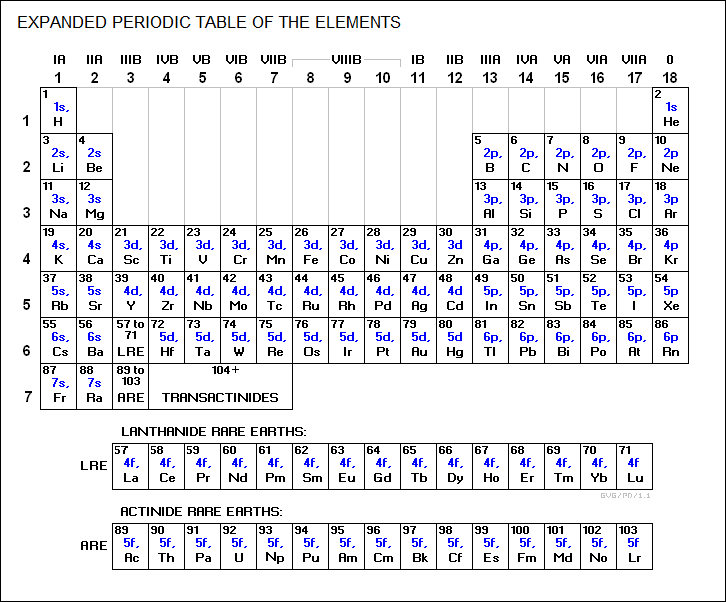
As is obvious from a quick look at the table, the elements in each group have common atomic bonding characteristics. There are "A Group elements", which are filling up s and p orbitals, and "B group elements", which are filling up d and f orbitals. The "0 group", the inert noble gases, can be regarded as a special member of the A group elements.
* It should be added that the atomic nucleus has quantized energy levels and shells as well. Maria Goeppert-Mayer (1906:1972), a German physicist who came to the US and became an American citizen, came up with the idea in a 1955 paper, published in collaboration with her colleague Hans Jensen (1907:1973) published a text on the concept in 1955 -- which won them the Nobel Prize in 1963.
The theory of nuclear energy levels is of course complicated, but a simplified model can illustrate how it relates to nuclear stability. Since both protons and neutrons are fermions, they both obey the Pauli exclusion principle, meaning that each level can accommodate only two particles, one with spin UP and the other with spin DOWN. Both protons and neutrons have their own energy levels; in this simplified model, the neutrons have equally-spaced energy levels, but due to the electromagnetic repulsion between protons the spacing between protons is greater:
proton neutron
< > < >
< >
< >
< >
< U >
< U D >
< U D > < U D > base energy level
This means that as the number of nucleons in a nucleus increases, the neutron energy levels tend to fill up more quickly than the proton energy levels. If the number of neutrons gets too far ahead of the number of protons, however, the nucleus is not at its lowest energy level, and neutrons will tend to decay into protons and electrons.
The quantum physics of the nucleus is significant in subjects such as natural and artificial synthesis of the elements, and by the same coin the natural and artificial breakdown of elements -- subjects central to nuclear power. However, that is a substantial topic that needs to be discussed elsewhere.
BACK_TO_TOP* One of the subtle consequences of the electronic configurations of the different elements is their magnetic properties. A spinning electron has a magnetic moment, meaning it acts like a little bar magnet. When two electrons occupy the same orbital, they have opposed spins and so opposed magnetic moments, and their magnetic effect cancels out. However, if an element has orbitals with only one electron, the atom inherits a magnetic moment from the unpaired electrons.
In the simplest case, in a material made up of atoms of an element with a magnetic moment, the atoms will align themselves randomly, ensuring that their magnetic moments cancel out. If a magnetic field is placed across the material and the atoms are free to move, they will align with the magnetic field, enhancing its strength. Such materials are known as "paramagnetic"; many rare earth elements have paramagnetic properties. The amount by which the material enhances the magnetic field is known as the "magnetic permeability" of the material.
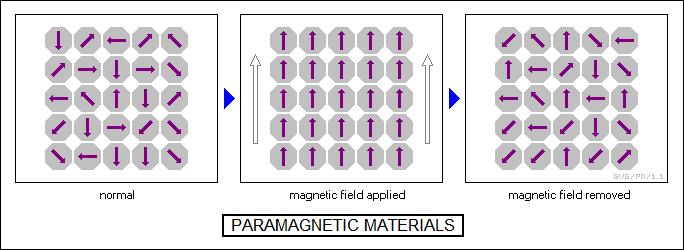
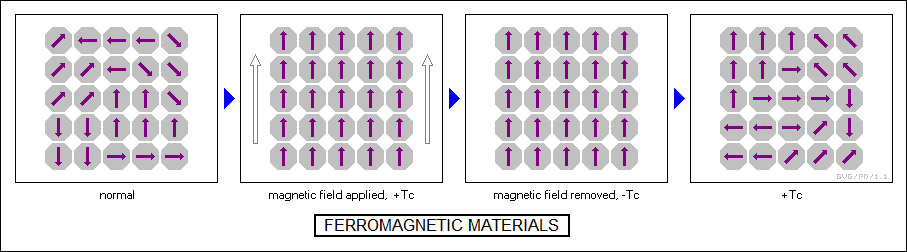
Some other atoms with a magnetic moment have a tendency to align with each other magnetically. This is due to overlap between the electron wave functions of neighboring atoms, resulting in a lower energy state if the magnetic moments of the atoms are aligned. Iron is the best-known example. Normally, the material is organized into relatively large-scale "domains" with opposed magnetic fields, and the material has little or no large-scale magnetic effect. However, if the material is heated so the atoms can reorient themselves and placed in a magnetic field, the atoms will line up; if the material is allowed to cool, the atoms will remain fixed in their orientation after the magnetic field is removed, resulting in a permanent magnet.
Such materials are known as "ferromagnetic", and they have greater magnetic permeability than paramagnetic materials. If heated again without the presence of a magnetic field, the material will fall back into domains again and lose its permanent magnet properties. The temperature at which this happens is called the "Curie temperature", after Pierre Curie, who discovered the phenomenon in 1895. Above their Curie temperature, ferromagnetic materials will change their magnetic orientation in track with changes in an external magnetic field -- but with a time lag, a phenomenon known as "magnetic hysteresis", which has some applications, but can also result in power losses.
A type of highly ferromagnetic ceramic materials, known as "ferrites" and made up of iron and boron with barium, strontium, or molybdenum, are commonly used as permanent magnets; as coatings (in powder form) for magnetic recording media; as cores in transformers, inductors, and electromagnets; and even as a component of the secret "radar absorbing material (RAM)" coatings applied to "stealth" aircraft to reduce their visibility to radar.
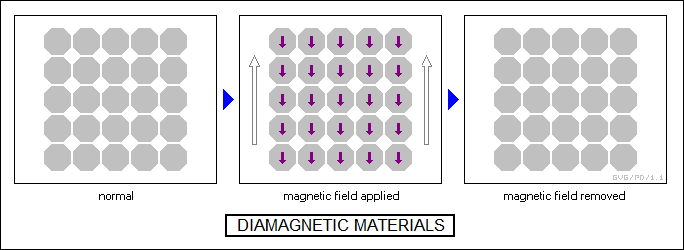
Materials made up of atoms that don't have a magnetic moment may still end up being magnetized when a magnetic field is placed across them -- but the magnetic field of the material opposes that of the external magnetic field. This property, known as "diamagnetism", is simply due to the fact that the magnetic field induces an electric current into the material, with the electric current setting up an opposed magnetic field. This is more or less straightforward "magnetic induction", very much like that which occurs when a magnetic field is placed across a loop of wire. The phenomenon is used to sort aluminum cans out of waste conveyors: while a permanent magnet won't stick to aluminum, placing a magnetic field across the conveyor belt drives the aluminum cans off of it.
* Although paramagnetism, ferromagnetism, and diamagnetism are the most common magnetic properties of materials, there are a number of specialized cases as well.
There are materials with atoms that have magnetic moments where the electron wavefunction interactions force the atoms to line up in an antiparallel fashion, aligning in a mixed and reversed pattern so that their magnetic moments cancel out. Such "antiferromagnetism" usually only occurs at fairly low temperatures; above a certain temperature, called the "Neel temperature", the couplings are broken. Below the Neel temperature, an antiferromagnetic material usually appears to be diamagnetic, normally unmagnetized but developing opposed magnetism in response to an external magnetic field; above the Neel temperature, it appears to be paramagnetic, normally unmagnetized but developing aligned magnetism in response to an external magnetic field. Antiferromagnetic materials are relatively unusual; chromium is an example of an antiferromagnetic material.
Notice the qualification of "usually" above. Some materials that are made up of two different types of atoms with different magnetic moments will line up in an antiparallel fashion just like antiferromagnets, but since the two magnetic moments don't quite cancel out, the material retains a net magnetic moment. Such "ferrimagnets" are also relatively scarce. The ancient "lodestone", a naturally occurring permanent magnet, is a ferrimagnetic material, with its magnetism created by two types of iron ions.
BACK_TO_TOP* The new tools of quantum mechanics developed in the 1920s were quickly applied to detailing chemical bonds between atoms. In 1927, two German physicists, Walter Heitler (1904:1981) and Fritz London (1900:1954), used the equation to determine the bonding in a simple diatomic hydrogen molecule (H2). This was a big first step, and the American chemists John C. Slater (1900:1976) and Linus Pauling (1901:1994) went from there to construct a full quantum-mechanical theory of chemical bonding. Pauling would get the Nobel Prize in chemistry in 1954 for this work; he was also the only person to win both a science prize and the peace prize, which he was awarded in 1962 for his anti-nuclear weapon activism.
There are several classes of chemical bonds:
Ionic bonds involve one atom stealing electrons from the other, with the resulting positive and negative ions held together by their mutual electrostatic attraction. Sodium chloride (NaCl), or common table salt, is the best-known example of a material based on ionic bonds.
Covalent bonds involve atoms sharing electrons to complete their outer shells; coordinate covalent bonds are a special case, in which the shared electrons were only provided by one of the atoms. Carbon crystals, such as diamond or graphite, involve covalent bonds. Ionic and covalent bonds aren't actually completely distinct, however, being more in the nature of two extremes. At one extreme, one atom loses electrons completely, at the other extreme they're shared equally -- but the sharing in some covalent bonds may not be completely equal, resulting in an electrically polarized molecule.
Metallic bonding, as its name suggests, only occurs in metals, and involves all the atoms of a metallic crystal sharing their electrons, in what is called an "electron gas". This electron gas has very high mobility, which is why metals are good conductors of both electricity and heat.
Hydrogen bonds are weak bonds due to the subtle polarization of molecules. A water molecule (H2O), for example, has a slight negative polarity on one side and a slight positive polarity on the other (where the two hydrogen atoms are concentrated). When water freezes, these weak bonds form up a distinctive crystal organization that makes ice less dense than liquid water, a condition not true for most other materials. Hydrogen bonds also give water a relatively high boiling point. In addition, hydrogen bonds play important roles in biosystems; for example, the three-dimensional structure of protein molecules is due to hydrogen bonding, and the two chains of the famous DNA "double helix" are joined down the center by hydrogen bonds.
* In practice, chemists use a range of models to describe chemical bonding. The simple model known as the octet rule, the tendency of atoms to share electrons to create outer shells with eight electrons, has already been mentioned. This is little more than a rule of thumb, with a large number of exceptions, but it is very handy for remembering the bonding behavior of many common elements, such as oxygen and hydrogen. Oxygen has six electrons in its outer shell and wants to have eight; hydrogen has one electron in its outer shell and wants to have two. That means that one oxygen atom can form covalent bonds with two hydrogen atoms to form water, H2O.
Slater and Pauling's work involved two associated theories, the "valence shell electron pair repulsion (VSEPR)" theory and the "valence bond" theory. They are two sides of the same coin. VSEPR simply states that the valence electrons (or pairs of electrons, when two electrons with opposed spin share an orbital) repel each other and force the bonds to be as far away from each other as possible. VSEPR doesn't specify how many bonds there are, it just specifies the bond angles as a guideline to molecular configuration. For example, the methane molecule, CH4, has four hydrogen atoms covalently bonded to a carbon atom. VSEPR dictates that the bond angles will be at the corners of a tetrahedron, and so methane is a tetrahedral-shaped molecule.
Similarly, ammonia (NH3) has a tetrahedral structure, with the nitrogen atom at one corner. It might seem more logical from VSEPR theory that it would be a flat triangle, with the nitrogen atom at the center, but nitrogen has five valence electrons, meaning that one orbital is full with two electrons of opposed spin, and these two electrons provide a repulsion that forces the three hydrogen atoms down to the corners of the tetrahedron.
Valence bond theory complements VSEPR by specifying the number of bonds and the bonding arrangement, introducing a concept known as "hybridization" that involves a "mixing" or "summing" of orbitals to set up the observed bonding arrangement. As shown by Pauling in 1931, for example, carbon has an electron configuration of:
[He] 2s2:2p2
In bonding to form methane, these orbitals are modified into four "sp3 hybrid" orbitals, with each at one corner of the tetrahedron.
Pauling also came up with the notion of "resonance". By the octet rule, an oxygen atom, which has a valence of six, can bond with two hydrogen atoms, each with a valence of one, to form the water (H2O) molecule. In a somewhat more devious way, two oxygen atoms can simultaneously steal two electrons from each other to form the diatomic oxygen (O2) molecule. However, the ozone (O3) molecule remains a bit of a puzzle to this day.
* Sometimes simplified models won't do, demanding the use of the "molecular orbital" approach, developed by Friedrich Hund and Robert S. Mulliken (1896:1986), which involves applying and solving the Schroedinger equation for an entire molecule instead of just one atom. Examples for when molecular orbital calculations might be required include computer simulations of the behavior of explosives and combustion of fuels in high-speed "scramjet" engines; design and evaluation of molecules for new drugs; and design of improved lubricants, plastics, and ultrahard materials.
As mentioned, the Schroedinger equation can't be solved exactly for atoms with more than one electron, but approximate methods can give as much precision as desired. The problem is that obtaining such precision requires immense computing horsepower. The simplest mathematical model for ethanol, grain alcohol, which has nine atoms, requires 26 mathematical functions, and each electron and nucleus in the model interacts with every other electron and nucleus. Even with modern supercomputers, molecular simulations based directly on the wave equation can be performed only on molecules up to a few hundred atoms in size.
The response has been to devise smarter, simplified strategies for modeling large molecules, sometimes using measured data to replace calculations. Other computer simulations have been devised for well-ordered materials such as crystals, using simple models such as, say, imagining the structure as a set of balls linked by springs that represent the forces holding them in balance. The latest refinement to molecular modeling is to leverage off "machine learning (ML)", a form of artificial intelligence, in which an ML system is fed molecular structures along with their properties, and learns about how properties are implied by structures. Given enough samples, then the ML system can be fed properties, and propose structures that may fit them.
Along with the modeling programs, graphics programs have been developed to allow display and manipulation of molecules, for example to examine how a particular drug molecule interacts with various biomolecules. Ultimately, computational chemists hope to be able to precisely design molecules for a particular task from the specifications for that task, but the field is still in its infancy and that sort of magic will take a great deal of effort to get working right.
BACK_TO_TOP* The invention of modern solid-state electronic devices leveraged off theoretical studies of the solid state using the new quantum physics. Solid state physics focused initially on crystalline materials, since they were more orderly and easy to analyze than amorphous materials. A knowledge of chemical bonding rules led to the understanding of the different classes of crystals, such as face-centered cubic, body-centered cubic, and other organizations, but more importantly for the topic at hand led to an understanding of the electronic properties of materials.
The most significant principle in the design of solid-state devices is the Pauli exclusion principle, obeyed by half-spin fermion particles like the electron. The exclusion principle, of course, means that that no two electrons in the same quantum system can have the same energy state. This has interesting implications when a set of such atoms is brought together in a crystal.
Since the crystal forms one big quantum system, electrons that are at the same energy state when they are components of individual atoms can no longer be at the same energy state. The result is that what was a single energy state in individual atoms becomes a broad range or "band" of energy states in the crystal, with electrons shifting up or down in energy to allow them to coexist. The energy bands of the crystal may overlap, or they may be separated by "forbidden regions" or "bandgaps" where there are no possible energy states. It is the spacing of the energy bands and the bandgaps that help explain the electronic behavior of the solid.
At absolute zero, the electrons in the crystal will all be in their minimum energy states. The maximum occupied energy state in this circumstance is called the "Fermi level" or "Fermi state". If the temperature is raised, electrons will move to higher energy states -- if they are able. If the Fermi level lies in the middle of an energy band, then there is no obstacle to increasing the energy level of the electrons. A material with such an arrangement is highly conductive, in both the thermal and electronic sense. Such a crystal tends to absorb light, since the electrons can be excited by incident photons, and so are generally opaque. Good examples of crystalline "conductors" are metals such as copper, gold, silver, and aluminum.
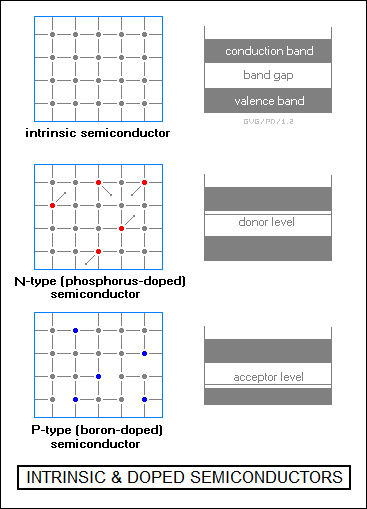
If the Fermi level is at the very top of an energy band, the electrons in this "valence band" -- named because it is the outermost or valence electrons that occupy this range of states -- have to be given enough energy to jump up over the bandgap into the neighboring higher "conduction band" in order for them to become mobile, or in other words act as "charge carriers". If the bandgap is large, electrons tend to stay in the valence band, and the crystal has poor thermal and electronic conductivity. It also tends to not absorb light and be transparent. Good examples of crystalline "insulators" are quartz and diamond. However, if the bandgap is relatively small, the material has properties intermediate between those of a conductor and an insulator. Such materials are "semiconductors", with the best-known example of course being silicon.
* Pure or "intrinsic" silicon isn't all that useful in itself. Heat and light will cause electrons to jump from the valence band to the conduction band, and so intrinsic silicon can be used for temperature or light sensors. Its behavior becomes more interesting if impurities are added to the crystal structure of silicon.
Silicon has a valence of four, typically forming four bonds. In a silicon crystal, these are purely covalent bonds, with each silicon atom linked to four neighbors in a tetrahedral structure, though the structure can be modeled more simply if less accurately in a two-dimensional structure that consists of a nice rectangular grid of silicon atoms.
Now suppose a trace of phosphorus atoms is introduced or "doped" into this nice neat crystal matrix. Phosphorus has a valence of five, so a phosphorus atom adds a "dangling" bond into the matrix. The end result is that this frees up electrons to act as charge carriers, and the conductivity of the silicon is greatly increased. From the more abstract point of view of band theory, the presence of the phosphorus introduces a new set of states in the bandgap, just below the conduction band.
Next, suppose a trace of boron atoms is doped into the silicon matrix instead of phosphorus atoms. Boron has a valence of three, and so its introduction into the matrix leaves silicon bonds dangling. This also increases the conductivity of the silicon. From the point of view of band theory, the presence of the boron introduces a new set of states in the bandgap, just above the valence band.
On a per-atom basis, boron doesn't contribute as much to conductivity as much as phosphorus does. Imagine as a very rough analogy the intrinsic silicon matrix as a flat box loaded with billiard balls that are packed so tightly that they can't move around. Adding phosphorus to the matrix is like throwing more balls on top of the box, and these new balls can move around very easily. Adding boron to the matrix is, in contrast, like removing some of the balls from the box; the remaining balls can shift around, but not as efficiently. Interestingly, what appears to be moving around in this case is not the balls themselves but the "holes" left when the balls were removed, and so the charge carriers in silicon doped with boron are called "holes". This is obviously less efficient and so the "charge carrier mobility" is lower. This analogy can't be pushed too far: it's strictly mechanical, while in the case of doped silicon what's being shuffled around are electrons and available energy states.
In general, valence-five atoms like phosphorus are called "donor" impurities, since they "donate" electrons, and the resulting altered silicon matrix is known as "N-type" silicon. Valence-three atoms like boron are called "acceptor" impurities, since they "accept" electrons (creating holes), and the resulting silicon matrix is known as "p-type" silicon. It must be emphasized that in either case, the matrix is electrically neutral: the number of protons equals the number of electrons. The only thing that has been done is to tinker with the crystal structure to improve the mobility of charge carriers.
Microcircuits are fabricated using something like microscale silk-screening, creating n-type and p-type regions in a wafer of otherwise pure silicon, with silicon dioxide -- glass, really -- being used as an insulator, and a network of metal traces and contacts overlaid for connections. The end result is a system of electronic switches, "transistors", that turn on and off, switching electrical currents in response to electrical inputs.
There is far more to the manufacture of semiconductor devices than this. Indeed, in the decades following World War II, research into the solid state expanded in range, covering not merely crystalline substances but also amorphous materials such as glasses, as well as liquids. Obviously, the term "solid state physics" was hard to apply to liquids, and so a new umbrella term, "condensed matter physics", was invented. Again, it's a big subject that needs to be discussed elsewhere.
BACK_TO_TOP