* The probabilistic interpretation of the Schroedinger wavefunction made many physicists uneasy, but their discomfort was only beginning. Werner Heisenberg would add to it by describing the "uncertainty principle", which imposed a limit on how precisely a subatomic "quantum" system might be observed. Niels Bohr raised the discomfort to a higher level by helping construct the "Copenhagen interpretation", which asserted that as far as quantum systems were concerned, nothing could be said about existence until the system was observed.
* Bohr was cautious about committing to Born's probabilistic interpretation of the electron wavefunction. He kept an open mind on the matter, discussing it with Heisenberg and Pauli in Copenhagen through much of 1926 and into early 1927. Heisenberg had not forgotten about the strange inequality he had discovered in matrix mechanics:
p * q - q * p = ( Planck's_constant / 2PI ) / i
During this period he began to think more about the implications, engaging in conversations with his colleagues on the matter. Pauli's critical abilities were particularly useful for this purpose, and he and Heisenberg had become close collaborators. Working with Pauli, Heisenberg became convinced that the inequality was no mere mathematical artifact. The conclusion was that in the quantum realm there were pairs of parameters -- such as the position and momentum of a particle -- that were linked together in such a way that obtaining a better value of one meant obtaining a poorer value of the other. More specifically, the product of the range of uncertainty, or "delta", of the position of a particle and the delta of its momentum was never less than hbar:
delta_position * delta_momentum >= hbar
As noted earlier, the dimensions of an electron were found to be absolutely minimal, and it is this uncertainty relation that defines these absolute minimum dimensions, giving a limit to how small an electron can be considered to be. The energy of a particle and the interval of a measurement have a similar relationship:
delta_energy * delta_interval >= hbar
Not so incidentally, by definition the concept of the "delta" only makes sense for large numbers of measurements. If we make a single measurement of, say, the position and momentum of a particle, we can get nice crisp specific values of both. However, to determine the validity of that measurement, we have to perform the same measurement again, and as we perform a series of such measurements, we infuriatingly find that the range of values of position and momentum dance around to the extent that their product will never be less than Planck's constant.
What the Heisenberg "uncertainty principle" implied was that if we obtain a perfect knowledge of the position of an electron, then we have no way of knowing its momentum, and the reverse. It also reinforced Born's probabilistic interpretation of the electron wavefunction, since if it was impossible to precisely define the momentum of the electron, then its position could only be determined in terms of probabilities. Position and momentum, or energy and interval, are known as "conjugate" quantities. By the way, not all the parameters of quantum entities such as the electron are subject to the uncertainty principle: for instance, the mass of the electron is a known quantity, and all electrons have exactly the same mass.
The uncertainty principle is inherent in quantum physics. In the view of quantum physics, a particle is regarded as a "wave packet", a short bundle of waves. In classical wave analysis, any periodic waveform -- a square wave, a triangle wave, and so on -- can be regarded as a sum of a sequence of pure sine waves of different amplitudes, wavelengths, and phases. This is known as a "Fourier series" and the set of sine waves is referred to as a "Fourier spectrum".
As the pulses in a periodic waveform are spaced out, the Fourier spectrum becomes more crowded with elements, until in the limit of a single pulse the spectrum become a continuous "Fourier integral". A wave packet is described by a Fourier integral; since the properties of a particle are determined by its wavelength, the dispersal of wavelengths implied by the wave packet's Fourier integral also implies a dispersal of the particle's properties that cannot be reduced. One of the features of a Fourier integral is that as the width of the wave packet is reduced, the integral becomes wider, which exactly matches the circumstances of the uncertainty principle.
Incidentally, the uncertainty principle explained, sort of, why the electron didn't spin at ten times the speed of light. Although the electron had been seen as a point particle, the uncertainty principle set a bound on how closely the position of that point particle could be pinned down. This bound could be regarded as the measurable diameter of the electron. This diameter could also be visualized as that of a spinning particle, and analysis showed that the spin rate did not exceed the speed of light.
* Heisenberg had another angle on the uncertainty principle. In the macroscale world of classical physics, performing a measurement on an object does not affect it in any serious way. For example, we can use radar to obtain the position and velocity (effectively the same as the momentum) of an aircraft, by the conceptually simple means of sending out directional pulses of radio waves and then measuring the time delay for the return of their reflections from the aircraft. Although the radio waves do carry some momentum that is transferred to the aircraft when they are reflected, that momentum is so slight that the position and velocity of the aircraft are not changed in any measurable way.
Heisenberg imagined a "quantum microscope" that observed particles such as electrons by bouncing photons off of it. Of course, such particles are far smaller than aircraft, and so photons of much shorter wavelength are required to track it -- as the target grows smaller the appropriate photons must in the visible, then ultraviolet, then X-ray, and finally gamma-ray regions of the electromagnetic spectrum. As the wavelength decreases, the photons become increasingly effective in determining the position of the particle. However, the energy and momentum of the photons increases as well, and at gamma-ray wavelengths the photons effectively knock the particle completely out of the ballpark. In attempting to measure the position and velocity (momentum) of the electron, we are inescapably changing its position and velocity.
The concept of the quantum microscope remains part of the story of quantum physics, and in fact many books present it as the only rationale for the uncertainty principle. However, the uncertainty principle is inherent in the wave packet nature of quantum entities, and the quantum microscope thought experiment is hobbled, though not completely wrecked, by a significant flaw: it assumes that there really is a particle, in the sense of a tiny ball, present. Bohr criticized this notion so relentlessly that it is said Heisenberg was reduced to tears.
BACK_TO_TOP* Bohr had spent a great deal of time and effort thinking about the implications of quantum physics, and following a vacation in February 1927 he finally managed to put it together. In Bohr's view, the uncertainty principle meant there was no way to tell if the electron really was a tiny ball, and it was even nonsense to suggest that it was. In fact, according to Bohr any visualization of an electron was nonsensical -- there's no way to see in a visual sense an electron, we can just measure its properties and effects -- and instead of calling an electron a particle it was really more appropriate to give it the vague title of "quantum entity". This is a somewhat clumsy phrase and the modern physicist Nick Herbert (born 1936) invented his own word for it, "quon", but it didn't catch on.
Bohr had, in his usual persistent way, engaged in long discussions with his Copenhagen group to come up with a scheme for dealing with the quandaries created by quantum physics. The scheme would become known, not too surprisingly, as the "Copenhagen interpretation".
It is difficult to find consistent descriptions of the Copenhagen interpretation, mostly because Bohr never described it in a complete way, and also because he was not a particularly clear writer. One element was what Bohr named the "complementarity principle", a rule he devised to help deal with the notion of wave-particle duality. The complementarity principle stated that an experiment to demonstrate the wave nature of a quantum entity -- a photon, an electron, an atom, a buckeyball molecule -- would show it was a wave, while an experiment to demonstrate its particle nature would show it was a particle.
That in itself is not too hard to swallow, but the implications are dizzying. Consider the classic two-slit interference experiment, in this case conducted with photons -- though as far as this argument is concerned, any other quantum entity works the same. If a light beam is focused on two slits, it builds up an interference pattern of light and dark lines on the screen beyond.
Now suppose we fit detectors to one or both of the two slits to determine which slit a particular photon goes through. If we do this, then the interference pattern disappears: there's a bright region behind each slit but not elsewhere, which is exactly what would be expected if light were made up of classical particles. In addition, if a sensor is set up to detect photons after they go through the slits, the photons will also appear as particles, with no interference effect. It's as though they were able to detect in advance whether they were supposed to act as a particle or a wave.
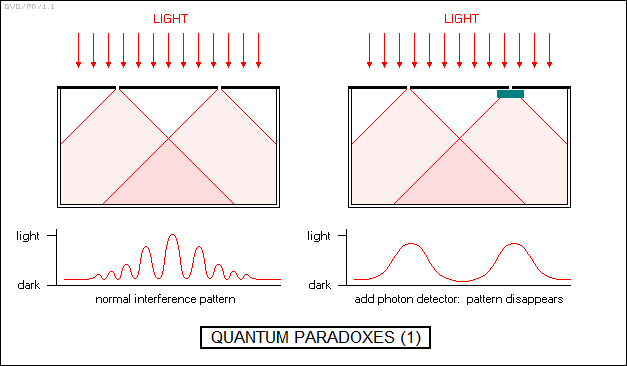
What is particularly perplexing is that modern tests of the two-slit interference experiment conducted by firing one photon (or other quantum entity) at a time at the slits gradually builds up the interference pattern. What is each photon interfering with? It's as if it goes through both slits at once and interferes with itself. As baseball great Yogi Berra once put it: "When you come to the fork in the road, take it." Adding the fact that the interference doesn't happen if the photons are observed going through one or both slits makes it even more baffling: "Nobody's looking -- let's go for it."
Much the same thing happens if a light beam is passed through a tiny hole: it will produce an interference pattern composed of concentric rings. If the photon flow is choked down until it is reduced to a single photon every now and then, the interference pattern still gradually appears. If a detector is fitted to the hole to count the photons going through, the interference pattern disappears.
None of this makes any sense in terms of classical physics. As far as anyone can determine, an individual photon is a point particle, with no wavelike properties at all. To be sure, a water wave is made up of individual particles, water molecules -- but there's absolutely no way that an intermittent stream of single water molecules looks anything like an ocean wave. Photons, in contrast, seem to "know" that they are being built up into a wave interference pattern.
Nobody argues this phenomenon. It may seem completely unreasonable, but that's the way it's been observed to work. Nature does whatever it does, and we have no choice but to follow along, as guided by our observations. Nobody has ever done the experiment and obtained different results. The great American physicist Richard P. Feynman (1918:1988 -- pronounced "Fine-man", by the way), one of the most colorful characters to ever take up physics for a living, said it was "the central mystery" of quantum physics, even "the only mystery" of quantum physics. As far as all other quantum paradoxes went, Feynman always felt he could answer: "You know the two-slit experiment? They're all basically like that."
The Copenhagen interpretation gave a very strict reading of the probabilistic interpretation of the Schroedinger wavefunction. In the probabilistic interpretation, any quantum entity could only be defined by its wavefunction -- a probability distribution -- until it was observed, with the observation producing specific measurement values. As noted earlier, the square of the Schroedinger wavefunction gave the probability of detecting a particle at a particular location; however, that was all it gave. In this view, it was absolutely not correct to think that before the wavefunction was measured, there was a particle "hiding in it" somewhere. Before observation, all that could be said was that there was a set of probabilities; nothing else was defined. The uncertainty principle said that was the best anyone could do.
In the two-slit experiment, according to the Copenhagen interpretation, as the photon (or other quantum entity) passed through the experimental apparatus, its only existence was as a probability function, with no values of that function ruled out; it existed only as a potential to become one of all its possible values, a condition known as a "superposition of states". When it was finally observed, the wavefunction "collapsed" into a definite value, a process named "decoherence".
Superposition of states -- the notion that, say, an electron has a value of both spin +1/2 and -1/2 until it is observed -- and the concept of decoherence are not argued, either. When a student of Feynman's said he didn't believe it, Feynman replied: "Well, go do the experiments until you DO believe it."
Superposition of states can be demonstrated by a simple experiment. One of the demonstrations of light polarization involves taking two polarized lenses in series and rotating on at a right-angle orientation to the other. This blocks out all the light, as would be expected in classical physics. However, if a third polarizing lens is placed between the two other lenses and rotated only 45 degrees, then about a quarter of the light will pass through the entire lens assembly.
This happens because a polarization filter does not only pass photons in its plane of polarization: it has a probability of passing photons with decreasing probability with the angle away from the plane of polarization, until at 90 degrees the probability goes to zero. With two filters at right angles, this will indeed shut off all the light; but inserting the intermediate filter at 45 degrees introduces a second probability distribution for polarizations from the photons passed by the first filter, and the effect of the two probability distributions is to allow photons to pass through.
* These bizarre observations were bad enough. The Copenhagen interpretation placed them in a certain framework that many found exasperating or infuriating. As Bohr put it: "There is no quantum world. There is only an abstract physical description. It is wrong to think that the task of physics is to find out how nature is. Physics concerns what we can say about nature."
Bohr understood that, in the quantum realm, all we had were measurements, and any model we made simply provided a framework to fit the measurements together. As far as he was concerned, Heisenberg was on the right track in making up matrix mechanics, coming up with a set of rules that defined what should be observed without bothering to worry about visualizing how it worked -- because that couldn't be done. It wasn't really a new idea; when Isaac Newton proposed the law of universal gravitation, he just described how it worked, not why it worked, saying: "I frame no hypotheses."
The Copenhagen interpretation insisted that the quantum entity was indeterminate, undefined until it was observed; the uncertainty principle implied that nothing more could be said about it, even in principle. As the well-known modern physicist John Archibald Wheeler (1911:2008) put it: "No phenomenon is a real phenomenon until it is an observed phenomenon."
To compound the bafflement, the question of what constituted an "observation" was hard to define: did it mean an observation only by a conscious being? Couldn't that be construed as saying -- as the brilliant Hungarian-American mathematician John (Janos) von Neumann (1903:1957) cautiously pointed out in a book on quantum mechanics published in 1932 -- that reality only came into being because of consciousness? If so, did anything really exist before the rise of consciousness?
Wheeler said as much, though he may well have been simply throwing out ideas; others more sarcastically suggested that the only proper observers were those with a doctorate in physics. In reality, the question is less one of "observation" than of "observability": once we reach the limits of observation as imposed by the uncertainty principle, we have to take the unsettling rules of the quantum Universe into account.
Certainly, the idea that the Universe was created by consciousness was more than the common-sensible Bohr was willing to swallow -- sane humans are literally incapable of sincerely doubting the existence of objective reality independent of our minds, anybody who honestly didn't believe it would not be long for this world -- and it certainly was a trite observation that there were no observations without an observer. Bohr still understood quantum physics was a hard sell, observing: "Anybody who is not shocked by the quantum theory has not understood it." He also realized that he was wading in muddy waters, providing as a parable lectures given by a famous rabbi:
BEGIN QUOTE:
The first talk was brilliant, clear and simple. I understood every word. The second was even better, deep and subtle. I didn't understand much, but the rabbi understood all of it. The third was by far the finest, a great and unforgettable experience. I understood nothing and the rabbi didn't understand much either.
END QUOTE
BACK_TO_TOP* Bohr outlined the ideas of the Copenhagen interpretation at the Fifth Solvay Conference on Physics in October 1927. The first Solvay Conference had been held in 1911; it had been organized by an eccentric Belgian industrial chemist named Ernest Solvay (1838:1922), who had developed an important industrial chemical process and become very wealthy off of it. Solvay liked to dabble in physics and come up with his own theories, none of which amounted to much, but since he was rich physicists were inclined to humor him. Their patience paid off dividends when one physicist suggested to Solvay that he should set up a conference of the greatest minds in physics, so he could present his theories to them. Solvay could not resist such an appeal to his egotism, and the physics community benefited from it.
Most of the audience at the Fifth Solvay Conference accepted the Copenhagen Interpretation: a new generation of physicists had emerged that were open to such new ideas and were not upset by them. However, Einstein and Schroedinger refused to buy it.
The view of classical physicists towards their theories is best summed by Einstein's example of a clockwork pocket watch. It can be observed that the watch is wound up, and then turns the hour, minute, and second hands around the clock face. It can be inferred that:
In terms of classical physics, this analysis actually allows us to understand a great deal about the inner workings of the watch without even opening it up. Bohr's attitude was basically that this was fine for a watch, but it had no relevance for an analysis of events at the quantum level. The most that can be done is to perform experiments and write down the results. Bohr insisted that the uncertainty principle meant that nothing could be said about the inner workings of the watch.
Erwin Schroedinger mocked the Copenhagen interpretation with a well-known thought experiment concerning a cat sealed in a box, along with a vial of deadly cyanide gas. The vial could be opened by a trigger mechanism that was activated by the decay of a radioactive material. Since radioactive decay was a quantum process, the cat's survival was directly linked to a quantum process. Schroedinger said that, according to Bohr's views, until the box was opened the cat was neither really alive nor really dead: it was in a superposition of states, both completely dead and fully alive. This notion was inherent in the probabilistic interpretation of the wavefunction, since it implied a squaring of an entire function -- that is, it implied:
(X + Y)^2 = X^2 + 2 * X * Y + Y^2
-- not:
X^2 + Y^2.
The notion of a "half-dead cat" sounds absurd -- that's how Schroedinger wanted it to sound -- and very few could or would seriously argue that there was a half-dead cat in the box. Schroedinger had posed a difficult question to proponents of the theory, basically asking them: OK, explain why not? Superposition of states was experimentally provable; where was the dividing line between the ghostly microscopic quantum world of photons and electrons, and the concrete macroscopic world of cats?
Einstein believed, as his story about deducing the inner works of a watch revealed, that physics should be equally able to understand the inner workings of the Universe. He could not believe that it was, as far as the quantum world went, an impossibility. During the 1927 Solvay Conference, Einstein came up with refutation after refutation of the Copenhagen interpretation. He would present them at breakfast, and Bohr would then become uncharacteristically excited and spend the day walking around in an abstracted fashion, mumbling "Einstein ... Einstein ... " to himself. At dinner, Bohr would reply and blow Einstein's refutation out of the water. One of Einstein's friends, Paul Ehrenfest, scolded Einstein for his conservatism: "I am ashamed of you. You put yourself in the same position as your opponents in their futile attempts to refute your relativity theory."
Bohr walked away unscathed by Einstein's jabs at the Fifth Solvay Conference, but Einstein wasn't done with the matter, taking a particularly heavy shot at it at the Sixth Solvay Conference in 1930. Einstein visualized, in yet another one of his many "thought experiments", a sealed box with a shutter that contained a "gas" of photons and a clock that would open the shutter at a specified time to let precisely one photon out. The box would be weighed before and after the release of the photon. Since by Einstein's famous relation:
E = M * C^2 M = E / ( C^2 )
-- mass was equivalent to energy, the difference in the mass of the box would give the energy of the photon. Since the clock let the photon out at a specified time, then the uncertainty relation:
delta_energy * delta_elapsed_time >= hbar
-- was broken by this experiment.
Witnesses said Bohr reacted initially with shock and then with great excitement. He worried that Einstein had in fact struck a vital blow against quantum physics. Bohr, in a fever, considered objection after objection, rejected them all, and then, worn down, went to bed. The answer came to him in the night. Einstein's theory of general relativity stated that time slows down in a gravity field: a clock in a strong gravity field runs more slowly than one in a weak gravity field. Bohr pointed out that the momentum of the released photon gave the box a bit of "kick" from recoil that adjusted its position slightly. That meant that the position of the clock in the gravity field was uncertain, which further meant the time the clock was keeping was uncertain -- uncertain enough so that the Heisenberg uncertainty relation was not violated.
Einstein finally admitted that quantum physics was correct, but continued to insist that it was not complete, that it was missing something. It just didn't feel right, and he continued to press this issue in a lifelong series of friendly debates with Bohr. Still, he was willing to admit that he might be fighting a losing battle. Late in his life, after reading a paper on quantum mechanics written by Richard Feynman, Einstein commented: "I still don't believe that God plays dice ... but maybe I've earned the right to make my mistakes."
John Wheeler -- who seemed perfectly sober, often reminding people of a banker, but was a bit of a sly prankster -- later poked some good-natured fun at Einstein over quantum physics. Wheeler was a neighbor of Einstein's in Princeton, and had a cat that for reasons known only to itself chose to include Einstein's house in its turf; Einstein was always bringing the cat back to Wheeler's house. Wheeler suggested that this scenario provided a quantum-mechanical parable along the lines of Schroedinger's Cat. Schroedinger's Cat was half-alive, half-dead; Wheeler's Cat was in two places at once -- a neat trick, even for a cat.
* Anyway, Einstein was seen as being on the wrong side of the facts, since the Copenhagen interpretation overwhelmed all opposition. At the Fifth Solvay Conference in 1927, Louis de Broglie had offered an alternative interpretation, suggesting that the Schroedinger wavefunction was a real physical function that guided actual particles on a definite path. In fact, Newton had foreshadowed such a concept centuries before: although Newton believed that light was a particle phenomenon, he did observe interference effects in a shallow lens sitting on a flat mirror, and suggested that wave effects of some sort were associated with the passage of light particles.
De Broglie's paper was the grandfather of what are now known as "hidden variable" quantum interpretations. Unfortunately, his ideas were too vague to stand up to the relentless hammering of the Copenhagen clique. In fact, in his 1932 book on quantum mechanics von Neumann published a "proof" that ruled out hidden variable interpretations. Such was the momentum of the Copenhagen interpretation and the reputation of von Neumann that when the German mathematician Grete Hermann (1901:1984) pointed out in 1935 that the "proof" contained a blatant and devastating fallacy, she was simply ignored, though her criticisms would be validated decades later.
There are those who claim the Copenhagen interpretation set physics back for decades -- some saying it wasn't really an interpretation, it was more a denial of interpretations. It didn't really answer any of the questions, it simply gave a framework that allowed scientists to shrug them off and move on. It was a "don't worry be happy", or at least "don't worry", attitude.
The response was: who needed more? At the limits of observation, asking WHY the quantum world behaved the way it did was futile, since no lower level of detail could be observed. It was just the way things were, and no amount of worry over that fact would render them much more explicable.
For all the debate, the revelations of the "new quantum theory" -- matrix mechanics, wave mechanics, the probabilistic interpretation of the wavefunction, the exclusion principle, and the uncertainty principle -- were a true revolution in physics. They all took place over a very short period of time, from January 1925 to January 1928.
BACK_TO_TOP* The development of quantum physics gave physicists highly effective tools to understand the atom and the subatomic world, which would be put to literally world-shaking use. By the 1920s, it was known that atoms had subordinate particles, in the form of electrons and protons; knowledge of the atom suggested there was a neutral particle as well. The neutral particle, of course named the "neutron", was finally discovered by the British physicist James Chadwick (1891:1974) in 1932, with Chadwick winning the Nobel Prize for the discovery in 1935.
The neutron was hard to pin down because neutral particles, with no electric charge, can effectively only be detected through collisions with particles that do have an electric charge. The neutron proved to be very slightly heavier than the proton, by about 0.14%, with a mass of 1.675E-27 kilograms. Incidentally, protons and neutrons are collectively referred to as "baryons".
The model that emerged of the atom represented it as made up of a nucleus composed of protons and neutrons, surrounded by orbitals of electrons. A particular atomic element, it turned out, has a specific "atomic number" of protons -- iron, for example, has 26 protons. However, the number of neutrons may vary, resulting in "isotopes" of a particular element with different "atomic weights" -- stable isotopes of iron, for example, may have 28, 30, 31, or 32 neutrons, giving atomic weights of 54, 56, 57, and 58 respectively.
Protons each have a positive electric charge, so they repel each other, making it a puzzle as to how an atomic nucleus stays together. In 1932, Heisenberg suggested the existence of a short-range "strong force" associated with the neutrons. Since, as atomic number increases, the long-range repulsive forces between the protons make the nucleus more unstable, more neutrons are needed to hold the nucleus together with their short-range attractive force, meaning the ratio of neutrons to protons increases with atomic number. The nucleus also generally becomes more unstable with atomic number, either fragmenting spontaneously in radioactive decay, or easily breaking apart from an impact of another particle. It is no coincidence that the strong force is about a hundred times stronger than the EM force, and that the heaviest stable nuclei has an atomic number of a little under a hundred.
The hunt for the neutral neutron was paralleled by a hunt for particles with reversed electric charge -- that is, electrons with a positive charge and protons with a negative charge. In 1931, Dirac postulated the existence of such particles, which he named the "anti-electron" -- later "positron" -- and "anti-proton". He further suggested that if a particle encountered its anti-particle, the two would be annihilated; if an electron ran into a positron, the two would disappear and be converted into gamma rays. Gamma rays might also collide and produce an electron and positron, a scheme known as "pair production".
Taking a broader view, Dirac believed there was an "antimatter" that mirrored matter. Antimatter would appear almost completely like normal matter, but if it came into contact with normal matter, the two would annihilate each other in a tremendous burst of energy produced by complete mass-energy conversion.
The discovery of the neutron also led to a better consideration of the process of "beta decay", in which a neutron decays into a proton and an electron. In 1934, Enrico Fermi described a process by which it could occur, tracing it to what became known as the "weak force" -- not exactly a force as most layfolk would understand it, its only particularly visible manifestation being beta decay.
In describing the decay process, Fermi postulated the existence of a neutral particle that was massless, or nearly so, naming it the "neutrino". There was skepticism over his proposal, since the neutrino would be "weakly interacting", able to pass through light-years of lead like it was nothing. However, the neutrino would eventually be discovered.
Of greater significance in the short term, in 1934 the Austrian physicist Lise Meitner (1878:1968) managed to "split the atom", breaking apart uranium atoms with neutron bombardment to produce, among other things, an isotope of barium. Breaking apart a nucleus implied breaking the bonds of the strong force that held the nucleus together, the result being a small loss of mass in the end products, the deficit being manifested as energy.
That, according to Einstein's classic E=MC^2 equation, could mean a lot of energy, if there were only some way to "mass produce" the fission of atoms. It was Leo Szilard (1898:1964) -- a Jewish Hungarian physicist who had fled to Britain after being driven out of Germany in 1933 -- who figured out it might be done. While walking the streets of London in 1934, Szilard realized that the key was a "chain reaction": the fission of one atom by neutrons releasing more neutrons to perform fission on other atoms, leading to a cascade that released a vast amount of energy.
Szilard eventually made his way to the USA, as did Enrico Fermi. With the outbreak of war in 1939 Szilard, Fermi, and other physicists began to press the US government to set up a program to develop the atomic bomb. Although there was considerable skepticism -- atomic bombs were stuff of science fiction at the time -- the US government did set up the Manhattan Project to successfully build the atomic bomb. In the postwar period, continued research on the atom led to the construction of fission reactors for power generation, as well as fusion weapons.
Along with unlocking atomic power, the quantum revolution also radically changed chemistry. While the old rules-of-thumb that chemists used to assess chemical bonding necessarily remained in widespread use, the Schroedinger equation gave a vastly more exacting model of atomic and molecular structures. In addition, work during the war also led to an understanding of the quantum physics of solids, leading to the emergence of the solid-state electronics era, and the digital electronics era that came out of it.
BACK_TO_TOP