
* Prewar work on a quantum theory of electromagnetism had been stalled by theoretical difficulties and then the distraction of World War II. After the war, the work of Dick Feynman and others led to the construction of a (mostly) satisfactory theory of "quantum electrodynamics (QED)", which would become the model for quantum theories of other forces. It also led to the concept that the vacuum itself is full of energy, though the idea of "zero point energy (ZPE)" is still hotly debated.
* Heisenberg's proposal that there was a strong force holding together the nucleus raised the question of how the strong force worked. The neutron obviously had something to do with it, but what? He suggested that the protons and neutrons in a nucleus were impermanent: a neutron could pass an electron to a proton, with the neutron then becoming a proton and the reverse. This process would be going on at a great rate at all times, and the net effect would be a strong attractive force. However, neutrons, protons, and electrons are all spin-1/2 particles, and so that implied that either the spin was magically created out of nothing, or that these electrons were spin-0 particles. Few were enthusiastic about Heisenberg's speculations.
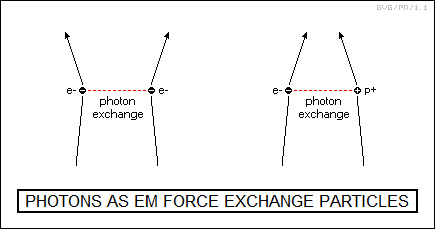
However, other options were available. In the late 1920s, Paul Dirac had been working on the Schroedinger equation, revising it to be compatible with Einstein's theory of relativity. The "Dirac equation", as it was known, was a superset of the Schroedinger equation that reduced to the Schroedinger equation when the velocities of particles in the system being described were low. Dirac then used that work as a springboard for consideration of origins of the electromagnetic field in a quantum context. Quantum mechanics asserted that electromagnetic energy was carried in discrete packets, the photons; that implied, as Enrico Fermi and others pointed out, that the electromagnetic field, which set up a force between two charged particles, actually amounted to exchanges of photons between those two charged particles.
The photon was the "exchange particle" that mediated the electromagnetic force. These photons were created even though the energy to produce them wasn't present. This violation of energy conservation was permitted because the Heisenberg uncertainty relation:
delta_energy + delta_time >= hbar
-- provided a dodge: a particle of a given energy could be spontaneously produced, but only as long as it didn't live long enough to be detected. Of course, the higher the energy, the shorter the time of its existence. Such photons were called "virtual particles".
It is intuitive that two charged particles could generate a repulsive force by bouncing photons off of each other, but Dirac's analysis showed that they could generate an attractive force as well. This being counterintuitive, photons sometimes called "messenger particles" instead of exchange particles, on the rationale that they send a "message" between two charged particles to tell them to fly apart or to come together.
The shy, brilliant Japanese physicist Yukawa Hideki (1907:1981) began to tinker with the notion that the strong force might also involve an exchange of particles. Yukawa initially suspected that the force that held the nucleus together was mediated by rapid exchanges of photons, just as photons mediated the electromagnetic field. The problem with this idea was that a strong force based on photon exchanges would have been detectable outside of the nucleus, and the strong force was not: it clearly only worked at the very close ranges inside the nucleus. Electromagnetism and gravity fall off in an inverse-square fashion -- double the distance and the force is reduced by a factor of four -- but the supposed strong force clearly fell off very rapidly. If gravity behaved in the same way, we could become weightless by walking up the stairs of a building.
The photon is the mediating agent of the electromagnetic field, and physicists believe that the gravitational field is mediated by a particle as well, named the "graviton", though its action is so subtle that it has never been detected. These particles are massless, travel at the speed of light, and nothing interferes with their motion through free space; simple considerations of geometry lead to their inverse-square range law. Yukawa believed that the short range of the strong force could be explained if the exchange particle was massive.
Yukawa's exchange particle was a virtual particle, governed by the Heisenberg uncertainty relation:
delta_energy + delta_time >= hbar
Since, according to Einstein's theory of relativity, nothing could exceed the speed of light, the amount of time Yukawa's particle could exist could be no more than the range of the strong force divided by the speed of light. Plugging this into the relation gave:
delta_energy + range_strong_force / speed_of_light >= hbar
This gave the minimum energy of Yukawa's particle as:
delta_energy = hbar - range_strong_force / speed_of_light
By Einstein's mass-energy equivalence E = MC^2, the delta_energy meant a particle about 15% as massive as the proton, or 200 times more massive than the electron. This particle would be exchanged between nucleons, changing protons to neutrons or the reverse.
Photons are massless, and so people could swallow their "virtual" creation and absorption by charged particles. The idea of Yukawa's large particles being created and absorbed by nucleons on a continuous basis seemed a bit more of a stretch. However, the real problem with Yukawa's theory was that nobody knew of any such particle at the time, leading him to suspect he was on the wrong track, but he went ahead and published his results anyway in 1935. If he was wrong -- well, maybe somebody would be able to tell him where his blunder was.
At first, the reaction of the physics community to his ideas was indifferent at best, critical at worst; on a visit to Japan, Niels Bohr told Yukawa: "You must like to invent particles." Indeed, a Swiss physicist named Baron Ernst C.G. von Stueckelberg (1905:1984) came up with much the same theory in parallel, but Wolfgang Pauli savaged the idea so badly that Stueckelberg didn't bother to publish.
Yukawa wouldn't be vindicated until after World War II. In the 1930s, the British physicist Cecil Frank Powell (1903:1969), of Bristol University, had developed a new technique for obtaining the tracks of charged particles, using stacks of photographic plates. In 1947, Powell observed the tracks of an unstable charged particle in stacks of plates sent to mountaintop observatories. It had a mass 273 times that of the electron, and strongly interacted with protons and neutrons; it was obviously Yukawa's exchange particle, being named the "pi meson" or "pion".
Three variants were found, with the negatively-charged "pion-" and "pion+" discovered initially and the neutral "pion0" discovered in 1950. Yukawa won the Nobel Prize in physics in 1949; Powell got it in 1950. The discovery of the pion was only part of an avalanche of discoveries of particles in the postwar period -- particles appearing in such proliferation that they reduced the physics community to confusion. As it turned out, physicists ended up "inventing" a great number of particles, and it got to the point where they didn't enjoy it any more.
BACK_TO_TOP* As mentioned earlier, Paul Dirac had discovered the positron in the late 1920s -- while he was conducting studies to describe the electromagnetic field in a quantum context, with "virtual" photons acting as the carrier of an exchange force binding together or repelling electrically charged particles. However, progress on a satisfactory theory proved slow, theories being plagued by unresolvable infinities, caused by the electromagnetic interaction of the electron with itself. With the coming of World War II, physicists had other things to worry about for a while, and there was also a sense of frustration that it was all a dead end.
The breakthrough took place in 1947, when the American physicist Willis Lamb (1913:2008) and his colleague Robert Retherford (1912:1981) performed studies of the energy states of the hydrogen atom, showing there was a previously unknown "splitting" of energy states, meaning that where there had been thought to be one energy state there was actually two. The difference between these two states became known as the "Lamb shift". Lamb would share the 1955 Nobel Prize in physics with the German-born American physicist Polykarp Kusch (1911:1993), who had performed similar studies in parallel with Lamb. A British researcher had actually discovered the shift earlier, but his professor convinced him that he had made a mistake.
The discovery of the Lamb shift provided a clue to the interactions of light and electrons; as theory stood at the time, there was no provision for it, and simply fitting into the theory showed that the Lamb shift should be infinite. That might have seemed like more frustration, but in fact the value of the Lamb shift opened the door, suggesting that trickery invoked to give the proper value might just get things on the right track. Another contemporary discovery, a much-improved measurement of the magnetic moment of the electron performed in 1948, also provided a useful constraint.
The theoreticians eliminated the infinities through a process called "renormalization" in which one infinity was nulled out by another to give a specific value. Since that's a mathematically ambiguous operation, the equations had to then be constrained by the values of known results to get them to work. It was an ugly approach, but it did have the virtue of getting things to work.
There was still the problem that though the results of the system of equations used were consistent with relativity, each of the individual terms was not, which was regarded as unsatisfactory. In the early 1950s, the Japanese physicist Tomonaga Shinichiro (1906:1979), a university classmate of Yukawa Hideki, and the American physicists Julian Schwinger (1918:1994) and Richard Feynman managed to independently come up with a system of equations that were individually consistent with relativity.
The result became known as "quantum electrodynamics (QED)", and Tomonaga, Schwinger, and Feynman shared the 1965 Nobel Prize in physics for it. They had to wait so long because Niels Bohr, who was on the Nobel Committee, didn't like QED, and it wasn't until after his death in 1962 that QED made it onto the list for consideration. When the prize was announced, Robert Oppenheimer sent Feynman a telegram that simply said: "ENFIN" -- French for "at last".
Tomonaga and Schwinger took a strictly mathematical approach in their studies of QED, while Feynman took a more easily understood graphical approach. Feynman described the paths of particles through spacetime with what became appropriately known as "Feynman diagrams". Feynman's approach proved the most popular, possibly partly because he was an outstanding lecturer and could sell his ideas much more easily than most other physicists. Later in the 1950s the British-born American physicist Freeman Dyson (1923:2020) would show, not too surprisingly, that the Feynman diagrams could be derived from Tomonaga's and Schwinger's equations.
Of course, even with Feynman diagrams, QED is fairly tough going. After Feynman won the Nobel Prize, a TV reporter had the bad judgement to ask him to describe the matter in 20 seconds for the viewing audience. Feynman shot back: "If I could describe it in 20 seconds, I wouldn't have won the Nobel Prize."
* The electromagnetic field is an interaction of electrically charged particles, with the photon acting as the force carrier. The essence of QED is the interaction of photons and electrons, since once that is understood, the interaction of photons and other charged particles amounts to variations on the same theme. Dick Feynman pointed out that the interaction of photons and electrons could be understood in terms of three probabilities:
If these probabilities are known, then the interaction of a photon and an electron can be understood. More complicated systems can be understood, at least statistically, as made up of a set of individual interactions.
This all seems fairly straightforward, at least to someone with some familiarity with quantum physics, but to no surprise to someone with such a background, it gets much more devious. Figuring out the probability of a photon going from point A to point B might seem to start with imagining that the photon travels in a straight line between the two points, but Feynman said that what it really involved was figuring the sum of probabilities of the photon going from point A to point B by every possible path, even ones that are ridiculously roundabout and convoluted. This was an application of what quantum physicists now call the "totalitarian theorem": whatever is not forbidden is compulsory, or in other terms, anything that can possibly happen, will happen -- at its appropriate level of probability.
Somebody who knew Feynman suggested that Feynman came up with the idea by simply asking himself: "If I were an electron, what would I do?" Feynman later filled in the answer, which gave an answer that would have almost been obvious to anyone who knew him: "The electron does anything it likes. It just goes in any direction at any speed, forward or backward in time, and then you add up all the amplitudes, and it gives you [the answer]."
This is called the "path integral" or "sum over histories" approach -- the word "history" in this context meaning any of the possible paths of the photon. The approach was not without precedent, since centuries before the great Dutch physicist Christiaan Huygens (1629:1695) had explained light interference effects by summing up the interactions of an infinite number of points making up a set of light-emitting sources.
In more modern terms, it makes a certain sort of sense to anyone who understands the paradox inherent in the two-slit interference experiment, which one of the reasons Feynman said that all paradoxes in quantum physics "were like that". If a single photon is fired at the two slits, then the end result, the interference pattern, has to be understood in terms of two possible paths, one through each slit. Go to four slits, there are four possible paths; go to eight, there's eight; until in the limit of no obstruction whatsoever there's an infinity of possible paths. In the sum, however, the probabilities add up so that the photon appears to go from point A to point B by a straight line.
This concept of sum over histories provides an alternative to the Schroedinger equation and the Copenhagen interpretation, and in fact the sum over histories approach has advocates who insist that it is a much easier way to do things. Instead of a photon or electron or other quantum entity represented as a probabilistic wavefunction and not existing until it is measured, sum over histories says that it exists over all possible paths and the measured value is simply a sum of all those paths.
* Feynman's sum over histories seems at first glance a ridiculous complication that ought to be carved away by Occam's Razor -- the principle that logical excess baggage should be discarded -- but it's just a model that accounts for observations, an accounting trick if one likes, and all are welcome a more convenient accounting tricks, if any can be found. As Feynman pointed out that the QED approach gives results that are consistent with experiment, and that's the bottom line in the sciences.
Suppose Alice, our physics student, looks at her reflection of a point light source in a mirror, with a barrier in the line of sight between her and the light source. By classical physics, the reflected light will arrive by a single path, with the angle of incidence equal to the angle of reflection. By QED, however, the light is reflected from every point on the glass, with the angles being any required to allow the light to reach her eye. The sum of probabilities of these reflections ends up giving the same result as classical physics, with the most probable path being the single path with the same angle of incidence and reflection. This is the "least time" path, the path that takes the least possible time of all those available.
That doesn't seem to buy anything either -- but now suppose a set of opaque stripes is laid down across the mirror. What that does is eliminate some of the canceling paths, so the light will be seen coming from parts of the mirror where it could not be seen when the stripes weren't present. The cancellation pattern will be different for different wavelengths of light, effectively separating the colors of a white-light source into a rainbow of its components. This describes a diffraction grating.
This analysis assumes that light travels in straight lines from the light source to the mirror, and then in straight lines from the mirror to the eye. Actually, as stated before, it takes every crazy possible path available. The end result of the path integral ends up being the same.
* Of course, the interaction between photons and electrons is closer to the heart of QED. Dirac's original work in 1929 described the interactions between an electron and a photon, but he couldn't get the results to agree very well with experiment. In 1948, Schwinger realized that the problem was that the electron could also emit and re-absorb a photon while it was interacting with another photon. That was only one of the possible variations on the theme, and to get the right results meant determining them all and adding up the probabilities. After painstaking effort, the results finally began to converge with experimental reality. Modern results give agreement with experimental results down to ten decimal places. This is about equivalent to determining the accuracy of the distance from New York to Los Angeles to a width of a hair.
Not at all incidentally, the possible variations on the theme can get extremely baroque. For example, a high-energy gamma-ray photon can spontaneously be converted into an electron and a positron -- pair production. Feynman came up with a description of this process that is conceptually elegant, if on the bizarre side. He showed that the pair production caused by the gamma-ray photon was equivalent to a collision between the photon and an electron that sends the electron flying backwards in time, which reverses its charge by a certain "double negative" or "taking away negative charge" logic, turning it into a positron; this reversal is referred to as "charge conjugation". The positron moving backward in time then encounters a gamma-ray photon that causes it to recoil forward in time, turning it back into an electron.
The exact same scenario also applied to electron-positron annihilation, just with the time sense reversed. It also applied to electron scattering by a gamma-ray photon, just with the diagram rotated -- incidentally, since photons have neither charge nor time sense, moving at the speed of light, as far as a Feynman diagram goes they can be regarded as moving in either time direction.
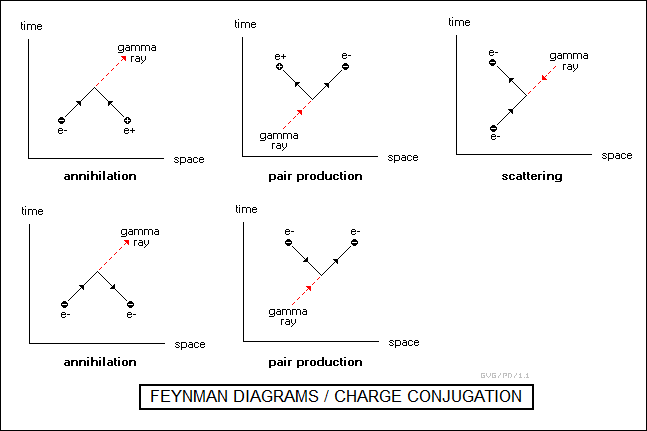
The variations on the theme that caused all the trouble with developing QED involved the production and absorption of photons by a single electron, with the photons possibly turning into an electron-positron pair and then back into a photon, and so on. This is where the infinities arose that plagued the theory. The discovery of the Lamb shift helped drive a solution.
The solution relied on what is known as "perturbation theory", which is more a calculational algorithm than a theory as such, a type of successive approximation method. The self-interaction of the electron could be approximated by assuming the simplest possible and most probable interaction, the emission and re-absorption of a single photon by an electron. This would yield an answer, which could then be adjusted by considering the second simplest and probable interaction, the emission of two photons, and adding in that result.
Further, if increasingly smaller, adjustments could be made by considering successively more complicated interactions -- with the probability of such interactions decreasing rapidly as their complexity increased -- until the result of the "perturbation series" no longer changed at the desired level of decimal places. By the end of the 20th century, the perturbation series had been worked out to the eighth level of interactions, which gave a total of almost a thousand distinct interactions.
Renormalization, the nulling of infinities by infinities, was needed to calculate the terms. Unfortunately, renormalization was the sort of approach that might work, might not, and the only reason it could be said to work was because the results agreed with experiment. Mathematicians hated it; Feynman called renormalization "dippy" and believed, as most physicists still do, that QED will be revised in the future to get rid of it. Although Dirac was the intellectual grandfather of QED, he was too much of a purist to ever like renormalization, and was very suspicious of QED as it emerged in the 1950s.
Incidentally, the fact that an electron is surrounded at all times by a cloud of virtual particles means that the charge of the electron that is observed by experiment is not the same as the charge of the electron all by itself. This charge, known as the "bare charge", is the one that must be used in Feynman diagrams, while the actual observed charge is known as the "dressed charge". The same concept applies to the electron mass: it has a "bare mass" that is not quite the same as its "dressed mass".
BACK_TO_TOP* As something of a footnote to QED, Feynman's development of the theory showed why he was one of the most intriguing figures in science. He came up with the notion of particles moving backwards and forwards in time when he was a graduate student at Princeton, working under John A. Wheeler. Wheeler liked to assign his students difficult problems and then let them go at them, handing out the occasional hint or suggestion as seemed useful.
In 1940, Feynman was tinkering with the electrodynamics of the solitary electron and trying to figure out how to get rid of the ugly infinities, nobody having thought of renormalization just yet. At first, he thought he might overcome the problem by simply assuming an electron didn't interact with itself, but that was a non-starter. A charged particle, even one in relative isolation, has a certain resistance to motion above its ordinary inertia, and it was troublesome to figure out how this "radiation resistance" could arise if an electron didn't have self-interactions.
Then Feynman switched to the opposite approach, assuming there really wasn't any such thing as an isolated electron. Would electromagnetism actually exist if there was only a single charged particle in the entire Universe? Feynman postulated that there needed to be other charged particles, with exchanges of photons between them creating the electromagnetic force. The problem was this was that radiation resistance was an immediate sort of thing -- push an electron and the resistance is there, with no delay of any sort. If it had something to do with exchanges of photons, and if the only charged particles were a distance away, it would seem that the effects would be delayed by the time it took photons to shuttle back and forth.
Feynman got a leg up on his next step from Wheeler, and it was a big step indeed. It was known that at the level of fundamental interactions, physics doesn't generally make any distinction about the direction of time. A video of a collision between two particles makes sense whether it's run forward or backwards. Of course, for systems of particles it's easy to see the direction of time, which is in the direction of increasing thermal disorder or "entropy".
Maxwell's equations, which defined the action of electromagnetism, are time-symmetric, meaning that a video made of the interactions defined by those equations worked as well in forward as in reverse, though it required reversing electric charge -- leading to the concept of charge conjugation discussed in the previous section. One day Wheeler bounced a wild idea off of Feynman, saying: "I know why all the electrons have the same charge and same mass."
"Why?"
"Because they're all the same electron." The idea was that there was only a single electron in all the Universe, bouncing back and forth through time. It was an interesting notion, but the problem was that it implied an equal number of electrons and positrons in our Universe, which didn't seem to be the case even at the time, and which nobody seriously believes now.
In addition, the avenue that Feynman was moving down had been established by Dirac with one goal of consistency with Einstein's theory of relativity. According to relativity, time slows down for an object as it approaches the speed of light. Since light itself of course moves at the speed of light, time doesn't exist for light. From the point of view of a photon, any consideration of time was irrelevant, and so any consideration of the direction of time was irrelevant as well.
Feynman was now able to describe the radiation resistance of an electron as due to interactions with other charged particles, no matter how distant, by assuming an electron emitted photons both forward and backward in time. The photons moving forward in time are known as "retarded waves", since there is a delay between the emission and reception, while the photons moving backward in time are similarly known as "advanced waves".
In early 1941, Feynman gave a lecture on the "Wheeler-Feynman absorber theory", as it was named, to the physics department of Princeton. At the time, Princeton's physics faculty included Pauli and Einstein. Pauli expressed mild, by his standards, skepticism about the notion, but Einstein was intrigued: "No, the theory seems possible." It was grand praise for a graduate student. Feynman's doctoral thesis of 1942 was built around the concept; he then went off to Los Alamos to work on the atomic bomb project, and the evolution of absorber theory into QED would have to wait until the war was over.
* QED might sound muddled and mystical, and in fact when Feynman first told Freeman Dyson about the sum-over-histories notion, Dyson replied: "You're nuts." Feynman himself called it "the strange theory of light and matter." It is "strange", and anybody doing ordinary practical work in optics, electromagnetics, or chemistry has little or no use for it. However, it is the "theory of light and matter" that provides a solid theoretical foundation for such work, as well as almost every other phenomena observed in the macroscale except those involving gravity. Such is the power of its methods that it is regarded as one of the "crown jewels" of theoretical physics.
Feynman had an outgoing, energetic personality and an extravagant sense of humor; he became well-known to the public through a set of books that described his personal adventures and misadventures, such as his hobby of safecracking when he was at Los Alamos during the war. The stories were clearly egocentric, and in some cases seem to have had a tenuous relationship to reality. Some regarded Feynman as flamboyant, fun-loving, and direct, while others found him show-offy, volatile, confrontational, abrasive, and obnoxious. Some of his students were downright terrified of him. Almost everyone admitted he was brilliant: "Like Dirac, only human" -- was how Eugene Wigner, Dirac's brother-in-law, described Feynman.
Freeman Dyson saw both sides of Feynman at the very start, his initial impression of Feynman being that he was "half genius and half buffoon". Feynman later bought a 1975 Dodge van and had Feynman diagrams painted on it for all to see. When asked why he had done so, he answered: "Because I'm Dick Feynman."
Although Feynman and Julian Schwinger had a lot in common -- both Jewish, both from the New York City metro area, both the same age -- and fought out their ideas on QED against each other, there was a certain comical clash of styles between the two. Physicists, particularly those at the genius level, are not necessarily anything that could pass for "ordinary folks" and may have difficulties being accepted as such by their neighbors. If so, they have a choice of either charging forward regardless or keeping a low profile. Feynman charged. He was extroverted in the extreme, cocky, outspoken, casual, and gregarious. Schwinger kept a low profile. He was shy, quiet, cool, aloof, was almost always dressed in expensive tailored suits, and drove an immaculate Cadillac.
Schwinger usually rose at noon and worked nights to ensure his privacy, and as a mathematical prodigy from a young age -- one who knew him called him a "Mozart of mathematics", as a high-schooler reading papers by Dirac -- he loved mathematical complexity for its own sake. Schwinger was inclined to make up his own mathematical notations, as if trying to make it harder for people to understand him -- it became known as "Schwingerese", and was a bit of a handicap for his students when they had to deal with the rest of the world -- and he actually disliked Feynman diagrams because they were easier to understand, preferring his own more strictly mathematical approach. In practice, physicists prefer to use Feynmann diagrams for teaching and for investigating ideas, while using Schwinger's equations when "heavy lifting" is required.
Incidentally, although Freeman Dyson never reached a level of influence in his field close to that of the towering Dick Feynman, Dyson wrote a set of highly readable and sparkling popular books, full of brilliantly imaginative speculations, that gave him a comparable level of visibility with the public. Dyson himself commented on the irony that he will almost certainly be much more remembered for his speculative concepts -- such as the "Dyson sphere", in which an advanced civilization dismantles a planet to build a shell around a sun to provide more living space -- than his professional work.
Unfortunately, in his declining years, Dyson became a prominent climate-change denier, attempting to undermine climate research with dubious and dishonest criticisms, which did much to undermine his reputation. Physicists have an unfortunate inclination to believe in the superiority of their field of science to others -- which on occasion leads to getting in over their heads in domains where they have no credible expertise.
BACK_TO_TOP* One of the implications of QED is that what we think of as empty space isn't really empty at all. Pairs of virtual particles and antiparticles are being created and destroyed all the time, popping in and out of existence so fast that they can't be detected, at least not directly. One of the implications is that there is an energy, known as "zero point energy (ZPE)", inherent in the vacuum itself.
The zero point energy can be detected indirectly, if just barely. The Lamb shift that led to the development of modern QED is due to the ZPE, as is the unavoidable "quantum noise" that becomes a fundamental barrier to sensitivity in electronic and optical equipment. The best known of the phenomena that illustrate the existence of zero point energy is the "Casimir effect", discovered in 1948 by Dutch physicist Hendrik B.G. Casimir (1909:2000).
If two metal plates are set up in a vacuum, they will act as a resonant chamber for virtual photons, and this will result in a faint but measurable net force on the plates. The reason is that in the region between the plates, the electromagnetic waves manifested by the zero point energy cannot have wavelengths longer than the spacing between the plates. This constrains the possible wavelengths of the trapped electromagnetic waves, while electromagnetic waves outside of the two panels are not constrained.
The imbalance results in a very tiny force. Measurements have been conducted using a "torsion pendulum" mounted in a vacuum chamber, with the force exerted between two plate moving the pendulum. The motion was so slight that it had to be measured by using a precision laser system; it was about equivalent to the gravitational force exerted by the entire Earth on an amoeba.
There is a faction of ZPE enthusiasts, including a cadre of science-fiction fans, that still believe there are enormous energies available from the vacuum. In any volume of space, the ZPE could support electromagnetic waves with an infinite number of frequencies, and so could conceivably provide access to an infinite amount of energy. Skeptics believe the infinities are mathematical artifacts that will eventually be eliminated. The presence of infinite amounts of energy built into space itself implies, through Einstein's E=M*C^2 mass-energy relation, a mass of the Universe far greater than that which is implied by observations of the expansion of the Universe, and correspondingly requires a number of awkward assumptions to make observations fit with theory. One critic of the ZPE advocates has countered mildly: "One has to keep an open mind, but the concepts I've seen so far would violate energy conservation."
The uncertainty principle says that the greater the energy of a virtual particle, the shorter the time it exists, and it is hard to figure out any way of getting around this obstacle. However, some physicists have speculated that under the right circumstances a virtual event might propagate into an entire Universe of its own, as long as the energies balanced out. Given the Heisenberg uncertainty relation:
delta_energy * delta_time = hbar
-- then if the net energy or "delta_energy" of the new Universe is close to zero, the lifetime or "delta_time" could be very long. The idea of the spontaneous creation of the Universe from a fluctuation of the vacuum was apparently first suggested in a 1973 paper by Edward Tryon of the City University of New York, in which he dryly concluded: "I offer the modest proposal that our Universe is simply one of those things which happens from time to time." He later added: "This proposal struck people as preposterous, enchanting, or both."
This notion has since been expanded into a vision, most prominently associated with the Russian-American physicist Andrei Linde (born 1948) but not unique to him, of branching trees of universes giving rise to new universes, possibly with different laws of physics, performing an evolution in which some universes survive and others are stillborn. In this view, while our own Universe clearly had a beginning and will eventually have an end, the branching tree of the "multiverse" may have had no beginning and may not have an end.
It might be even possible to force the generation of a new universe, and so it is conceivable that a physicist might be able to play God in an uncomfortably strong sense. Even the most outspoken atheist might have hesitations about such a course of action, but that issue can be sidestepped for now, since nobody expects to have the capability of performing an experiment along such lines any time soon.
BACK_TO_TOP* ZPE is a startling idea, and there are doubts it amounts to anything. Modern quantum physics has ideas in play that are at least as startling, and they do amount to something.
The two-slit interference experiment shows that quantum entities like photons or electrons don't actually exist in a well-defined state until they are observed. Until they are observed, they exist simultaneously in the range of all their possible states, or in a "superposition of states". Once they are observed, the observation causes a "collapse of the wavefunction" or "decoherence". Superposition of states was discussed earlier in this document and then ignored, partly because it was hard to see what to make of it. However, it does have practical, or at least potentially practical, applications in the field of "quantum computing".
A normal computer processor essentially performs operations on a single number at a time. A scheme can be imagined with quantum physics that can perform operations on a full range of numbers at a time. In 1985 In that year, following up on hints provided by Feynman, a British physicist named David Deutsch (born 1953) of the University of Oxford published a paper that suggested that superposition of states could be put to use in a "quantum computer".
A conventional computer encodes a bit, a 1 or 0, as the presence or absence of a voltage. A quantum computer, in contrast, uses a quantum-mechanical property of a particle to encode a 1 or 0, for example the spin value or the polarization of a photon. In either case, calculations will be performed on a group of bits, say 32 bits, at one time. 32 bits can be arranged in a total of 4,294,967,296 different ways, allowing them to encode that number of different numbers. Suppose a conventional computer were to perform a calculation requiring a test of all possible values that can be represented by 32 bits. It would have to loop through every single value, one at a time.
In contrast, if a 32-bit value was represented by the spin states of 32 electrons or the polarization states of 32 photons, by the principle of superposition of states, all possible 32-bit values would be present at the same time! A quantum computer operating on these 32 particles could test all 4,294,967,296 values in a single calculation, without going in a loop. While adding another bit doubles the number of loops for a conventional computer, even if another bit is added to the calculation in a quantum computer, the calculation would still be done at one time and would take no longer than before. The hardware would have to get bigger, but the computation time would remain the same.
Since the use of the spin state of an electron or polarization state of a photon to represent a bit has vastly different properties from the use of a voltage level to represent a bit, in a quantum computer the bits are referred to as "quantum bits" or "qubits". Deutsch's idea was purely abstract idea at the time, but there have been proof-of-concept lab demonstrations, and even some limited-function quantum computing machines.
* Along with quantum computing, there's also work on cryptological schemes based on another strange aspect of quantum physics, known as "entanglement" -- rooted in the "EPR paradox" and "quantum nonlocality".
As mentioned earlier, although Einstein eventually agreed that quantum physics was correct, he continued to insist that it wasn't complete, that there was something left out. In 1935 he published a paper co-authored by his assistant, Nathan Rosen (1909:1995), and another physicist, Boris Podolsky (1896:1966). The paper became known as the "EPR paper" after "Einstein-Podolsky-Rosen". The EPR paper imagined the simultaneous generation of two particles that had interlinked properties -- for example, two electrons with opposed spins, or two photons with polarizations at right angles to each other. Entangled photons with a right-angle polarization relationship can be generated, for example, by electron-positron annihilation, which produces gamma-ray photons; or, more practically, by shining a laser beam through certain types of optically-active crystals.
The two particles propagate in opposite directions. Their state is unknown until one is measured, to obtain its spin or polarization as the case may be -- but then the state of the other one is known, no matter how far away it is. Erwin Schroedinger described the photons as "entangled". This "EPR paradox" seemed to violate Einstein's theory of relativity, which stated that nothing can travel faster than the speed of light, or in other words implied "quantum nonlocality". He referred to this notion as "spooky action at a distance."
Einstein said the EPR paradox showed that the photons were not actually undefined before they were measured, with their state specified by "hidden variables". Pauli and Heisenberg were outraged; Niels Bohr was all but in shock, but he rallied to give a refutation of the EPR paper, commenting:
QUOTE:
... the observer and the [entangled particles] are part of a single system. And that system doesn't care about our ideas of what's local and what's not. Once connected, atomic systems never disentangle at all, no matter how far apart they are ... sad to say, [EPR] is not even a paradox!
END_QUOTE
That was a fuzzy sort of answer -- but then, it was a fuzzy sort of question. At the time, the argument was basically philosophical, something of a matter of opinion, a science-fiction notion that couldn't be tested, and that was essentially all it was for three decades.
In 1951 David Bohm (1917:1992), a Left-leaning American physicist who had gone to work in Britain because of the Red Scare hysteria back in the US, published a refined version of the EPR paradox, but his work had little impact at the time. Then, beginning in the 1970s, devious experiments showed that the quantum nonlocality was the way things actually worked.
* Quantum nonlocality would seem to suggest schemes of faster-than-light communications, but no. Suppose Alice & Bob are each given a box, one with a gold coin, the other with a silver, and take off in starships in opposite directions. Some time later, Alice opens her box, and finds she has a gold coin; she then knows that Bob has the silver coin. Bob similarly opens his box, to find he has the gold coin, and so Alice has the silver coin. It matters not at all which of the two opens their box first. There is no communication of any information between Alice and Bob in this case, and Alice cannot inform Bob of her discovery except by conventional communications channels.
This scenario is not quite the same as the EPR paradox, which adds the, shall we say, fascinating aspect that the contents of the boxes are undefined -- a half probability of a gold coin, a half probability of a silver coin -- until Alice opens her box. Of course, while this is a useless scheme for faster-than-light communications, it works out very well, at least in principle, for cryptography.
Suppose Alice and Bob both have "tanks" of entangled photons. Alice can then measure the polarizations of photons in her tank, reporting to Bob over a clear channel which one of the set she measured and how she measured it. Bob can then measure the polarizations of his own photons. The orientation of the polarizations of the photons can then be used to determine a mutually-agreed cipher key without trading any information that could be intercepted by an eavesdropper. Any attempt to intercept Bob's photon would accomplish nothing but to disrupt the transaction.
* Incidentally, although using quantum nonlocality for cryptography is a fairly obscure subject, the phenomenon has picked up a lot of publicity because it also implies what is called, somewhat confusingly, "quantum teleportation". It works as follows:
It should be noted that this only transfers the state of Alice's electron as it was at the time of the interaction; the interaction changes its state. It is as though it were "teleported" from Alice to Bob, hence the name of the process.
It should also be noted that this scheme also doesn't imply faster than light communications. Bob cannot check periodically on his photon without disturbing its state and destroying the entanglement, so he has to be tipped off by Alice after she does her own measurement, and he cannot figure out the state of his electron without knowing the results of Alice's experiment. Alice cannot communicate this information to him faster than the speed of light. Even if she could, quantum teleportation only really works for simple quantum entities, and it is hard to see how it could be scaled up to more complicated things. As some of those working in the field have suggested: "It's teleportation, Jim, but not as we know it."
* As a footnote -- discussions of quantum superposition, nonlocality, and teleportation point to the difficulties of trying to come to grips with what's going in the quantum world. Under the Copenhagen interpretation, the answer is simple:
There has long been a faction in the physics community that needs more. As mentioned, Louis de Broglie had suggested in 1927 that the Schroedinger wavefunction was not just a probability distribution; it was a real function that guided real particles along their paths. The Copenhagen clique rejected this notion, denying the notion of hidden variables that it implied and judging the whole idea just so much excess baggage. De Broglie also had problems working out the math and getting the concept to work.
However, the idea didn't go away, though it went underground for a long time. In 1952, David Bohm published two papers that revived and extended de Broglie's original concepts. Bohm's concepts envisioned that the Schroedinger wavefunction included a form of energy not known to classical physics that was related to what he called the "quantum potential" or "pilot wave". In the two-slit experiment, the pilot wave would exist through both slits and guide real particles through the slits to obtain an interference pattern. Although the de Broglie-Bohm interpretation does state that there is a real particle following a real path, the statistical nature of the wavefunction and the Heisenberg uncertainty principle remain in effect: only probabilities for the location of particles can be determined. Similarly, the de Broglie-Bohm view retains decoherence: attempting to observe the interaction would interfere with the pilot wave and eliminate the interference pattern, as is observed.
There was the troublesome issue of fitting quantum nonlocality into the theory, but Bohm proposed that there was a special "preferred" frame of reference where the instantaneous action occurred. This was such a clunky idea that it was no surprise many physicists rejected it. In the end, the existence of quantum nonlocality was demonstrably proven -- but the question still remained of whether it made any more sense under the de Broglie-Bohm theory than it did otherwise. Indeed, what did the de Broglie-Bohm theory bring to the party? It left physicists no wiser.
The same can be said of the "quantum multiverse" or "many-worlds" theory, which has obtained a certain notoriety, often being seen in science-fiction stories. The basic idea was developed in 1957 by Hugh Everett III (1930:1982), then at Princeton. The basic idea is that an observation of a quantum system that has a range of possible values actually results in the manifestation of all possible states, but with each result in its own branching parallel universe. In other words, at all times an infinity of parallel universes are being born from our universe.
In the many-worlds scheme, Schroedinger's cat is not half-alive and half-dead. It is alive in one universe and dead in another, and the act of observation places us in one of these two particular universes. In the two-slit interference experiment, a photon will go through one slit in one universe and the other in a second universe. In interfering, the photon will merge the two universes.
The central difficulty with the many-worlds scheme is that we can only say something exists if it can be reliably observed. By the definition of the scheme, we can only observe one Universe, with all the others being no more than fictions. Anything in a theory of science that isn't connected to observations is a convenient accounting rule at best, useless excess baggage at worst. It would be less cumbersome to simply speak in abstract of "many histories", as in Feynman's sum-over-histories approach to QED, and nobody could show that there was anything much changed or lost thereby.
Another approach, known as "quantum logic" and promoted by von Neumann, attempts to take the rules of quantum physics, simply accept them as givens, and construct a logical system of rules out of them. This has a certain appeal at first sight -- but as one physicist put it, it was like "inventing a new logic to maintain the Earth is flat if confronted with the evidence that it is round."
It is hard to see that quantum logic could really buy us any further understanding of the Universe. It is just a reshuffling of what we already know, and ends up being excess baggage as well. Again, once we reach the limit of observations, it is futile to ask WHY something is the way it is. Why does an electron have the properties it does? Since it can't be broken down into smaller particles, the only answer is that if it didn't have those properties, it would be something else.
BACK_TO_TOP