
* We're all familiar with the matter that makes up the world and ourselves, as well as the fact that it comes in three different forms: as solid, liquid, or gas. This chapter discusses the properties of solid matter, with a focus on the applications of those principles to the design of structures. Liquids and gases are discussed in the next chapter.
* The idea that matter could be broken down into submicroscopic individual units, known as "atoms", goes back to antiquity, though the concept didn't start to acquire scientific momentum until 1808, when the English scientist John Dalton (1766:1844) proposed it to account for the results of his studies of chemical reactions. Today, it is known that there are about a hundred different types of atoms with different weights and other properties. These "elements" include hydrogen, the lightest and most common element; carbon, which makes up soot; silicon, one of the constituents of sand; metals like gold, iron, and lead; the gaseous elements oxygen and nitrogen; and many others.
Atoms could also be combined to form "molecules". For example, if the element oxygen is burned with the element hydrogen, each oxygen atom forms "chemical bonds" with two hydrogen atoms to form water molecules. It was the distinct and predictable patterns of combinations of atoms into molecules that led Dalton to propose the atomic theory. Large numbers of atoms can combine into a single molecule, particularly in the case of the complex carbon-based "biomolecules" that make up living organisms, and the materials made from atoms and molecules can be arranged into large-scale systems, from stones to machines to flowers to human beings.
Detailed discussion of chemical reactions, in which atoms are converted into molecules or molecules are broken down into atoms, is discussed in a companion document on chemistry. However, it is useful to comment here that such chemical reactions observe the fundamental law of energy conservation as obeyed in physics in general. Reactions may be "exothermic", releasing energy stored in chemical bonds, or "endothermic", absorbing energy stored into chemical bonds; but in any case the total energy before and after the reaction will remain the same. Only the forms are changed.
For example, water can be broken down into hydrogen and oxygen by running an electric current through it; this is an endothermic process. A spark will then cause the hydrogen and oxygen to explosively recombine; this is an exothermic process. On a broader canvas, a tree grows by using sunlight and raw materials such as water and carbon dioxide to drive its complicated biological processes, which in sum amounts to an endothermic process. The wood can be burned to release its energy, which is an exothermic process.
* Oddly, although atomic theory now seems to be an essential element of classical physics, it wasn't completely accepted by physicists until the early 1900s. Ironically, this was at the very time that the doctrines of classical physics would begin to be seriously challenged.
Atoms had been originally thought of as indivisible, but even before the final triumph of atomic theory physicists were beginning to realize that atoms themselves were not indivisible and had an internal structure. They gradually realized that an atom had a heavy central "nucleus" that had positive electric charge, surrounded by light orbiting "electrons" that had a negative electric charge. Electrons could be stripped from atoms to be sent through wires as electrical currents. If an atom lost its normal complement of electrons, it became a positively charged "ion". Atoms could also acquire an excess of electrons, becoming negatively charged ions. Such charge imbalances were one mechanism that contributed to the bonding of atoms into molecules, though subtler processes were involved as well.
Physicists soon found that the interior of the atom was a complicated place where things happened that were impossible at a larger scale, and this simple model of a "classical atom" had to be revised. The revisions lead into the realm of modern physics and so are beyond the scope of this document. The classical atom still provides a useful basis for the discussion of the fundamental properties of matter.
BACK_TO_TOP* Solid matter covers a wide range of forms, everything from a compacted block of trash containing every form of household rubbish to a glittering diamond, consisting of carbon atoms arranged in an orderly, uniform "crystalline" arrangement.
At a high level of abstraction, chunks of matter have certain properties that can be characterized and measured, for example color; density, or ratio of mass to volume; and various measures of strength, or the ability of that chunk of matter to retain its structure or "integrity" when subjected to various forces. Obviously these things are much easier to characterize with, say, a diamond than for a block of compacted trash.
Solid matter also has certain properties of "scale" that are independent of what the matter is made up of. For example, let's take a set of cubes of solid matter without regard to what the matter is. Suppose one cube is a centimeter on a side. Now let's suppose Bob stacks up the cubes to make a bigger cube that is two centimeters on a side. This doubles the linear dimensions of the cube. The surface area of the cube has expanded by a factor of four, while the volume and mass of the cube has expanded by a factor of eight; doubling the linear dimensions of an object squares its surface area and cubes its volume and mass. This means that as an object grows bigger, its volume and mass increase much more rapidly than its surface area.
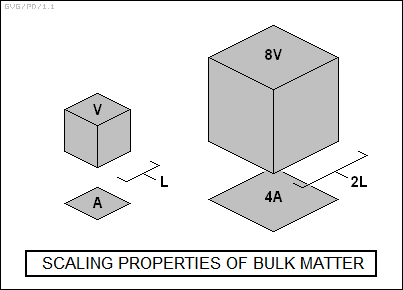
1950s horror movies such as THEM envisioned monster ants, but in fact such scaling effects prevent insects from becoming very large. For one thing, they don't have lungs, and have to acquire oxygen through pores in their chitinous skins. Doubling their size would increase their volume and mass twice as fast as it would increase their surface area, halving their ability to obtain oxygen for that mass, and at a certain size a giant insect would simply suffocate.
A more important scaling issue that rules out giant insects is the issue of "compressive strength", or the ability of a structural support to bear weight placed on top of it. The compressive strength of a structural support, such as a column that holds up a building, is proportional to the cross-sectional area of a horizontal slice through the column. A cross-section is just one face of the surface of an object, and so like surface area increases with the square of a linear increase in size. However, the mass of the building increases with the cube of a linear increase in size.
Double the linear dimensions of a building and the ability of a column to support the building's weight is increased by four, while the mass and the load on the column is increased by eight. The column now has to proportionately bear twice as much load as it did at the smaller scale. This means that more, or disproportionately large, columns must be used to support a larger building. Insects generally have spindly bodies and legs, while an elephant has great stumpy massive legs. If an insect were scaled up to large size, it would simply collapse of its own weight. However, horror movie fans can still take comfort that ghastly venomous or parasitic insects are not ruled out by the laws of physics.
BACK_TO_TOP* These considerations of scale lead back to the notion of strength of materials, which in turn leads to consideration of how materials are used for building structures.
Although builders always had useful concepts of what could or could not be done when building structures, the first person to try to perform scientific experiments to determine the strength of materials was the Italian polymath Leonardo da Vinci (1452:1519). The first formal text on the subject of materials was actually published late in life by Galileo in 1638, titled DIALOGUES CONCERNING TWO NEW SCIENCES. He was under house arrest at the time, having antagonized the Vatican by promoting the notion that the Earth went around the Sun and not the reverse, and materials seemed like a noncontroversial subject not likely to get him into further trouble.
Galileo's DIALOGUES were not particularly correct in all details -- the basic laws of physics required hadn't been invented just yet -- but the book did get people thinking. Isaac Newton had little interest in the subject of materials, but his rival Robert Hooke was fascinated by the subject, examining the ways in which materials responded to forces, in particular coming up with Hooke's law. This was mentioned in a previous chapter as:
force = stiffness * compression
It was stated then as applying to a spring, but it also applies to structural elements made of hard metals, stone, and glass. It does not in general apply to flexible materials like rubber or tendon, which stretch easily up to a limit but then yield diminishing returns.
Hooke's work was the first to at least imply the notions of "stress" and "strain". Stress is a force applied to a structural element. Such forces include:
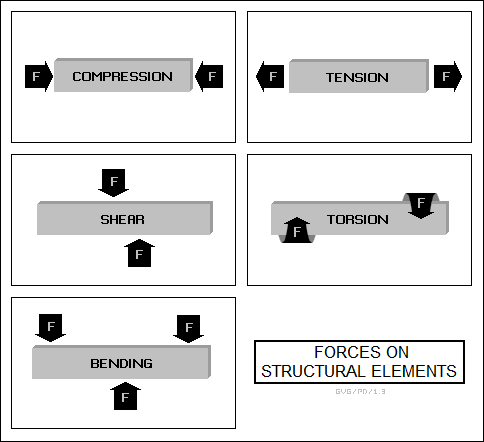
Stress is measured in terms of force per unit of area, or what is simply known as "pressure". The formal metric unit of pressure is the "pascal (pa)", which is a newton per square meter, named after the great French mathematician and physicist Blaise Pascal (1623:1662). Since a pascal is a somewhat small unit, it is often expressed in terms of "kilopascals (kpa)" -- thousands of pascals -- or "megapascals (Mpa)" -- millions of pascals.
In compression and tension forces, the force is applied directly through a cross-section of a structural element, and so the stress is measured in terms of Mpa. In shear force, the force is applied along a plane through a structural element, and so stress is measured in terms of Mpa over the area of the interface between the two sections of the structural element.
Torsion is similar to shear, but involves a torque over the area of the interface. Bending is complicated, since it involves a shear force down through the structural element, a tension force along its bottom, and a compression force along its top. In practice, structural elements may be subjected to a number of these stresses at the same time.
A structural element under stress will exhibit a "strain", that is, a lengthening, given in a simple proportion. Up to a certain limit, once the stress is removed, the structural member will return to its original length. This is called "elastic" behavior". It was certainly implied by Hooke, but the idea was developed further by Thomas Young, who published a paper in 1807 in which he defined the concept of "elastic modulus" or "Young's modulus". In modern terms, this is the ratio of stress of a particular material to its strain:
elastic_modulus = stress / strain
It is somewhat more intuitive to express this as:
strain = stress / elastic_modulus
Since strain is a simple proportion, the units of elastic modulus are still Mpa. For materials that stretch easily, the elastic modulus has a low value; for example, rubber has an elastic modulus of 7. The stiffer the material, the higher the elastic modulus:
wood (spruce) 11,000 Mpa ordinary glass 70,000 Mpa steel 201,000 Mpa diamond 1,200,000 Mpa
Given these definitions of stress and strain, then Hooke's law can be rephrased as follows:
force = stress * strain
Hooke's law also leads to the concept of "strain energy", or the potential energy contained in a strained structural element, which is similar to the equation for energy in a stretched spring:
strain_energy = volume * ( 1/2 ) * stress * strain^2
Once the stress on a structural member exceeds a certain limit, the member will be permanently strained out of shape, and will break if the stress is increased. Not all materials respond to forces in such a nice graded way. They may not deform at all up to the level of force where they snap. Such materials are said to be "brittle". Glass is a good example, since any practical experience shows how difficult it is to bend a glass rod without breaking it.
Materials are said to have a "breaking strength" or "tensile strength", rated in the tension stress that causes them to snap. The concept goes back at least to Galileo, who performed tests in breaking strengths, though he didn't have the theoretical tools needed to describe it well. Typical tensile strengths include:
high strength steel 1,500 Mpa ordinary commercial steel 400 Mpa cast iron ~200 Mpa aluminum alloys ~300 Mpa hemp rope 80 Mpa bone 140 Mpa nylon fiber 1,000 Mpa kevlar fiber 2,700 Mpa
Not all materials respond to different forces in the same way. Although metals are strong in both compression and tension, stone is very strong in compression but is weak in tension. Wood can be split easily by shear forces applied along the line of its grain, but will resist larger shear forces applied at a right angle to its grain.
Forces acting consistently on a structural element over a long period of time may cause a slow deformation, or "creep", that can lead to failure even if the elastic limit is never exceeded. Similarly, a cycle of changing stresses repeated over and over may cause "fatigue" that will eventually lead to the failure of a structural element.
* Although Hooke got the ball rolling, the notions of stress and strain were not articulated in their modern form until 1822, in a document published by a French mathematician named Augustin Cauchy (1789:1857). It would take time for Cauchy's work to sink in, since he wrote in a theoretical style that was more or less foreign to engineers, but now his concepts are regarded as one of the major foundations of structural design.
The underlying idea of all structural design is balance of stresses. If the stresses imposed on a structural element exceed the strength of the element, it will collapse. The stresses are set up by what engineers refer to as "loads". Some of the loads on a structure are obvious: the "dead load" set up by the weight of the structure, and the "live load" set up by the people, furnishings, equipment, and materials contained in the structure. These are known as "static loads" because they don't change, or don't change much, over time.
Others loads are not quite so obvious. There are the "hidden" loads, with stresses set up by the expansion or contraction of structural elements due to changes in temperature, or by unequal settling of the building's foundations. Structures may also be subjected to rapidly changing "dynamic" loads, such as those caused by winds and earthquakes.
Dynamic loads can be particularly treacherous since they are somewhat unpredictable. In one famous example, the designer of the Citicorp skyscraper in New York City received a letter from a student who was curious about the building's stability in winds. The architect replied that the building's design had been analyzed to ensure that it would stand up to storm winds and that it was safe. However, after sending his reply, the architect realized that the analysis had been performed with the assumption that the winds would be perpendicular to the faces of the building -- but what if they weren't? He re-did his analysis to see what would happen if the winds were at an angle, and to his shock found out that a severe windstorm would generate torsion forces that would bring the skyscraper down in the middle of Manhattan. The Citicorp building's steel framework was hastily reinforced.
BACK_TO_TOP* Structures can be divided into two classes: compressive structures, in which the structural elements are stacked on top of each other; and tensile or "suspension" structures, in which the structural elements are suspended from supports.
One of the simplest examples of a compression structure is a brick wall, with the bricks piled on top of each other. One of the simplest examples of a tensile structure is a circus tent, with the canvas "big top" held up by ropes hung from a central pole. Of course, in practice most structures feature both compressive and tensile elements.
The first really big structures were compression structures, since it was difficult to build durable large structures of wood, and stone doesn't lend itself to tensile structures. The major problem with stone compressive structures is that stone is very heavy, or more specifically has a low "strength-to-weight" ratio. This means that the weight of such a structure grows very quickly as it the structure grows bigger, and walls have to be made thicker and thicker at the base so the structure doesn't collapse. This approach ultimately leads to the simplest of all large stone structures, the pyramid, built not only in Egypt but in China and in the Pre-Columbian New World as well.
* Pyramids are an impressive but purely brute-force design. Builders were also learning more sophisticated tricks working with wood, the other classic building material. Wood was used to construct ordinary buildings, such as homes, and structures such as bridges.
The earliest wooden bridges no doubt consisted just of two beams set up across a stream and covered with planks. The major problem with this configuration is that such a bridge is limited in length. It is supported at the ends but not in the middle, and as it gets longer so does the "lever arm" of the half-spans of the bridge, meaning that a person stepping on the middle of the bridge places a proportionately greater stress on it. If the bridge was over the top of a shallow stream, this problem could be addressed by driving pilings in the middle of the stream and fastening the middle of the span to them, but if the stream wasn't shallow or if the bridge was over the top of a deep canyon, such a fix wasn't possible.
There were two possible solutions. The first was the rope "suspension bridge", a tension-based design. Wooden or stone towers could be constructed on both sides of the canyon, with heavy ropes slung across their tops and anchored to the ground. A wooden walkway could then be suspended from the ropes. This type of bridge has been around for millennia, and is thoroughly familiar from B-fiction adventure movies since they are excellent sites for dramatic action scenes. They always seem to be in a frighteningly bad state of repair, and the waters beneath are often full of crocodiles, piranhas, snakes, or other nasty creatures.
For present purposes, a second option is more interesting. Suppose Bob has a wooden bridge and wants to brace up the middle of the span from each end. He can do this by fitting a beam from the bank to the midspan at an angle. This allows the forces directed downward at midspan to be shunted towards the banks. Since this sets up a sideways force on the two support beams that tends to splay them apart from the middle, it is also useful to link them together at the bottom with a third beam, forming a triangular support structure known as a "truss".
The truss is a basic structural form, and is composed of various triangular structural subunits linked together. The triangular shape is very useful as it will stand up to stresses imposed in different directions, and it is also employed in the "cross-bracing" of structures used to keep them from falling over in heavy winds and the like. The truss is of course in as wide use as it ever was; one of the tidiest examples is the metal high-voltage transmission line tower, which is often built as a lightweight structure made up of triangular truss elements.

* The problem with wooden bridges is that they didn't tend to last all that long. Stone is far more durable, but it does not lend itself to construction of trusses. However, the same underlying principle of diverting stresses to the sides could be used on stone bridges as well, by building them with curved structures called "arches". The arch did imply the provision of supports to deal with the sideways loads it set up. That was generally simple with bridges, as they might be built between stony riverbanks or -- if such weren't available -- heavy footings could be constructed on each bank.
That could be a tricky matter for other structures. The Gothic cathedrals of Europe, with their high arched or "vaulted" ceilings, were built with "flying buttresses", structures attached to the outside of the building to provide the necessary lateral support. The "dome" was an extension of the arch, rotated around in a full circle. Like the arch, the dome required lateral support to handle the horizontal stresses. Islamic architecture, which demonstrates a certain fondness for domes, often involves half-domes or "semi-domes" ringing the main dome to distribute sideways forces down to the heavy walls of the buildings.
Although complete spheres are not ordinarily used in buildings, they are an extension of the notion of an arch or dome, in which compression is distributed around the sphere. An egg can be surprisingly hard to crack if subjected to balanced compression forces -- try carefully squeezing a hard-boiled egg -- and spheres are often used in the crew-carrying elements of deep-ocean submersibles, since they can withstand extreme pressures.
* Most basic elements of classical building design, like the arch and dome, were in place by Roman times. Major advances in structural design had to wait until the development of large-scale metalworking in the 19th century. Iron and then steel structural elements, with their strength in both compression and tension and their high strength-to-weight ratio, made possible great steps forward in building design.
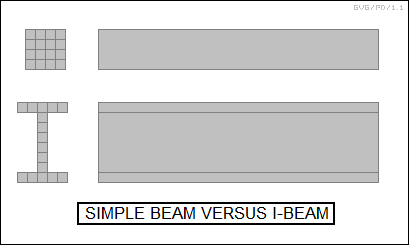
Metal structural beams were generally in the form of "I-beams", which consist of a length of metal with a long flat horizontal plate on the bottom, a similar long flat horizontal plate on top, and a vertical plate connecting the two horizontal plates. A beam is subjected to compression on top and tension on the bottom, and the I-beam is designed to provide the maximum cross-sectional area on bottom and top to resist these stresses.
While metal construction could be applied to traditional structures, it also permitted new sorts of structures, such as the modern skyscraper. The poor strength-to-weight ratio of stone made very tall buildings impossible; metal structural elements allowed buildings to be made much taller. A skyscraper consists of a "cage" of steel girders that supports the floors and the walls. The spectacular explosive demolition of such structures, which usually makes local or even national TV news, is based on the sequential detonation of charges that cut critical structural supports of the cage in a particular order, causing the building to cave in on itself in a heap if the event has been properly planned. Incidentally, explosive demolition is a fairly unusual way to get rid of big structures.
Metal building elements also allowed the development of large truss bridges, with a latticework of metal beams to allow distribution of stresses. It also led to the development of modern suspension bridges -- in which the roadbed is hung from huge cables slung over high towers and anchored to heavy concrete "anchors" at each end -- and "cable-stay" bridges -- in which the roadbed is held up by cables connected directly to the towers.
Concrete was around in Roman times, though the recipe was lost in the Middle Ages and not rediscovered until the 19th century. Modern building techniques make it far more useful than it was to the Romans. Using steel reinforcing rods, it is commonly used for foundations, walls, and other structural elements under compressive loads. However, "prestressed" concrete elements can also be used to handle tension loads that would cause ordinary reinforced concrete to crack. A prestressed concrete structural element is cast in a frame that supports steel cables under tension and laced through the concrete. When the concrete hardens or "cures", the frame is removed, and the tension of the cables within the concrete matrix prevents it from cracking under tension loads.
* There is a balance in the design of structures in the number of structural elements required. Reducing the number of elements reduces complexity, generally reducing the labor of assembly and cost. However, reducing the number of elements also usually means larger elements, which may be difficult to handle, and also more prone to damage.
Suppose a dome is made up of curved panels; the fewer the number of panels, the larger the panels, the greater the load each panel has to carry, making each panel more prone to cracking -- and also making replacement of the panels more troublesome. Of course, if there are a very large number of small panels, installing them will be laborious, and trying to make sure the dome doesn't leak in the rain through the seams between the panels may be difficult.
There are cases where the benefits of "subdivision" are obvious. The cables used to hold up a suspension bridge are each made of large numbers of individual strands; the breakage of a few strands has little effect on the strength of the cable as a whole. It is also possible to construct structural elements as "laminates", using layers of materials that are bonded together with adhesives. Plywood is a common example of a laminate, and panel structures may be made as "sandwiches", with a lightweight core and stiff surface paneling, providing an improved strength-to-weight ratio. Simple corrugated cardboard is a common example of such a sandwich material; much the same approach can be used with metal panels as well, with a corrugated or honeycomb fill. However, laminates do present the hazard of becoming separated or "delaminating" under stress.
Similar principles apply to the types of "composite" materials that consist of threads of one material embedded in a matrix of another material. Examples include glass or graphite fibers embedded in plastic, or "whiskers" of silicon carbide embedded in metal. Any failure of a few threads doesn't do much to undermine the integrity of the structural element made of the composite, and the threads prevent the propagation of cracks. Work is also underway on incorporating sensors in composites in the form of threads to give indication of when a structural element is about to fail, but such "smart" materials are not in common use yet.
BACK_TO_TOP