
* This chapter follows up the discussion of the physics of solids by providing a survey of the mechanics of liquids and gases.
* Liquids have some properties similar to those of solids, such as color and density, but of course they differ in their ability to flow and to take the shape of any container they are poured into. They possess "viscosity", which is a measure of their ability to flow. A "thick" liquid that is hard to shove through a pipe has a high viscosity, while a "runny" liquid that flows quickly through a pipe has a low viscosity. It is obvious that it is much easier to get vinegar out of a squeeze bottle than honey. Viscosity is related to the concept of "fluid friction": concepts of friction and drag apply to liquids, and a liquid with a high viscosity generates a high level of fluid friction.
Another obvious characteristic of liquids is that a body of liquid will seek a common level. A pond undisturbed by wind may be "smooth as glass", as the saying goes, and it will be perfectly level, at least if it's small relative to the curvature of the Earth. It has to be noted here that in more general terms, the angle of the surface of a liquid will be at a right angle to the direction of the force applied to a liquid, so water in a spinning bucket will tend to "climb up the walls" of the bucket. An undisturbed pond will be flat because it is only subject to the pull of gravity, which is straight down. If pipes of various diameters are stuck through the surface of this flat pond, it only takes a moment's thought to realize that the water level is the same no matter the diameter of a pipe.
Yet another obvious property of liquids is that not only can they flow through pipes, objects can flow through or over them. This leads to the concept of "buoyancy", the tendency of objects to float or sink in a liquid. This is unsurprisingly due to the density of the object relative to the liquid. A block of wood is less dense than water and floats on water, while a rock is denser than water and sinks.
The sunken rock will displace a volume of water equal to the volume of the rock. The floating block of wood has a slightly subtler behavior. It will sink into the water under the influence of gravity until it displaces a volume of water equal to its own weight. At that point, it will reach an equilibrium of forces and sink no further. This is known as "Archimedes' Principle", since it was devised by the Hellenic scientist Archimedes (287:212 BCE). The forces supporting this floating block of wood will focus upward and inward on it, summing to a point known as the "center of buoyancy". The center of buoyancy is always above the center of mass of a floating object; the farther the distance between the center of buoyancy and the center of mass, the more stable the object -- that is, the less its tendency to capsize.
According to tradition, Archimedes discovered this fact while getting into a bathtub, and used it to determine for the authorities if a crown being sold by a metalsmith was actually made of gold or a debased metal. Archimedes weighed the crown, then determined its volume from the amount of water displaced, and from that determined its density, which could be compared with that of pure gold. The story says the metalsmith was found guilty and executed, but the tale is probably a myth: it is a bit unlikely that Archimedes, using the instruments available to him, could have performed the required measurements with enough accuracy to have detected a fraud unless the debasement was so gross that it would have been obvious by simply inspecting the crown.
One simple example of the practical application of Archimedes' principle is the "Plimsoll line", which is a marking painted on the hull of a vessel in the form of a circle or diamond cut by a horizontal line. If the ship is sitting so low that the Plimsoll line is underwater, the ship is overloaded. Calibration marks are also painted alongside the Plimsoll line, since the density of water changes between fresh water and salt, or warm water and cold, altering how deeply a vessel sits in the water even when its tonnage doesn't change.
Another interesting example is provided by the question: if all the ice at the North Pole melted, how much would the sea level rise? From a simple consideration of buoyancy, the answer is: not at all. The polar ice displaces a mass of water equivalent to itself, and so when it melts, there is no overall change in the water level. Of course, the ice melting off of Greenland and Antarctica would raise the sea level, and there's also the consideration of the extremely unpredictable ways that an ice-free Arctic Sea might affect global climate.
Incidentally, if a denser liquid is poured into a less dense liquid, as long as the two liquids don't have a tendency to mix, the two will separate, with the less dense liquid on top and the denser liquid on bottom. The classic example of this is oil and water.
* Considerations of buoyancy govern the operation of a submarine. A submarine cruising on the surface of the ocean has an average density somewhat less than that of water. To submerge, it has to take in water in "ballast tanks", increasing its density to more than that of water and causing it to sink. To rise again to the surface, it has to purge the ballast tanks by blowing air into them, forcing the water out and lowering the submarine's density.
Once underwater, a submarine needs to maintain a density comparable to that of water so that it will not tend to either rise or sink. This issue is somewhat complicated by the fact that the submarine's hull is compressed as the vessel dives deeper, reducing the volume of the hull and so increasing the submarine's density. In any case, once the submarine reaches the desired cruise depth, it can then maneuver freely by essentially "flying" underwater, using the "diving planes" or "foreplanes" that are mounted on nose or the "sail" (what's sometimes called the "conning tower") of the submarine, along with the "tailplanes", which are generally arranged in a vertical cross pattern.
However, there is an added complication for a submarine moving underwater. It is not firmly supported, and so if its center of gravity shifts from the middle of the vessel, it will tend to tip down or up, making it difficult to control. This issue, known as "trim", was a particular problem for early submarines. It was solved by adding an additional set of "trim tanks", in addition to the ballast tanks. There is a trim tank in the forward section of the submarine and a trim tank in the rear section of the submarine, with trim maintained by adjusting the relative amounts of water in these tanks.
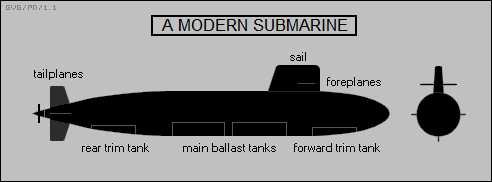
It takes a bit of time to pump water to shift trim, and so in World War II submarine warfare movies there is often a scene where the sub has to crash-dive, and all the crew that can be spared dash forward in a breakneck fire drill through the hatches to make the submarine nose-heavy.
BACK_TO_TOP* Although it is not intuitively obvious, the buoyancy of the submarine does not change in any significant way, no matter how deep it goes. Water is essentially incompressible, and its density is effectively the same at any depth. Drop an iron block into the ocean and it will continue to sink at its terminal velocity -- a concept that applies in liquids just as it does in gases -- all the way to the bottom.
However, there is a limit to how deep a submarine can go, which is imposed by "water pressure" -- the weight of the water above the submarine, which increases linearly with depth. Doubling the depth doubles the pressure. There's nothing particularly tricky about this idea. Suppose Bob has a set of identical concrete blocks, and proceed to stack them up one by one on top of each other. Of course, the force per unit area on the bottom of the stack grows linearly with each block that is added. There is no difference if he stacks up containers of water instead of concrete blocks, or for that matter adds uniform increments of water to a single tall container.
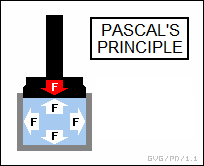
What is not quite so intuitive is that the water pressure is the same in all directions. Suppose Bob applies pressure to the top of a tank of water; then, ignoring the increment of pressure added by the water in the tank as it gets deeper, the pressure of the water against the sides and bottom of the tank is exactly the same as the pressure on the water on top of the tank. This is known as "Pascal's principle", Pascal having published the concept in 1647.
One way to understand Pascal's principle is to understand the operation of a hydraulic jack. Suppose Bob has a tank filled with water, with two tubes containing pistons fitted into the top. One tube has a cross-sectional area of 10 square centimeters, while the other has a cross-sectional area of 100 square centimeters. If he exerts a downward force on the piston in the small tube, the transmission of water pressure on the piston in the big tube will result in an upward force ten times greater.
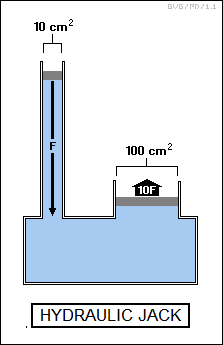
In other words, this arrangement gives Bob a mechanical advantage of 10:1. As with levers and screw jacks and so on, of course he doesn't get something for nothing. A simple consideration of the relative volume of water moved from the small tube to the big tube in this example shows that the piston in the big tube only moves a tenth of the distance upward that Bob shoves the piston in the small tube down.
Another aspect of Pascal's principle is that it accounts for the buoyancy of a floating object, as discussed in the previous section. It is the force of pressure, exerted upward against the floating object, that prevents it from sinking further. Once the volume of water displaced equals the weight of the object, the force of water pressure will then support that object.
* In the definition of Pascal's principle above, the assumptions were that the surface of the tank was under heavy pressure and the tank was not very deep, meaning the pressure was almost the same at the top and bottom of the tank, and the difference could be ignored.
For water of any real depth, the increment of pressure caused by the accumulated weight of water as the depth increases is of course not negligible. Water has a mass of a tonne (1,000 kilograms) per cubic meter, and so on Earth, where the gravitational acceleration is 9.81 meters per second, a cubic tank of water a meter on a side exerts a force of 1,000 * 9.81 = 9,810 newtons on the square-meter base, or 9.81 kilopascals. If Bob keeps the sides of the base the same size, but doubles the height to two meters, the pressure grows linearly to 19.6 kilopascals. If he goes up to three meters, the pressure goes up to 29.4 kilopascals. The water pressure on the sides of the tank increases linearly from zero at the top to the same as the bottom when it reaches the bottom.
However, let's suppose Bob has a tank of water that's a meter high, a meter wide, and three meters long. This tank has a volume of three cubic meters. Is the bottom then under 29.4 kilopascals of pressure?
No, of course not. Pressure is force per unit area. He's increased the volume by a factor of three, but he's also increased the area of the base by a factor of three, and so the pressure remains the same as it was for the one-cubic-meter tank. The pressure is due to the weight of water pressing down only in the vertical direction. That means that it doesn't matter what size the base of the tank is. As long as the water in it is a meter deep, the pressure on the bottom in 9.8 kilopascals.
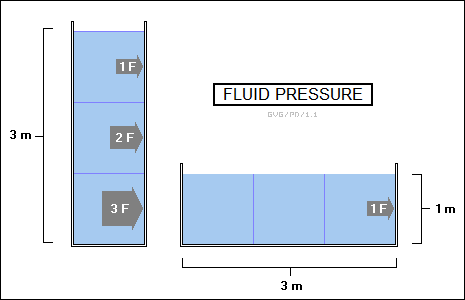
This is more or less intuitive. What is not so intuitive is that, as dictated by Pascal's principle, water pressure is exerted in all directions, and so a dam has to be just as strong to hold back a body of water that extends, say, only 10 meters behind the dam, as it must be to hold back a body of water of equal depth that extends 100 kilometers behind the dam. The depth is the only real determinant of fluid pressure.
There are two basic forms of dams: "gravity" dams, which simply use great mass to hold back the water, and "arch" dams, which are built in narrow rocky canyons in the form of a horizontal arch, which transfers the massive load of the water to the canyon walls. Some dams may use both mass and an arched configuration to ensure structural stability.
* Obviously, the pressure of a liquid is equivalent to potential energy. If Bob installs a valve at the bottom of a tank and opens it, then the water will pour out in a stream and will be able to do work, for example by turning a water-wheel.
That should not be surprising. A solid mass held at a height has potential energy due to its elevated position in a gravitational field, and the only difference between that and a liquid is that the liquid is in effect a continuous series of masses held at a continuous range of heights. This makes calculation of the precise value of potential energy of the liquid in a tank a bit tricky. We won't do that here, but the important thing is to realize that water pressure is equivalent to potential energy, in the same way that the tension of a compressed spring is equivalent to potential energy.
Now let's suppose Bob decides to tap this potential energy by opening the valve on the bottom of the tank. Water floods out in a stream. Since the water is now moving, it has kinetic energy. Of course, the higher the pressure at the valve, or equivalent the greater the height or "head" of water above the valve, the greater the kinetic energy of the flow and the greater its velocity. This is known as "Torricelli's principle", after the Italian physicist Evangelista Torricelli (1608:1647).
Since conservation of energy says that Bob can't get something for nothing, this increase in kinetic energy must be obtained by a decrease in potential energy. As water pressure is equivalent to the potential energy of a liquid, this means that the pressure must decrease as well.
In other words, the faster a liquid moves, somewhat counterintuitively the more its pressure decreases. However, it's not so different in concept from Bob firing a ball out of a spring-loaded toy gun: the spring tension is released and converted into the kinetic energy of the ball. The same effect is observed when water or another liquid passes from a pipe with a wide cross-section into a pipe with a narrow cross-section. For a given rate of liquid flow, measured in liters per second, the velocity of the flow, measured in meters per second, has to increase if the pipe diameter decreases to maintain the flow. In mathematical terms:
_________________________________________________________________________
liquid_flow_rate =
cross_section1 * velocity1 =
cross_section2 * velocity2
_________________________________________________________________________
The increased velocity of the liquid flow in the narrow section of pipe will result in a decrease in liquid pressure. The following illustration demonstrates this principle, which is known as the "Bernoulli effect", after the Swiss physicist and mathematician Daniel Bernoulli (1700:1782).
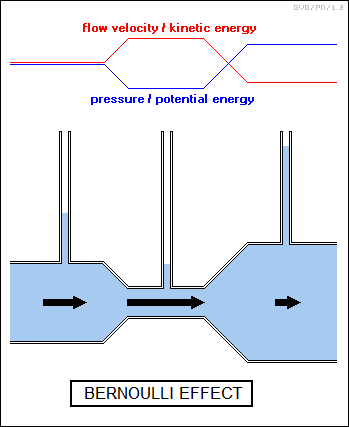
This illustration shows the pipe as horizontal. Of course, if it weren't, the liquid would flow "downhill" and pick up additional kinetic energy by the simple act of falling under gravity, complicating the analysis.
* On a small scale, liquids can demonstrate behavior that would seem bizarre on a larger scale, due to attractions between the molecules of the liquid. For example, people can't walk on water, but insects like water-striders can. The intramolecular forces set up by water create "surface tension" that prevents a light object from simply falling right through the surface, even if it's denser than water. Similarly, the adhesion of water to, say, glass surfaces will cause it to crawl up into glass tubes stuck into the surface of the water. This sort of "capillary action" is greater for tubes with very small diameters than it is for tubes with very large diameters. Again, this is due to a scaling effect, since doubling the diameter of a tube only doubles its circumference and the area of its glass walls, while the cross-sectional area and the amount of water that is to be lifted increases by four times.
One interesting application of these phenomena is the "restartable" rocket engine. A rocket engine that has to be restarted in space has to deal with the problem that in free-fall, the propellants won't flow down out of the tank to the engine, since there is no "down". There are various ways to deal with this problem; one ingenious scheme relevant to the current discussion is to fit the fuel tank with a set of internal grids of finer and finer spacing towards the bottom of the tank. The grids set up a "wicking" action that pulls the propellant to the bottom of the tank.
BACK_TO_TOP* Gases have much in common with liquids. They can flow, for example, and less dense objects will float. Gases also are subject to considerations of pressure like to those of a liquid; the weight of the atmosphere presses down on those who live at the bottom of it, and this atmospheric pressure drops off as we go to higher ground or fly up into the sky.
I live in a region where the ground elevation is a mile (1.6 kilometers) above sea level, though the ground is flat off to the sunrise, and as a result if I buy food products such as potato chips that are sealed in airtight bags, the bags are puffed out like pillows here. I bought double-pane windows that were filled with an insulating gas from a national company for my house here; these windows had to be made by a plant in the region, since if they had been built at lower altitude and brought up here, the difference in pressure would have caused them to spring leaks.
The atmospheric pressure of the Earth at sea level makes a convenient reference point for discussions of pressure, and one older measure of pressure is the "atmosphere", or 101,325 pascals. This is a somewhat arbitrary measure of pressure, however, and not convenient to work with using metric units, but the value of 100,000 pascals, known as a "bar", can be used as a reasonable approximation -- all the more so because the pressure of air at sea level actually varies with changes in humidity, temperature, and wind conditions.
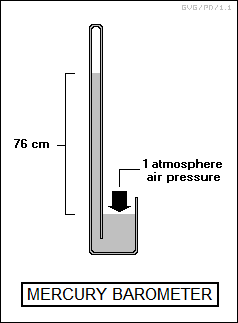
A "barometer" is used to measure atmospheric pressure. A traditional scheme for building a barometer involves a U-shaped tube partially filled with mercury. One end of the tube is sealed and the other is open to the atmosphere. Mercury is squirted into the sealed end of the tube while it's upside down, and when the tube is turned over, the mercury falls down to the bend in the tube, leaving behind a vacuum in the sealed side. Air pressure will push the mercury up into the vacuum, and the height of mercury on the sealed side will provide an indication of atmospheric pressure. The mercury will be 76 centimeters higher in the sealed side of the tube than the open side of the tube at a standard atmosphere of pressure. Of course, since pressure is force per unit area, it doesn't matter how wide the tube is, as long as its diameter is constant.
This scheme was discovered by Torricelli in 1643, and a now-disused measure of pressure named the "torr", equivalent to the displacement of a millimeter of mercury under standard conditions, was defined in his honor. Naturally, a standard atmosphere of pressure is equivalent to 760 torr, or 76 centimeters of mercury.
A more modern approach is to use a metal bellows that has been evacuated. The bellows is connected to an indicator needle through some mechanical arrangement that amplifies any minor motion in the bellows, and as the bellows flexes under changes in pressure, the needle moves to give the pressure value on the indicator scale. This device is known as an "aneroid barometer". If the indicator scale is calibrated to give altitude instead of air pressure, the device is called an "altimeter".
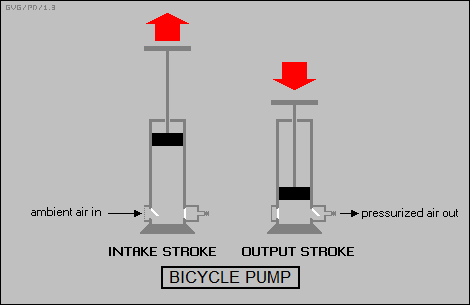
Manipulating the pressure of air or other gases is the basis of "pneumatic" technologies. The most basic pneumatic device is the hand-driven air pump or "bicycle pump" as it's sometimes called, which involves a cylinder with a piston that is moved up and down by muscle power. There are two valves in the cylinder, an "input" valve that opens inward under a pressure difference and an "output" valve that opens outward under a pressure difference.
Pulling up the handle on the pump creates lower pressure inside the cylinder, which causes the input valve to pop open, with ambient air entering to eliminate the pressure difference. Pushing down on the handle creates higher pressure inside the cylinder, forcing the input valve closed and popping the output valve open to push air into the tire or whatever.
* The notion of the mercury barometer leads to the concept of the "siphon", in which a liquid such as water can be driven from a reservoir to an outlet through a pipeline over a hill or other obstruction. This vertical diversion is called a "siphon", and it works as long as two conditions are obeyed: the outlet has to be lower than the surface of the reservoir, or in other words water will still only flow downhill overall, and the siphon has to be filled with water before the scheme will work.
This looks like a problem in hydraulics, and it is, but the principle behind it is the same as that behind the mercury thermometer: the column of water flowing up the siphon is supported by the air pressure pressing down on the surface of the reservoir. When water flows out the outlet side of the siphon, it creates lower pressure, and so water on the inlet side of the siphon is driven upward. That's why the siphon has to be filled before the siphon effect will work: if the outlet side of the siphon was open to the air, the water level in the input side of the siphon would be exactly the same as it was in the reservoir.
There is a limit to the height or "crest" of the siphon above the reservoir level, depending on the density of the liquid and the air pressure above the reservoir. As mentioned, one atmosphere of pressure will lift mercury to a height of 76 centimeters, and since mercury is about 13.5 times more dense than water, one atmosphere of pressure on a reservoir should lift water about 13.5 x 0.76 = 10.26 meters. This seems like a shallow crest for getting water over the top of a tall hill, but it must be remembered that the crest is relative to the water level in the reservoir, not relative to the bottom of the hill. Water reservoirs are often sited on high ground; the pipeline from the reservoir may drop down into a valley and then back up over a hill, but the crest of the hill will be about the same height or lower than the reservoir level.
* Buoyancy issues are as relevant in gases as they are in liquids. For example, if a balloon is filled with a light gas such as hydrogen or helium, it will have a lower density than the ambient atmosphere and tend to float up.
There is also the phenomenon of "lift" in heavier-than-air machines like aircraft and helicopters. There are misconceptions on how lift actually works, the biggest being that it is due to the Bernoulli effect, an error that actually pops up in elementary physics books. As the story goes, the wings of an aircraft have a curved cross-section, with a greater curvature on the top than on the bottom. Air flowing over the top of the wing has a longer path, and so its flow over the wing is more rapid. This means that the pressure on top of the wing is less than that on the bottom, and the effect is to provide a net upward force known as "lift" that keeps the machine flying.
The problem with this scenario become immediately obvious when the question is asked: "So how can aircraft fly upside down?" They don't normally -- since it's uncomfortable for the pilot, and some piston engines don't work well upside down -- but any good flight demonstration team like the US Air Force Thunderbirds flies their jet fighters upside-down as a regular practice, and the machines don't immediately fly into the ground. The fallacy with the Bernoulli effect argument is that it assumes the airflow over the top of the wing has to maintain mass flow with the airflow over the bottom of the wing when it isn't constrained to do so. The Bernoulli effect may have some effect on lift, but it's not the primary mechanism for the phenomenon.
The actual reason for lift is Newton's third law of motion. In flight, a wing is held at an "angle of attack (AOA)" upward of the direction of airflow, with the airflow striking the bottom surface and being deflected downward as "downwash". The downward velocity component of the downwash provides a reaction to force the wing (and the aircraft connected to it) upward. The need to maintain AOA relative to the airflow does not mean the aircraft has to fly nose-up all the time; the wing may be fixed to the fuselage at a predetermined AOA relative to the aircraft's flight axis.
As far as this description goes, a simple flat wing would work as well as any other, so why is a wing typically built with a curved upper surface? The trick is that such a wing would produce a good deal of turbulence over the top of the wing, causing "buffeting" as well as some "upwash" of the airflow, which would tend to force the aircraft back down. Due to some subtle features of fluid flow -- discussed in a bit more detail below -- the airflow tends to hug the curve of the upper surface, which means that it leaves the trailing edge of the wing in a downward direction, also contributing to lift.
The higher the AOA of the wing, incidentally, the greater the drag, and so there's a tradeoff between AOA and speed. It is not unusual for an aircraft to have a landing gear configuration that leaves it nose-high, increasing the AOA until the aircraft gets off the ground and starts flying level. A high AOA is particularly important for carrier take-offs and landings, since the aircraft has to get up or down in a short space. A number of British carrier jets of the 1950s and 1960s were actually launched off carrier catapults strapped down so their nosewheel was in the air to ensure a high AOA. The US Navy Vought F-8 Crusader fighter had a wing that hinged upward for take-offs and landings to permit a high effective AOA, while giving the pilot a good view forward.
Such considerations of lift show that a conventional aircraft, even though it can in principle fly upside down, isn't as efficient in flight when doing so, having to maintain a nose-up attitude to ensure a usable AOA. Stunter aircraft may have no fixed AOA, and wings that are curved on both sides.
* An aircraft has "flight control surfaces" that modify the airflow to control the machine's direction. There are moving panels at the trailing edge of each wing known as "ailerons" that are pivoted in an alternating fashion -- on one side up, on the other down -- to allow the aircraft to "roll". There are "elevators" at the trailing edge of the horizontal tailplane that are pivoted together to cause the aircraft to "pitch" up and down. Finally, there is a "rudder" at the trailing edge of the vertical tailplane that can be pivoted to cause the aircraft to "yaw" back and forth.
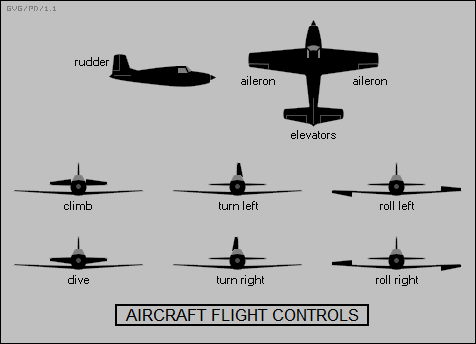
These are the "basic" control surfaces, but there are many variations. For example, many tailless aircraft, usually delta-winged machines, have an "elevon" on each wing, with both moved up or down to provide elevator pitch control, or moved in opposite directions to provide roll control.
Tailless flying wing aircraft that don't have a tailfin, such as the B-2 Stealth bomber, have "rudderons" that are split top and bottom on the outer rear edge of the wing. Both rudderons can be opened up top and bottom on one side to cause the aircraft to turn, or can be opened up top and bottom on both sides of the aircraft to act as airbrakes. An elevon is fitted on each half of the wing inboard of the rudderon to provide pitch and roll control.
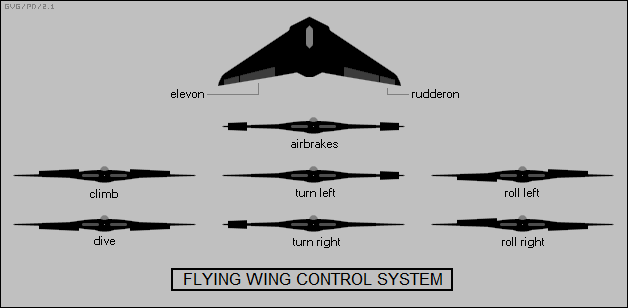
Incidentally, moving the rudderons away from their neutral position greatly increases the B-2's visibility to radar, so when it is flying into a combat area it steers by adjusting engine thrust, though this is more troublesome and less effective than using rudderons. Aircraft may also have a number of auxiliary control surfaces:
Like a submarine, an aircraft has to maintain trim. This is obvious in the case of cargoes, which clearly can't be loaded onto a cargo plane in an unbalanced fashion, and the crew of a large cargo aircraft will generally include a specialist called a "loadmaster" who ensures that the cargoes are loaded in a methodical fashion and balanced properly -- incidentally, maritime cargo vessels also have loadmasters to ensure efficient stowage of cargo, and reduce the hazard of capsizing due to an unbalanced load. Aircraft trim is less obvious in the important case of fuel management. Usually aircraft designers will try to put fuel tanks at the center of gravity of an aircraft, but an aircraft may have several fuel tanks, and care often must be taken to empty the tanks in a specific order, or the aircraft may become unbalanced. This was done manually by the pilot in the past, but now sophisticated aircraft have automatic systems to ensure the proper sequencing.
Since an aircraft will always have slight imbalances, instead of having the pilot try to compensate for trim faults by keeping the control surfaces slightly activated at all times -- which would be very tiring -- traditionally aircraft have featured small control surfaces called "trim tabs" that can be set to a fixed position using a dashboard knob to keep the machine flying level. Some aircraft may instead use knobs to introduce a slight bias in the aircraft's flight control surfaces.
BACK_TO_TOP* The discussion to this point on the flows of liquids and gases -- which can be lumped together as "fluids", meaning both can flow -- has been simplified by assuming the flows aren't viscous -- that is, subject to friction forces -- and are incompressible. These are reasonable assumptions for a simple analysis, but the real world can be substantially more complicated.
Formal studies of the effects of viscosity on fluid flow began in the middle of the 19th century, leading to the invention of equations for describing the viscous flow of an incompressible liquid; the equations were developed independently by Claude Louis Marie Navier (1785:1836), a French engineer, and Sir George Gabriel Stokes (1819:1903), a British mathematician, and so these rules are known as the "Navier-Stokes equations".
They're not simple equations, and in fact they are only fully solvable for simple scenarios. Bernoulli's principle no longer strictly applies since the viscous friction depletes energy from the flow, resulting in a pressure drop along the pipe. At the outset, it was thought that this pressure drop would increase in direct proportion to the flow velocity -- that is, double the flow velocity and the pressure drop doubles as well -- but experiments showed that this was only true up to a certain threshold. Beyond that threshold, the pressure drop increased with roughly the square of the flow velocity.
This hinted that there were two different processes at work, which was demonstrated by Osborne Reynolds (1842:1912), a professor at the University of Manchester in Britain. Reynolds devised an apparatus in which he could observe the flow of dye in water pumped through a tube. He observed that the dye would flow straight for a distance, what was called "laminar" flow, and then break up into a tangle of eddies, what was called "turbulent" flow. This phenomenon can be observed by watching smoke float up off the tip of a lit cigarette: the smoke will rise for a space and then break into a tumble of coils. Incidentally, turbulent fluid flows are an example of a chaotic system.
In any case, the drag of the flow increases dramatically when the flow changes from laminar to turbulent. Reynolds was able to devise an equation that factored in the flow velocity, the density of the fluid, the viscosity of the fluid, and the length of fluid flow to return a value that would indicate when the flow changed from laminar to turbulent. The "Reynolds equation" is given as follows:
fluid_velocity * length_of_fluid_flow * fluid_density / fluid_viscosity
The value returned by the Reynolds equation is known, to no great surprise, as the "Reynolds number (RN)". If the RN is less than 2,100, the flow will always be laminar. It doesn't necessarily switch to turbulent just above that value, but it becomes increasingly unstable and likely to shift to turbulent as the RN increases beyond 2,100.
One of the interesting features of the RN is that fluid flows with similar RNs behave in much the same way, no matter if the fluid is air or water or whatever. A sailboat moving at low speed in a dense fluid like water has much the same behavior in terms of fluid dynamics as an aircraft moving much faster in a thin fluid like air. This has a major, though not obvious, implication for issues of scaling in aircraft design. The smaller an aircraft gets, the greater the effective viscosity of the air.
To a gnat, the air feels thick and viscous, and flying is more like swimming -- in fact, the smaller the creature, the less bother it is to get into the air, and small spiders will sometimes migrate by simply throwing out a thread of silk to the wind. Researchers working on tiny robot aircraft have finding out that conventional aircraft designs are not very workable at such small scale, and they have gravitated towards unusual designs, such as circular flying wings, or even "ornithopters" that flap their wings to fly.
* The complexity of the analysis of viscous flows meant that scientists and engineers really needed to obtain simplified but still workable methods. In 1904, the German engineer Ludwig Prandtl (1875:1953) observed that flows could be often be separated into two regions: a thin region known as the "boundary layer" close to the surface over which the flow passes and where the viscous effects are concentrated, and the region of flow above the boundary layer where viscous effects could be disregarded.
It is this viscous boundary layer that causes the airflow over the top of a wing to follow the curve of the wing -- in effect, it causes the airflow to stick to the wing. At low speeds, the boundary layer will tend to "separate" from the wing and ruin lift, and so a number of combat jets were built with a "blown flaps" or "boundary layer control (BLC)" scheme in which jet engine bleed air was blown over the top of the wing or the flaps to ensure that low-speed separation didn't occur.
The boundary layer can also be a nuisance for combat jet aircraft. The engines of such aircraft require a continuous large airflow to provide a high level of thrust, and if the engine intakes are close to the aircraft's fuselage they may swallow the viscous ("stagnant") boundary-layer air, choking off airflow and engine power -- even leading to "engine stall" that can "flame out" the engine or, in the worst case, damage it. Such aircraft often have a "splitter plate" between the front of each engine intake and the fuselage; these plates are set slightly off from the fuselage and prevent the boundary-layer air from being sucked into the inlet.
* Assuming that a fluid is incompressible is appropriate if the fluid is a liquid, but it can lead to drastically wrong conclusions when the fluid is a gas. Even assuming nonviscous laminar flow, Bernoulli's law only really applies to slow-moving gas flows; if the gas flows are rapid, compression comes into play, leading to distinctly different behavior. Analysis of a compressible flow is too tricky to be discussed in detail in this document, but a simple example will illustrate the principles involved.
Consider a standard rocket nozzle: it can be modeled as a cylinder that leads to a constriction, known as the "throat", which leads into a widening "exhaust bell" open at the end. Hot gases flowing down the hit the throat, where the velocity picks up and the pressure falls, roughly as it would in a fluid, though compression occurs as well. Once the hot gases exit the throat and enter the widening exhaust bell, they expand rapidly, and this expansion drives the velocity up while the pressure continues to fall -- exactly the reverse scenario of what would occur if a fluid passed through a constriction into a widening bell.
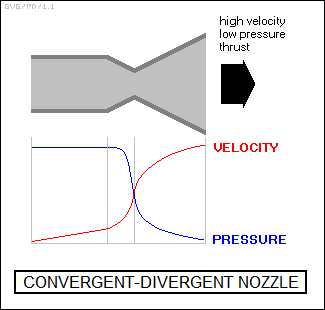
A standard rocket nozzle is designed to provide optimum thrust for a certain range of altitudes and atmospheric pressures. High-performance jet combat aircraft must operate effectively over a wide range of conditions, and so they have exhausts whose geometry can be varied depending on need.
A fully "authentic" computer simulation of a real-life gaseous flow that takes into consideration viscous effects, turbulence, and compression can demand serious computing horsepower. There is a complicated interaction between all the facets of the simulation -- which can get even more complicated if chemical transformations take place in the stream.
One aspect to the complexity is that the pressure, volume, and temperature of a gas are closely related to each other. This leads to a consideration of concepts of "temperature" and "heat", which are somewhat devious to define. Although this document has mentioned temperature effects in a casual fashion, to go much further requires a more detailed discussion. Similarly, although matter can often be converted between solid, liquid, and gaseous forms through changes in temperature, that also requires a more detailed look. These issues are discussed in the next chapter.
BACK_TO_TOP