
* This chapter elaborates on basic concepts of orbital mechanics by presenting some interesting examples and applications of orbital mechanics.
* The previous chapter discussed how the Earth and Moon are tidally locked, with the Moon always keeping its same face to Earth. Most of the major moons in the Solar System are also tidally locked to their planets. In the Pluto-Charon system, both planets are tidally locked to each other, so Charon hangs overhead in Pluto's sky in the same place at all times. The energy of rotation of the two worlds was dissipated in internal heating due to tidal stretching effects. This tidal heating appears to be a significant process in the internal heating of Jupiter's volcanic moon Io, which is relatively close to the giant planet and so is subjected to strong tidal forces. The surface of Io is covered with huge sulfurous volcanic flows.
It was once thought that the planet Mercury was tidally locked to the Sun, so that it kept one face eternally faced to the Sun and the other in darkness, one side burning and the other side freezing. This was found to be not exactly the case in the 1950s. It is in a "resonance" where it turns three times for every two orbits around the Sun, in what is known as a "metastable" state. If Mercury kept one face always to the Sun, it would be in a minimum energy state, but to get out of its 2:3 resonance state it would have to receive some sort of increase in rotational energy, possibly through a collision with another large body. Until something like this happens, Mercury's rotation will remain as it is, something like a stone that's been caught on a ledge after falling halfway down a cliff instead of dropping all the way to the bottom.
* Due to the N-body problem, the gravitational interactions between all the planets in the Solar System are complicated and difficult to predict over the long run. At a coarse scale, the gravitational interactions of the Solar System are dominated by the Sun, which is over 330,000 times more massive than the Earth; and Jupiter, which is about 320 times more massive than the Earth. The second biggest planet, Saturn, is only about 95 times the mass of the Earth, and all the other planets are much smaller than Saturn. Jupiter has well more than twice the mass of all the other worlds in the Solar System combined.
Jupiter's gravitational influence led to the creation of the asteroid belt, since it prevented the formation of any single large body at that location. Interestingly, there are empty "bands" in the asteroid belt that correspond to asteroid orbits that would have a some sort of synchronization or resonance with the orbit of Jupiter. Any asteroid in such an orbit is quickly pulled out of it by periodic gravitational tugs from Jupiter.
Another consequence of Jupiter's gravitational influence is that objects straying into the two locations in its orbit that are equally distant from the Jupiter and the Sun tend to stay there. These orbital positions are known as "libration points" -- note the spelling, it's easy to misspell as "libation" -- or sometimes "Lagrangian points" after the French mathematician Louis Lagrange (1736:1813).
Lagrange performed an analysis of the gravitational interactions of two bodies in orbit around each other to identify positions where objects would remain stationary relative to the bodies. He actually discovered five such stable positions, now known as "L1" through "L5", roughly laid out as follows relative to two masses of the same size:
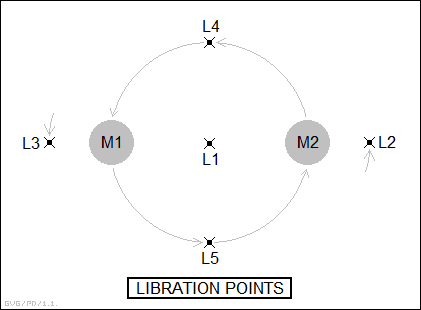
L1, L2, and L3 are in unstable equilibrium, only stable in the sense that a ball balanced on a rod is stable. L1 is located between the two bodies, and an object placed there will fall towards one or the other if disturbed. Objects at L2 and L3 are at a precise orbital radius around the two bodies where they keep pace with the orbits of the bodies. At a lower radius, the objects will have a faster orbit and move ahead, while at a higher radius, they will have a slower orbit and fall behind.
In contrast, the equidistant positions, L4 and L5, are in stable equilibrium, just as much a ball caught in a depression is in stable equilibrium. If any object caught at these locations is disturbed and begins to move out of them, the forces of the two bodies tend to nudge it back into place. The L4 and L5 positions in Jupiter's orbit have trapped a number of asteroids, referred to as "Trojan asteroids".
* One effect of the interactions between the planets is to rule out the existence of a "Counter Earth", a plot device found in old science-fiction stories. The idea is that there is another planet on the other side of the Sun exactly opposite to Earth that remains eternally unseen. This would seem implausible in the first place, since it's obvious there are no other "counter planets" such as a "Counter Mars" or "Counter Jupiter". The Earth is on the opposite side of the Sun relative to every other planet at some time or other, and no counter-worlds for Mars or Jupiter have been seen. Furthermore, a Counter Earth would be a bright object, and no deep space probe has ever spotted such a thing with its telescopic cameras or other sensors.
In reality, a Counter Earth is impossible, since even if such a world were magically created right now, the unbalanced interactions of all the other planets on the Earth and Counter Earth would disrupt the neat symmetry; ultimately the Counter Earth would likely end up in one of the libration points in Earth's orbit, equidistant from Sun and Earth, where it would be easily seen from Earth -- and would effectively rise or set at the same time each day.
The Earth does actually share its orbit, literally more or less, with a handful of small asteroids. The discovery of the first of these "Earth co-orbital" asteroids, designated "3753 Cruithne", a Celtic name pronounced "crou-EEN-ya", was announced in 1997. 3753 Cruithne's orbit is known as a "horseshoe" orbit, which describes the path its orbit traces out if the Earth is regarded as stationary.
To visualize the simplest form of a horseshoe orbit, imagine an asteroid that is orbiting slightly inside the orbit of the Earth. As it is in a tighter orbit, it is orbiting faster than the Earth, and gradually catches up to it.
This is where things get interesting. Once the asteroid gets close to the Earth, the Earth's gravity nudges it into an orbit outside that of the Earth's. The asteroid is now moving more slowly than the Earth and falls behind. Eventually, the Earth will catch up to the asteroid in this exterior orbit and shunt it back to the original interior orbit. Since it is moving faster than the Earth in the interior orbit, it moves away from the Earth, to eventually come around behind it again ... and repeat the cycle once more. From the point of view of the Earth, the asteroid's path forms a "horseshoe", continuously approaching the Earth and being sent back on its path again. As the Earth and the asteroid have similar orbital velocities, it takes centuries for the asteroid to complete a single horseshoe orbit.
3573 Cruithne's orbit actually has a slightly different inclination and orbital eccentricity to that of the Earth, and so from the point of view of the Earth, the asteroid makes a series of many kidney-bean-shaped spirals along its horseshoe path. It performs one such spiral every year, with each spiral taking it one step towards or away from the Earth, and the cycle takes a total of 385 years. Its orbit actually can overlap that of the Earth, at least as seen from above the plane of the Earth's orbit, but due to the different orbital inclinations of the two worlds it cannot come even as close to the Earth as the Moon.
There are several other Earth co-orbital asteroids; a few do not have horseshoe orbits, instead being "quasi-satellites" of the Earth. The intersection of their orbits with the Earth's places them in an effective orbit around our planet, though they are not gravitationally bound to the Earth. In time, they are likely to move out of the quasi-orbit.
* The gas giant outer planets have elaborate moon and ring systems that provide interesting examples in orbital mechanics. For one example, Tethys, a moon of Saturn a bit over 1,000 kilometers in diameter, has two small co-orbital moons, Telesto and Calypso, both a few tens of kilometers in diameter, which are at the stable libration points, equidistant from Tethys and Saturn.
Saturn also has a set of co-orbital moons, Janus and Epimetheus, both with diameters of a few hundred kilometers, that have a relationship very similar to that of the Earth with its co-orbital asteroids. The orbits of Janus and Epimetheus are not exactly the same, being about 50 kilometers apart. Of course, the moon in the lower orbit has a faster angular velocity than the moon in the higher orbit, and so the two moons draw together. Once about every four Earth years, they pass each other -- and trade orbits, with the moon in the lower orbit going into the higher orbit and the moon in the higher orbit going into the lower orbit. Astronomers were a bit confused for a few years until they finally figured out what was going on.
Resonances between the orbits of moons in these systems are known as well. For example, Saturn has two moons named Dione and Enceladus that have a 1:2 resonant relationship, with the outer moon Dione performing one orbit of Saturn for every two orbits of the inner moon Enceladus.
* A knowledge of orbital mechanics is very useful for the studies of distant star systems. The stars look like points of light in even the largest conventional telescope, and so astronomers have to rely on sometimes very subtle indirect means to determine their distance, size, and true brightness.
This task is simplified if astronomers find a "double star" system, in which two stars orbit around each other. It is possible to precisely time how long the orbit takes through observation. It is also possible to determine how fast the stars are moving in their mutual orbit through changes in the color of their light emission, or "Doppler shift", discussed later.
If the velocity of the stars in their mutual orbit is known and the period of the orbit is known, then the length of the circumference of the orbit can be determined by multiplying the velocity times the period, giving the length of the circumference of the orbit. Comparing the actual size of the orbit against its size as seen from Earth can give a good estimate of the distance to the double-star system.
Furthermore, knowing the size of the orbit and its period gives the combined mass of the two stars, using Kepler's Third Law:
_________________________________________________________________________ orbital_period^2 = constant * orbital_radius^3 _________________________________________________________________________
The constant in this expression is related to the force of gravity between the two stars and so two masses involved, and so the expression can be algebraically manipulated to give:
_________________________________________________________________________ system_mass = constant * ( radius^3 ) / ( period^2 ) _________________________________________________________________________
The constant can be simplified by specifying the orbital radius in terms of the Earth's orbit, or "astronomical unit (AU)"; the orbital period in terms of the Earth's orbital period, or years; and the system mass in terms of multiples of the mass of the Sun. For the case of the Earth-Sun system, this gives the system mass, the radius, and the period all as 1, and so the constant has to be 1 to get the right result. Of course, for the Earth-Sun system the mass of the Earth is negligible compared to that of the Sun.
Suppose a distant star system is discovered featuring two stars with an orbital radius of 2.3 AU and an orbital period of 1.2 years. This gives the combined mass of the two stars as:
( 2.3^3 ) / ( 1.2^2 ) = 8.45 solar masses
Locating the center of the mutual orbit will allow the proper masses to be applied to each of the star: if the center of the orbit is halfway between the two stars, then each weighs 4.225 solar masses.
BACK_TO_TOP* Libration points are very useful in spaceflight planning. The L4 and L5 locations relative to the Earth and Moon have been promoted as ideal locations for space colonies. Similarly, the Sun-Earth L1 position, a hundredth of the way from the Earth to the Sun, is an ideal location for satellites that observe the Sun; and the Sun-Earth L2 position, 1.5 million kilometers beyond the Earth's orbit around the Sun, is an ideal location for satellites used to perform deep space astronomy.
Several solar observatories have been launched into the Sun-Earth L1 position. At the L1 position, these spacecraft have an excellent view of the Sun that is never blocked by the Earth, and are within easy communications range of the Earth. In August 2001, NASA launched a spacecraft named "Genesis" that was placed there between Earth and Sun to capture particles emitted by the Sun for return to Earth.
In the summer of 2001, NASA launched the "Microwave Anisotropy Probe (MAP)", which was parked in the Sun-Earth L2 position, far beyond the Moon's orbit away from the Sun. There, the spacecraft began mapping low-level energy emissions from the distant Universe, deploying a shield to block out emissions from the Sun and Earth to its back that might disrupt the measurements. Other astronomical spacecraft have similarly been sent to take up station at the L2 position.
* Of course, sending several spacecraft Sun-Earth L1 or L2 position would lead to clutter, and the L1 position has the added difficulty that any spacecraft sitting there is in the full glare of the Sun as seen from Earth. The Sun generates radio noise as well as light, and this creates interference in communications with the spacecraft. The solution to both these problems is what is known as a "halo" orbit, in which a spacecraft performs long, lazy curved loops around the libration point, almost as if the libration point was a celestial body.
A halo orbit is an N-body problem, involving interactions between the probe, the Sun, and the Earth. Early calculations of halo orbits involved a "successive approximation" approach: making educated guesses, running them through a software simulation, and then using the result to get a better guess.
This method was workable but crude. In the 1990s, improved software was developed that essentially mapped out entire ranges of three-body trajectories, known as "manifolds". Paths known as "dynamical channels" can be identified on the manifolds that chart out the course a spacecraft would follow on its own after given an initial push, analogous to the way a ball bearing would meander about on an uneven surface after being given a nudge one way or another.
The Genesis spacecraft, for example, was initially launched into a parking orbit around Earth. A short engine burn then sent it drifting towards the Sun, and three months later another brief burn put into a halo orbit around the L1 position. It then performed a total of four halo orbits, each lasting six months. After the end of the sampling mission, another burn sent the probe on an orbit that brought it all the way back to a halo orbit around L2, where MAP was making its measurements, and then to a close Earth flyby, where Genesis dropped its sample package.
The reason for this roundabout maneuver was to allow the package to be ejected during daylight hours. Since it was to be recovered by helicopter to prevent contamination, it could not be sent back at night. Unfortunately, although the elaborate flight plan went as intended, the capsule did not deploy its parachute after re-entry in September 2004 and crashed into the desert. Some of the payload proved recoverable.
Martin Lo, one of the leaders of the Genesis program, called the elaborate network of manifolds snaking throughout the Solar System the "Interplanetary Superhighway". Jupiter and Saturn also have extensive sets of large moons that set up networks of manifolds on a smaller scale. By exploiting dynamical channels along these manifolds, the probe could maneuver from moon to moon, remaining at each for as long as desired, and then changing position with a slight nudge from its rocket engine.
BACK_TO_TOP* It might be thought from the examples of orbital mechanics shown so far that the motions of heavenly bodies follow a neat, predictable clockwork regularity. This was much the way things were seen in Lagrange's time, but in modern times this is seen as a somewhat misleading impression. Tidy resonances and other orderly arrangements of celestial bodies will occur when relatively large forces can be focused on these bodies in a consistent fashion. For example, the Trojan asteroids are trapped in their orbits by the Sun and Jupiter, the biggest objects in the Solar System and with the most powerful gravity.
Such orderliness is not always the case. As the discussion of software for orbital mechanics shows, the gravitational interactions of all the bodies in the solar system are impossible to calculate with perfect precision, and approximate methods are required in practice. These methods are workable, of course, but they have limitations in their accuracy that can become important over the long term.
The best example is that of the orbits of most asteroids. A set of sightings can be used to obtain the orbit of an asteroid, but over time that orbit will shift in an unpredictable fashion, partly due to the unpredictable gravitational interactions of the asteroid with all the other bodies in the solar system, and partly due to other subtle effects, such as the pressure of sunlight. These little "nudges" on the orbit of an asteroid don't amount to much at any one time, but over a long period they can modify the asteroid's orbit to the point where it is "lost" and has to be "discovered" again.
* This uncertainty in orbital mechanics is a good example of uncertainties in physical systems in general. In an introductory document like this, the focus is on "linear" systems, in which the result of a set of influences on the system is directly proportional to the sum of the influences. Add masses to a box, the total mass of the system is just the sum of the individual masses.
However, physical systems may be "nonlinear", in that the result of the individual influences on the system don't add up in a nice uncomplicated way: a small shift in snowpack can trigger a huge avalanche in a "cascade" process. In the worst case, influences may add up in ways so that the results become impossible to predict over some period of time: influences too small to measure eventually grow and take the system off into some unpredictable direction. Such systems are known as "chaotic".
The best-known example of a chaotic system is the weather. Everybody knows that unless the weather in a location is extremely predictable, the accuracy of official weather forecasts falls off drastically as the forecast is extended into the future. Forecasts are likely to be accurate for the next day, but they are very unlikely to be accurate for a week into the future. Physicists like to describe the instability of the weather with the "butterfly effect", the idea that the movement of the wings of a butterfly in China one day might produce a tornado in Texas a week later. Forecasts can be improved with better computer simulations, throwing more computing horsepower at the problem, but that doesn't eliminate unpredictability, it just pushes it a bit farther out into the future.
Surprisingly, chaotic systems are not completely unpredictable. Once they are isolated from disruptions they may settle into patterns known as "attractors", in which the elements of the system move within certain limits, as if they were "attracted" to that range of paths. There are different specific classes of attractors, such as the "Lorenz attractor", a pattern of paths that looks like the eyes of an owl. It was named after Edward Lorenz (1917:2008), one of the pioneers of modern "chaos theory", who came up with the butterfly effect in the early 1960s. There is also the famous "strange attractor", which is a "fractal pattern". Fractals are geometric figures in which their overall appearance is duplicated at greater levels of "zoom" in on the figure. Natural examples of fractals are clouds, shorelines, and snowflakes.
Chaos theory was something of a scientific fad at one time, being inflated, often along with fractals, into a "new science". That was a bit of an exaggeration since the basic ideas have been around for a century or so, though they have only been investigated in detail in recent decades. Some particularly enthusiastic advocates even claimed that chaos theory reduced the traditional predictable linear mathematical models of physical systems to myths, but that was going much too far: the linear systems were always known to be approximations to reality, and they generally proved good enough approximations to get the job done as well as it needed to be. This document uses the simplest, crudest possible mathematical models and gets a fair amount of mileage out of them.
On the other side of the coin, critics suggested that it was really the simple models that did all the useful work, and so chaos theory was mostly big talk that was of little practical use. However, if it wasn't the "new science" people claimed it was, it is still a valid element of systems theory and has its applications.
Once again, an understanding of nonlinear and chaotic systems is not in itself all that useful in a simple physics document. The issue is simply to warn against complacency: the real Universe is not always so simple. It was possible for Laplace to state that, given a knowledge of initial conditions and the rules of mechanics, the behavior of the Universe could be predicted indefinitely into the future, but nobody believes that now. Modern science has shown there is a fundamental uncertainty in physical measurements, below which it is literally impossible to obtain any more detail, and given nonlinear systems such undetectable variations may grow, in time, to a cosmic scale. Again, science isn't necessarily an exact science.
BACK_TO_TOP* Science-fiction writer Larry Niven wrote a pair of novels titled THE INTEGRAL TREES (1984) and THE SMOKE RING (1987) that have some interesting insights into orbital mechanics. These two novels postulated a double star system, consisting of a small white dwarf star named "Voy" in orbit around a bright central star named "T3".
Voy had a giant planet named "Gold" in orbit around it in turn. Voy had once been a bigger, brighter star itself, but the stellar explosion that turned it into a hot stellar cinder stripped Gold of its gaseous outer layers, resulting in a ring or "torus" of gas that stretched completely around Voy in the planet's orbit. This "Smoke Ring" was long-lasting and contained enough debris to support the evolution and propagation of life. Plants evolved that produced oxygen, eventually making the Smoke Ring an environment where humans could breathe and survive. When a mutiny stranded an interstellar expedition from Earth there, successive generations of humans colonized the Smoke Ring and gradually spread all the way around it.
The major landmarks in the Smoke Ring were the "Integral Trees", which were huge free-floating trees about a hundred kilometers long that were curved into an elongated "S" shape, similar to the integral symbol used in calculus. Humans tribes colonized the tips of the Integral Trees, which were covered with jungle-like "tufts" of greenery, while the intermediate parts of the tree were generally barren.
The orbit of an object is defined at its center of mass, which was at the center of an Integral Tree. Since the Integral Tree was an elongated object, tidal forces from the white dwarf star forced the Integral Tree to point toward Voy at the center of its orbit, crossways to the tree's motion. Incidentally, this is known as "gravity gradient stabilization", and small satellites have been built with a mass on an extension to ensure that they always point straight down to the surface of the Earth as they orbit around it.
In any case, an independent object orbiting below or "in" -- inward to the center of the orbit around Voy -- of the center of mass of the Integral Tree would have a faster orbit than the tree, while an independent object orbiting above, or "out" -- outward relative to the orbit of the tree around Voy -- of the center of mass of the Tree would have a slower orbit. However, since the Integral Tree was a solid object, the entire Tree orbited at the same speed. This meant that the inner tuft of the Tree was moving slower than independent objects in the same orbital radius, and the outer tuft of the Tree was similarly moving faster than independent objects in the same orbital radius.
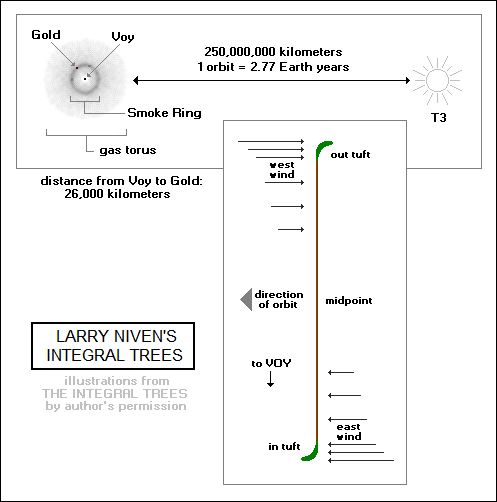
At the inner tuft, since the gases in the Smoke Ring were moving at their natural orbital speed but the tuft of the tree was moving more slowly, the tuft was in a perpetual howling wind blowing from behind the Tree's direction of motion. The inner tuft of the Tree curved in the direction of its motion to offer less resistance to this wind, while the tuft filtered debris from the wind to support the growth of the Tree. Gravity was no longer completely balanced by centripetal acceleration, and the result was that the humans felt a net gravitational force that grew stronger the farther "in" they went. Of course, they had to stay on the inside of the curve of the tuft, since if they went below they could fall down into the Smoke Ring.
In a complementary fashion, the outer tuft was moving faster than the gases at its orbital radius, and so the outer tuft faced a similar howling wind but in the opposite direction, coming from in front of the Tree. As with the inner tuft, it curved away from the wind and the tuft collected debris blown into it. Centripetal acceleration was no longer balanced by gravity, and so the humans felt a net "artificial gravity" that grew stronger the farther "out" on the tuft they went. Once again, they had to stay on the inside of the curve, or they would be flung up into the Smoke Ring by their excess velocity.
The excess gravitational pull on the inner tuft of course had to be balanced by the excess centripetal acceleration on the outer tuft, or the Integral Tree would not have been in a stable orbit. This set up a force between the two ends of the Tree that increased as the Tree grew longer, and so limited its length. In fact, old or diseased Trees could snap apart at the middle, with disastrous consequences for the human colonies in the tufts. By the way, Smoke Ring materials unsurprisingly tended to accumulate in the L4 and L5 libration points defined by Voy and Gold, and these locations amount to "metropolitan areas" in the Smoke Ring.
The idea of making movies out of THE INTEGRAL TREES and THE SMOKE RING is appealing, though the special effects would be so difficult that an animated film might be the best approach, particularly since the human colonists had evolved into very tall and gangly forms in the low gravity and could not be played by any normal human actor. Unfortunately, the environment of the Smoke Ring is so alien and disorienting that most viewers would not be able to figure out what was going on, and it seems plausible that if shown on the wide screen, it might cause vertigo and motion sickness.
* Related concepts of orbital mechanics are embodied in some schemes for space tether systems. Tethers have already been described in an earlier chapter for setting up artificial gravity, but they have other potential applications. Imagine a space station in orbit around the Earth that has a tether hanging downward with the end not far above the Earth's atmosphere, and a second tether hanging upward from the station, with the end in a higher orbit.
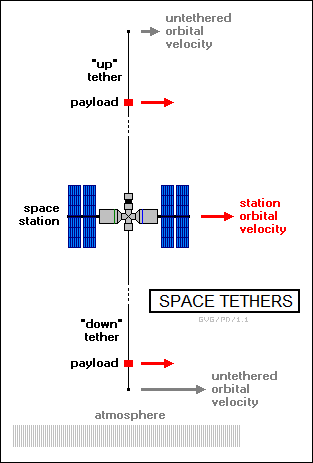
Suppose the station crew wants to send a payload back down to Earth. The current way of doing this is to use retrorockets to kill the payload's orbital velocity, causing its orbit to decay. Using a space tether, all that has to be done is winch the payload down the "down" tether. If the payload were free to orbit on its own it would speed up as it descended, but since it's linked to the station with the tether, it can't. Once it reaches the bottom of the tether it is released and, lacking the velocity to stay in orbit, re-enters the Earth's atmosphere.
Since the station slows down the payload as it is winched down the tether, the payload similarly makes the station speed up -- the tether connection is two-way, after all. That means that not only is the payload returned to Earth more cheaply than if retrorockets were used, but the station gets a "free" orbital reboost out of the transaction.
Similarly, to send a payload to a higher orbit, the station crew can winch it out along the "up" tether. If the payload were free to orbit on its own, it would slow down, but it is dragged along with the station in its orbit. When the payload reaches the end of the tether, it is released and sails off outward into space. Once again, the tether works both ways: the payload slows down the station a bit, and when the payload is released the station falls to a lower orbit.
Of course, the "down" tether can be used to winch up payloads from low orbit, at the expense of lowering the station's orbit, and the "up" tether can be used to winch down payloads from high orbit, raising the station's orbit. This leads naturally to a more elaborate concept, the spinning tether or "rotavator". Much like before, tethers are hung from the two sides of a central "hub", but in this case the hub is spinning and the ends of the tethers are going in great circles, falling towards Earth and then arcing upward into space again. The idea is that a rocket-boosted aircraft carrying a payload on its back might skip momentarily above the atmosphere, with the maneuver precisely timed so the rotavator sweeps down and snags the payload off the aircraft's back. The rotavator then curves around 180 degrees to release the payload into a high orbit. Another rotavator orbiting above the first might then snag the payload again from its new orbit and release it into a still higher orbit -- and so on.
Rotavators could also be used to snag payloads from higher orbits and pull them down to lower orbits. Since a rotavator loses a bit of orbital altitude with each payload sent upward and gains a bit with each payload sent downward, the rotavator scheme implies that the mass of traffic going up must be more or less matched by the mass going down.
There are other interesting things that can be done with space tethers, but they are beyond the scope of this document. So far, only small-scale space tether experiments have been performed, and the technology has yet to be put into practical application.
BACK_TO_TOP