
* This chapter follows up the discussion of Newton's laws in the previous chapter by discussing drag and friction; demonstrating some simple practical machines; and then providing a general view of forces and fields in the Universe.
* The examples used so far in this document have generally ignored friction, which makes the math much simpler, but in the real world friction can't be ignored. The friction of an object falling through the air, its drag, is not significant for a compact object falling a short distance, but otherwise that drag ultimately limits how fast the object falls to a more or less fixed "terminal velocity".
The actual terminal velocity depends on the shape and smoothness of the object. A streamlined object has less drag than a blunt one, and a smooth, polished surface has less drag than a rough one. This is because the air consists of a mix of various kinds of molecules. On the average, except for the occasional breeze or wind, these molecules are not moving at any appreciable velocity. When a moving object hits the molecules in its path, it transfers momentum to them that causes them to bounce away.
Suppose a cylinder is shot out of a cannon, end first. When the flat end surface collides with the molecules, they bounce away in the direction of the cylinder's motion, resulting in a maximum change in their momentum. Since force is the change in momentum, this means a maximum force to slow down the cylinder. This also implies that the force slowing down the cylinder is proportional to its frontal cross-sectional area, since that increases the number of molecular collisions. A long slender cylinder fired out of a cannon has less drag than a short fat cylinder of the same mass.
Now suppose the cylinder is machined to look like a dart with a sharp point and tapered sides. As it flies through the molecules, the tapered sides tend to cause the molecules to bounce off to the sides. Relatively little momentum is transferred in the forward direction to the molecules, while the momentum transferred into the cylinder by the sideways motion of the molecules is, on the average, the same on all sides and balances out. The result is that the dart has much less drag than the cylinder. A rough surface similarly has faces at a microscopic level that can cause the molecules to bounce forward; smoothing and polishing the surface of the dart reduces these losses. There are actually a number of other, subtler considerations in designing an object to reduce drag -- early torpedoes were spindle-shaped, but it was eventually found that a round-nosed cylinder worked better -- but they are well beyond the scope of this document.
These same principles apply to falling objects. Of course, a parachute is an application of such principles; an open parachute has much more drag and a much lower terminal velocity than the parachute in its pack, since the open parachute has much more cross-sectional area to its line of motion for the same weight.
No matter how smooth or streamlined an object is, drag forces increase with speed. Since momentum is directly proportional to velocity, it might seem that drag forces increase linearly with speed, but that's only true for small objects moving at low speed; due to a complicated set of other effects, such as compression of and turbulence in the medium, the drag forces for small objects at high speed or large objects at almost any speed roughly increase with the square of the velocity. In any case, at some speed, the force of drag matches the force of gravity. There is no longer a net force on the object, and the object will not accelerate to a higher speed. It has reached its terminal velocity.
Of course, this does not apply to objects falling in a vacuum. This needs to be emphasized because we live at the bottom of an atmosphere, and it sets our preconceptions on how things fall. If the Earth had no atmosphere, a gram of feathers would fall at the same rate as a gram of steel. That's not too hard to swallow, but a gram of feathers would also fall at the same rate as a tonne of feathers, or a tonne of steel. In fact, everything would fall to earth at the same rate, increasing in speed by 9.81 meters per second every second until impact, no matter how heavy it was or what its shape was. Gravitational force depends on the product of the masses of two objects involved: double the mass of one object, it doubles the force, but by Newton's second law F = M * A, the doubled mass means that twice the force gives the same acceleration. Heavy objects do not fall faster than light ones in a vacuum.
It is drag that makes this simple fact somewhat counterintuitive. A feather is like a parachute, having a large cross-sectional area relative to its weight; if feathers were crushed together into a mass, of course they would fall much faster. The issue of drag did much to confuse scientists for millennia. It was Galileo who managed to cut through the confusion; his decisive work on the subject involved rolling heavy and light balls down ramps, where the rate of fall was slow enough to allow him to accurately measure the time it took for each ball to reach bottom with the crude instruments he had available to him. The story of his dropping two balls off the soon-to-be-leaning Tower of Pisa is generally regarded as a myth.
It should be noted here that one of the other laws of unrealistic cartoon physics is that, if Wile E. Coyote falls off a cliff alongside, say, an anvil, the anvil will somehow move to a position directly above him before impact. (Specialists in cartoon physics summarize this principle as: "Everything falls faster than an anvil.") In the real world nature is indifferent, sometimes to the point of seeming perverse -- a notion described in the well-known principle of "Murphy's Law", or "everything that can go wrong, will" -- but never deliberately sadistic.
* Similarly, if Bob tries to push along an object sitting on the ground, he has to deal with a force of friction proportional to the object's weight and to the roughness between the two surfaces. Interestingly, though it's obvious from experience once pointed out, the force of friction is greater to get a motionless object to move than to keep it moving. The friction force that resists putting an object in motion is known as "static friction", and the lesser friction force that resists keeping an object in motion is known as "sliding friction" or "kinetic friction".
Of course, the friction force can be reduced by making the sliding surfaces smoother and by using a lubricant. Using rollers or a dolly also greatly reduces the force of friction in moving the object, though there are still smaller "rolling friction" forces at work. One of the best ways to overcome friction is to support an object on a blanket of blown air, though this requires a certain amount of relatively complicated technology and a power source.
BACK_TO_TOP* We now know enough to consider the operation of simple machines, such as levers, ramps, gears, pulleys, screw jacks, and so on. An understanding of these devices is based on elementary concepts of force, work, and power.
A lever is one of the simplest tools. Suppose Bob wants to lift a weight or "load" using a long stout stick as a lever. He props the stick on top of a rock for support so that three-quarters of the stick is on his side of the rock, while the other quarter is on the other side of the rock and wedged under the load. The rock is said to act as a "fulcrum", by the way. If he pulls down on the lever, his end of the stick moves three times as far down as the other end of the stick under the load moves up. The total work done on both ends of the stick is the same, but since Bob's end of the stick moves three times farther, he only ends up applying a third of the force. This means Bob has a "mechanical advantage (MA)" of three to one, or in more formal terms:
_________________________________________________________________________ force1 * displacement1 = force2 * displacement2 _________________________________________________________________________
To balance a lever, the product of the mass and length of the lever on one side of the fulcrum must equal the product of the mass and length of the lever on the other side of the fulcrum:
mass1 * length1 = mass2 * length2
In this example, if the lever is a meter long and the fulcrum is 25 centimeters from one end, then 1 kilogram at the long end of the fulcrum balances 3 kilograms at the short end. If the fulcrum is 20 centimeters from one end, then 1 kilogram will balance 4 kilograms. Similar issues of balance comes up in other domains of physics.
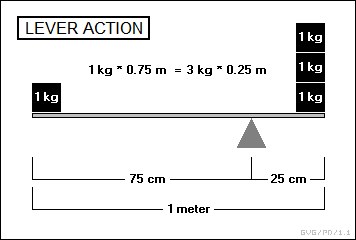
The example above involves arranging a lever to use a small force over a long distance to exert a big force over a short distance. Such a lever configuration can be reversed, using a big force over a short distance to exert a small force over a long distance; this might seem pointless at first sight, but it is useful in building a catapult.
The catapult from Medieval days known as a "trebuchet" (properly pronounced "tray-byoo-shay", though sometimes Anglicized to "tray-bucket") consists of a heavy weight connected to the short lever arm and a sling for a stone projectile connected to the long lever arm. When released, the heavy weight moves the short lever arm over an arc, with the long lever arm moving over the same arc but covering a longer distance, meaning the sling moves the payload at a higher velocity. The increase in velocity is the inverse of the mechanical advantage: if the long lever arm is, say, five times longer than the short lever arm, the sling and its payload has five times the velocity of the short lever arm.
* This configuration of lever, incidentally, is known as a "first class" or "first order lever", meaning that the load is on one end, the work is exerted on the other end, and the fulcrum is between the two. There are two other lever configurations. The "second order lever" features the fulcrum on one end, the work on the other end, and the load between the two: it's a good scheme for nutcrackers, manual paper punches, and the hand-driven wall-mounted press I use to crush aluminum cans for recycling.
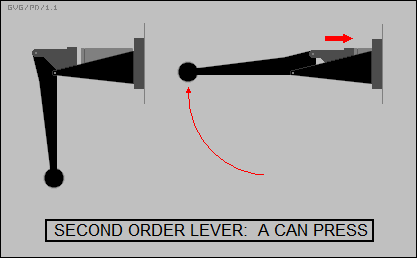
The concept of mechanical advantage applies to the second class lever basically as it does to a first class lever. If Bob has a nutcracker with the jaws clamping down on a walnut a third of the way from the hinge to the grip point, he still gets a mechanical advantage of three to one. However, a "third order lever" -- which features the fulcrum on one end, the load on the other end, and the work exerted in between -- always has a mechanical advantage of less than 1, meaning the force applied to the load is always less than the force exerted on the lever.

In reality, a third order lever is not used to obtain a mechanical advantage as such. It is used to extend reach, for example in ice or sugar cube or salad tongs. It can also be used as a type of catapult mechanism: if a force is applied near the base of a pivoting arm, the tip of the arm will move over a longer path in the same amount of time, allowing it to throw off a load at high velocity.
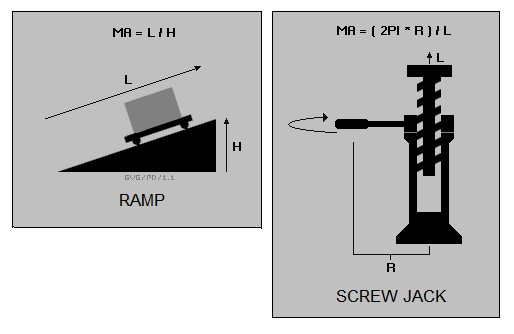
* A ramp is another simple machine. Suppose Bob wants to lift a load one meter into the back of a truck. Lifting it straight up is a good way to hurt himself, so he finds a stout plank three meters long and rolls the load up the plank on a dolly. Once more he only does a third of the work for three times the distance, and has a mechanical advantage of three to one.
A screw jack is simply a ramp wrapped around an axle, with the axle rotated by a handle used as a lever. If the circular motion of the handle is 30 centimeters per revolution, for example, and one turn of the screw lifts a weight by one centimeter, then the mechanical advantage is 30 to 1. My little car has a scissors-type screw jack, in which rotating the handle turns a horizontal screw that raises a mechanical scissors arrangement. Obviously a detailed analysis of this device is a little more complicated, but a simple "input-output" analysis shows that if one rotation of the handle travels 30 centimeters to raise the jack one centimeter, I have a mechanical advantage of 30 to 1.
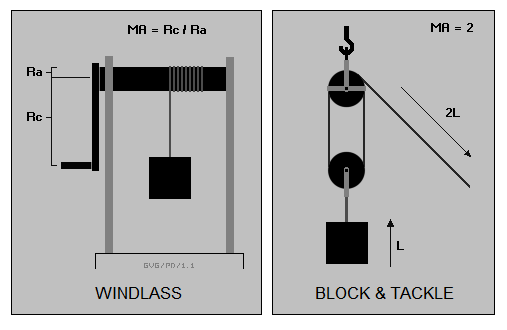
There are other ways to obtain "leverage". For example, a windlass consists of a crank with a radius Rc turning an axle with a radius Ra to wind up a rope. One turn of the crank means one turn of the axle, and so the mechanical advantage is Rc / Ra.
A simple pulley doesn't provide any mechanical advantage, it merely allows a force to be applied in a more convenient direction. For example, a rope slung over a pulley might be tied to the hitch of a car, with the car then driving forward to lift a weight off the ground. A block and tackle involves a pair of pulleys looped together. Pulling on the rope out of one end of the loop makes the loop shorter, but as the loop has two sides, it gets shorter at only half the rate the rope is pulled out of the loop. This means a mechanical advantage of two to one. If Bob makes a block and tackle with two loops, he gets a mechanical advantage of four to one; if he makes it with three loops, he gets an MA of six to one.
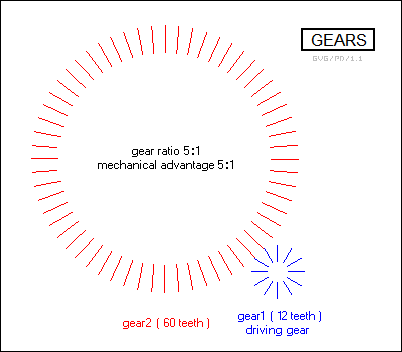
Gears are probably the best-known of all simple machines. Two gears meshing together are basically just a set of wheels moving against each other, with the teeth ensuring they don't slip. If the driving gear is only a fifth as big in diameter as the gear it is driving, then the driving gear performs five rotations for every rotation of the driven gear; it has a "gear ratio" of 5:1. This also means an MA of 5:1.
A classic manual or "stick" automotive transmission is no more than a box full of gears of different ratios. For cruising on level ground, a high gear ratio is used, providing high rolling speed with a minimum of power. For climbing up a hill, a low gear ratio is used, providing low rolling speed with a maximum of power. Of course the transmission has a gear scheme that allows putting the wheels in reverse. The transmission is linked to the engine through a spring-loaded friction plate or "clutch". If Bob is wants to change the gear ratio, he steps on a clutch pedal to release the clutch plate from the engine driveshaft, which temporarily "unloads" the transmission. He then changes the gear ratio with the stick and releases the clutch pedal, loading the transmission again.
* Traditionally, manual transmissions have four to six gear ratios. Now many cars have a "continuously variable transmission (CVT)" that can vary continuously from its lowest gear ratio to its highest gear ratio. Actually, calling it a "gear ratio" is somewhat misleading, since a CVT doesn't have gears as such.
To get the basic idea of a CVT, imagine a small car with a transverse (sideways) mounted engine and front-wheel drive. There's a disk on the engine shaft and a disk on the front-wheel driveshaft, with the two disks linked only by a belt. Obviously, if there's a disk with a small diameter on the engine shaft and a disk with a big diameter on the driveshaft, the gear ratio is low, good for climbing hills; if the engine shaft disk is big and the driveshaft disk small, then the gear ratio is high, good for economical fast cruise.
The magic trick in a CVT is to make the two disks effectively change diameter. This is done by actually making each in the form of two disks, in the shape of shallow cones with the tips together, one of the cones being fixed to the shaft and the other able to be moved up and down the shaft using an actuator system. Pulling the two cones apart makes the belt ride lower in the space between the cones, reducing the diameter over which the belt is driven, while drawing the cones together makes the belt ride higher, increasing the diameter.
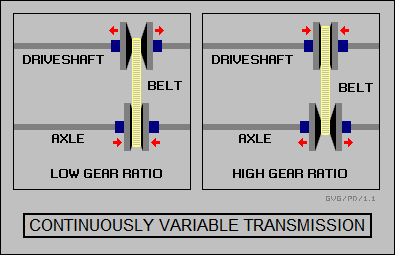
Of course, the two sets of cones have to be adjusted in step, one set closing and the other opening, to ensure that the belt doesn't go slack. The idea that a belt can be manufactured that will put up with this sort of workout is hard to believe; it consists of dual sets of steel bands, held in place with a string of strong metal cross members.
The only shift settings necessary for a CVT are reverse, park, and forward. The basic concept of the CVT is not new, going back to the Renaissance polymath Leonardo da Vinci (1452:1519) at least. The first practical CVT design was patented by Dutch inventors Hub and Wim van Dorn in 1958, and the first full production cars with CVTs appeared in the late 1980s.
The CVT is a clever idea, but it is now being confronted by advanced transmissions featuring as many as ten gear ratios. Manually shifting such a transmission would be a nuisance, but digital electronic control systems are used to automate and optimize the process. In fact, since the automatic control system shifts far more capably than any human driver, the transmission can be made lighter since it operates under less stressful conditions. Digital electronic transmissions are likely to become universal in not too long a time.
BACK_TO_TOP* We have defined force, and discussed gravitational forces a little. Gravity is actually only one of four fundamental forces in the Universe:
All other forces are just indirect manifestations of these four basic forces. The only ones we actually deal with directly are the gravitational and electromagnetic forces. The strong nuclear force holds the cores of atoms together, while the weak force only shows up in certain processes of atomic disintegration, and in fact it seems so unlike the other three forces that physicists tend to call it the "weak interaction" instead. The strong and weak nuclear forces were completely unknown to classical physicists and will not be mentioned further in this document.
The gravitational force is the most familiar of these four forces, since we deal with it all the time. Gravity is the weakest of all the four forces, and is about forty orders of magnitude (one followed by 40 zeroes) times weaker than the electromagnetic force. To visualize just how weak a force gravity is, consider that when Bob picks up a brick, he is overcoming the gravitational attraction of the entire Earth on that brick. However, gravity is the only one that is effective over long distances, and so predominates over the entire Universe.
Gravity is an attractive force between two or more masses, such as the Earth and the Moon. It's not actually restricted to such large masses, since the attraction exists between any two masses of any size, but since gravity is so weak it's hard to notice in smaller masses. As Newton discovered, the size of this force is proportional to the size of the two masses, and inversely proportional to the square of the distance between them:
_________________________________________________________________________ gravitational_force = constant * mass1 * mass2 / distance^2 _________________________________________________________________________
-- where the constant has a value of 6.672E-11 in standard metric units, and the distance is measured between the centers of the individual masses. Double the size of one of the masses, and the force is multiplied by two. A big planet like Jupiter has much stronger gravity than does the Earth, 2.54 times greater to be specific. Double the distance, the force is divided by four. If Bob blasts off from Earth in a rocket, the farther he goes, the more the force falls off.

Bob flies around the solar system to other planets all the time, experiencing different gravitational forces and having a different weight on each planet. Since the vast majority of us never get very far off the ground, much less travel to other planets, in our practical experience the force of gravity is a constant, with an acceleration of 9.81 meters per second, as discussed earlier.
It should be noted that Newton never really claimed he understood why gravity behaved as it did, famously stating: "I frame no hypotheses." He accepted it as simply as a given, a fundamental rule of the way the Universe worked, and though modern physics has taken the idea somewhat farther, this document accepts it as a fundamental rule as well.
* Physicists use the concept of a "field" to describe forces like gravity. This can be considered as a three-dimensional map of the direction and magnitude of the force at any point in space. The idea was originally conceived by the brilliant English researcher Michael Faraday (1791:1867).
Two-dimensional representations of fields usually use lines to map such fields, with the density of the lines giving the strength of the field and arrows attached to the lines to give their directions. Leveraging off this abstraction, physicists often refer to "lines of force" or "lines of flux" in descriptions of fields and field interactions, though in classical physics the fields are actually continuous and the lines are just a convenient fiction, much like the altitude lines around mountains and other geographical features on relief maps.
The density of the lines of force gives the strength of the field and the amount of force it produces. In the special case of living on the surface of the Earth, the gravitational field is effectively uniform. No matter where we place a mass in the three dimensions of our immediate surroundings, the direction of the force is straight down and the magnitude is effectively the same. Potential energy in this uniform field, as mentioned in the previous section, is directly proportional to the height of a mass. If the mass is raised any significant fraction of the Earth's diameter, the gravitational force falls off and calculating potential energy is trickier.
Every object in the Universe exerts a force on every other object in the Universe. However, in most analyses of gravitational forces in the greater Universe, the gravitational field is regarded as acting between simple points of matter that have no extent. This is actually a very good approximation for nearly all practical purposes.
Visualizing this from a field perspective also helps explain why gravity obeys an "inverse square" law, decreasing in strength with the square of the distance. The gravitational force of the Earth can be visualized as lines of force radiating with uniform density in all directions, with the direction of the lines pointing into the Earth.
Now let's draw an invisible shell around the Earth at some radius. All the lines of force pass through this shell. Since the surface area of a sphere is 4 * PI * radius^2, then if we draw a second shell at double the radius, the surface area of this shell is four times that of the first. The same number of lines of flux pass through this outer shell as they do the inner shell, but the surface area has been squared, meaning the density and so the strength of the gravitational field has been attenuated by the same factor.
* Electromagnetic forces have similarities to and differences from gravitational forces. Gravitational forces occur between masses. Mass is irrelevant to electrical forces, they only rely on a property known as the "electrical charge" of the objects involved.
"Charge" is another fundamental concept, one that can only be explained in terms of itself: an electric field works on charges, charges are what an electrical field works on. However, charges are tangible, and can be measured. Physics defines a certain fundamental unit of charge that cannot be subdivided further. This charge is very small and is usually measured in terms of 6.24E18 of these basic charges; this amount is known as a "coulomb". Charges can flow from one object to another, with a rate of flow of one coulomb per second given as an "ampere".
The basic law of electrical force is very similar to that of gravity. The electrical force is proportional to the product of the charges of each object and inversely proportional to the square of the distance between them:
_________________________________________________________________________ electrical_force = constant * charge1 * charge2 / distance^2 _________________________________________________________________________
-- where the constant has a value of 8.9875E9 in standard metric units. A charged object in an electric field will move in the direction of the lines of force. This relationship was discovered by the pioneering French electrical researcher Charles Augustin de Coulomb (1736:1806) -- the coulomb of charge is of course named in his honor -- and the electrical force is sometimes called the "Coulomb force" in his honor. Bob can easily demonstrate this force by rubbing a balloon on his hair, a process that strips off charges; the balloon will then stick to walls or the ceiling. The same effect makes styrofoam packing peanuts difficult to handle, since they tend to stick to the fingers.
There are two types of charges, positive and negative, with objects with like charges repelling each other and objects with unlike charges attracting each other. By the way, the acceleration of an object due to an electric force on it is still proportional to its mass. The amount of charge on the object may change the amount of force on it, but given a specific force the acceleration is strictly due to the mass.
The alert reader will notice that the definition above is for "electrical force" even though the topic under discussion is "electromagnetic forces". The electric force is straightforward: put a charged object in an electric field, it will be accelerated towards a concentration of opposite charges or away from a concentration of like charges. The magnetic field is harder to grasp.
If we have a permanent magnet in the shape of a ring with a gap cut out of it, there will be a magnetic field between the "magnetic poles" on either side of the gap. If we throw a charged object through the gap, it will not be accelerated towards the poles; it will instead be pushed out one side or other of the gap. In more general terms, if a charged object flies across the lines of force of a magnetic field, the object is pushed sideways relative to its direction of motion, with a force proportional to the amount of charge on the object, the intensity of the magnetic field, and the velocity of the object.
It was recognized early on by researchers playing with electricity and magnetism that the two were related: a current passed through a wire will generate a magnetic field around it that can, for example, turn a compass needle. In an inverse fashion, passing a wire through the gap in a magnet would generate an electrical current. Further details of magnetism are a bit beyond the scope of this document and will need to be discussed elsewhere; however, it can be said without more explanation that magnetism is not a distinct force, actually being just a subtle manifestation of the same electrical force. In general, an electric field is produced by an accumulation of charges, while a magnetic field is produced by moving charges. Why this was so couldn't be explained by classical physics, it was just accepted as "the rules".
Incidentally, Michael Faraday arrived at the concept of a field through the classic experiment of placing a magnet under a sheet of flat sheet of paper and then sprinkling iron filings on the paper; the filings then oriented themselves along the magnetic field, allowing it to be visualized. It was a major step forward in the comprehension of the mysterious "action at a distance" of gravity and electromagnetism, though it really didn't say much about the underlying causes of either phenomenon. Faraday lacked a formal education, having lifted himself up from dire poverty at great effort, but he had one of the most well-developed senses of physical intuition in the history of the science.
* As mentioned, electromagnetic forces are vastly more powerful than gravitational forces. If Bob picks up two bricks and holds them out in parallel in front of him, he will not be able to sense any gravitational force between them, and in fact he wouldn't be able to sense a force with anything less than the most exacting experimental apparatus. If he picks up two magnets, each the size of a brick, and holds them in front of him, they will slam together and he won't have the strength to pull them apart.
Both electromagnetism and gravity are long-range forces, and so it seems odd that gravity, which is so vastly weaker than electromagnetism, is the predominant force in the Universe at large scales. There is a major difference between electromagnetism and gravity, however: as mentioned, electrical charges have "polarity" -- they can be positive or negative, with a repulsive force for like charges and an attractive force for unlike charges. In contrast, gravity is, as far as anyone has ever seen, always attractive.
The strength of the electromagnetic force also limits its long-range effects. It is so strong that it tends to pull charges from one object to another. If Bob scuffs his feet on a carpet to get a charge imbalance and then touches Alice, charges jump between the two in a spark, correct the imbalance, and Alice says: "Ouch!". Similarly, if on a larger scale, on a hot day rising air masses in thunderhead clouds will create a charge imbalance that will be corrected with a lightning bolt. Charge imbalances tend to be self-correcting, and overall the Universe remains electrically neutral.
Since gravity operates on a cosmic scale, the fact that it is very weak is highly significant: if it were substantially stronger, the entire Universe would collapse in on itself, and that would be the end of that. However, it must be emphasized that, except for gravity, the forces we see in our daily lives -- from our own physical work, the operation of a car or similar machine -- are derived from the electrical force, if sometimes very indirectly.
It should be noted that in recent years hints have arisen that there may be some sort of repulsive gravitational force. It was learned in the 20th century that the Universe is expanding, having been born in a highly dense and energetic state in a "Big Bang" billions of years ago, then expanding and cooling off to form planets, stars, and galaxies. The discovery that the Universe seems to be expanding at a faster and faster rate has suggested the existence of a mysterious "dark energy" that produces a negative gravity effect. However, nobody's really sure what dark energy is or even that it actually exists, and it's far beyond the scope of this document anyway.
* As a footnote to fields, inventors of perpetual-motion machines and the like seem to have an odd attraction to fields. They particularly like to play with magnets. It doesn't take much inspection to show that fields violate neither energy conservation nor Newton's laws of motion.
As far as energy conservation goes, an object in a field can acquire no more energy than is put into it by work. The simplest example is raising a mass in a constant gravitation field. As described in the previous chapter, on Earth this requires an amount of work given by:
9.81 * height
-- which is of course the potential energy acquired by the mass. The same reasoning applies to electric and magnetic fields, the only main difference being that it is much easier to manipulate or create these fields, for example by moving permanent magnets around or generating a magnetic field with a current. Moving the magnets and producing a current requires work, however, and there's no way to get more work out of any such arrangement than is put into it.
As far as Newton's laws go -- if Bob drops an object on Earth, it is technically not as much true that it falls to the ground so much that the object and the Earth fall towards each other, each having the same but opposite momentum in the interaction. Since the Earth's mass is presumably vastly greater than that of the object, the velocity of the Earth is immeasurably smaller. If it were a case of two planets of equal size, they would fall towards each other, accelerating at the same speed, and meet in the middle. The total momentum of the system at all times in any case is zero.
Another misunderstanding about fields is that their action consumes energy, even in static scenarios. This isn't true: although the Earth's gravity is pulling down on Wile E. Coyote's anvil at all times while it is hanging from a cliff, simply pulling on it doesn't use up any energy. The Coyote had to expend energy to get it to the top of the cliff, and it will release energy when it falls on him, but as long as it remains stationary, not the slightest amount of energy is expended.
Of course, what confuses the matter is that if the Coyote falls off the cliff and grabs on to a branch, he'll expend energy just hanging there. In reality, if a plastic dummy of the Coyote ballasted to have the same weight were tied to the branch, it would stay there indefinitely with no consumption of energy. The Coyote, like any living being, expends energy in biological processes for as long as he is alive and has to expend additional energy to perform any action, such as keeping his fingers wrapped around the tree branch.
From an energetic point of view, the Coyote is something like the kind of inflatable yard displays set up on holidays -- ghosts and giant spiders at Halloween, santas and snowmen at Christmas, monster bunnies at Easter. If they were airtight, they could be inflated and left in place with no additional input of work, but they aren't; their structure must be maintained by the continuous operation (and energy drain) of a small fan. If the energy supply to the fan is cut off, the display collapses, and if the Coyote doesn't have periodic inputs of energy, he collapses as well.
There is something mysterious about fields, and since they seem somewhat magical it is tempting to think that they are more magical than they are. Despite that, from a fundamental physics point of view a gravitational field pulling together two masses is not all that different from, say, a stretched spring pulling together two masses. It's just that with a gravitational field the "spring" is invisible.
BACK_TO_TOP