
* The most fundamental concepts in mechanics were derived by the great English scholar Isaac Newton in the 17th century, in the form of what are now known as Newton's three laws of motion -- three simple principles that describe the motion of objects. This chapter provides an introduction to these laws and demonstrates how they relate to the concepts of "work" and "energy".
* One of the first questions addressed in the development of mechanics was: Why does some object keep moving even after the force applied to it goes away? If a cannonball is blasted out of the mouth of a cannon, it flies through the air in a smooth curve until it strikes something or is pulled down to the ground by gravity. The answer to this question was finally unraveled by the Italian scientist Galileo Galilei (1564:1642). Galileo saw through the question by seeing that the concept of motion was strictly relative: it is arbitrary to say that A is in motion relative to B, or the reverse.
That sounds like a deep and exotic concept, but that's reading too much into it. Suppose Bob's on a ship, inside a closed cabin, sailing on a glassy smooth sea. If he doesn't look outside, there is no way for him to know if he is moving or not. The physics of everything in the room would be exactly the same while the ship was in uniform motion as it would if the ship was sitting at the dock. This can be broadly referred to as the "relativistic equivalence principle".
The idea that there was an absolute state of rest was a natural mistake, since we live on a large ball of rock called the Earth that is a lot bigger than we are, bigger than anything that we can set into motion. This means that the Earth seems very convincingly at rest, and anything that moves relative to it seems very convincingly in motion. It is much easier to see the relativity of motion by imagining Bob floating in space inside a glass box. He sees his sister Alice, who likes to help Bob perform experiments, flying past him in a glass box of her own. As far as Bob is concerned, it is Alice who is in motion. However, from the point of view of Alice in her glass box, it is she who is motionless and it is Bob who is moving, in the opposite direction. Bob and Alice reside in what are referred to as different "inertial frames of reference".
Modern generations have realized that the Earth is itself in motion around the Sun, and the Sun is in motion around the center of our Galaxy. Such cosmic concepts of motion are still hard to grasp intuitively, and so in practice we invariably think of something sitting motionless on the ground as being "at rest" while a car driving over the ground is "in motion". The Earth defines a "local" frame of reference for our motions, and it would be silly to think otherwise. It is useful for those interested in mechanics to keep in the back of their minds that our Earth-centered viewpoint is a parochial point of view, and in other inertial frames of reference, it is the Earth that is in motion.
* Galileo's consideration of the meaning of rest and the meaning of motion sounds a little like doubletalk, but it did have practical implications. The main implication was that motion itself was less significant than changes in motion, or accelerations. A force causes a change in motion of an object, and once set into motion that object will remain on that path of motion, until another force speeds it up, slows it down, changes its direction, or causes any other change in its motion.
Galileo laid the groundwork, but never managed to link all the ideas together; that task was performed after him by the English genius Sir Isaac Newton (1642:1727) in his three laws of motion, outlined in his revolutionary treatise PRINCIPIA MATHEMATICA, published in 1687:
These three simple, elegant laws are adequate to describe the motion of all objects in the Universe.
BACK_TO_TOP* The First Law observes that objects in motion tend to remain in motion in a straight line. The magnitude of this tendency is given by a property called "momentum", which is unsurprisingly related to the bulk or "mass" of an object, and the velocity with which it is moving. In mathematical terms, the First Law is expressed as:
_________________________________________________________________________ momentum = mass * velocity. _________________________________________________________________________
In the metric system, mass is by default measured in kilograms. Momentum, like velocity, is a vector, and has a magnitude and a direction.
The Second Law defines force and mass. In mathematical terms, the Second Law is expressed as:
_________________________________________________________________________ force = mass * acceleration _________________________________________________________________________
What is a force? It's what accelerates a mass. What's a mass? It's what is accelerated by a force. Gravity, for example, is a force that accelerates a mass such as a brick. Force and mass are fundamental concepts, basic definitions that have to be taken as givens. In the metric system, force is measured in "newtons".
Since acceleration is, in broad terms, the change or "delta" of velocity over an increment or "delta" of time, and momentum is mass times velocity, with the mass being constant:
force = mass * acceleration
= mass * delta_velocity / delta_time
-- and:
_________________________________________________________________________ force = delta_momentum / delta_time _________________________________________________________________________
This is another way of stating the Second Law, or in other words force is equivalent to the rate of change of momentum over time: the greater the force, the greater the rate of change of momentum.
* Incidentally, mass and weight are not the same thing. A mass remains constant no matter where it is in the Universe. In contrast, weight is just a measure of the force of gravity on a mass. If Bob goes to the Moon, he would only weigh a sixth of what he weighs on Earth, but his mass would be the same.
Modern physics recognizes that the "matter" in the Universe that constitutes its mass is made up of vast numbers of very small particles, known as "atoms", that as an approximate (and not entirely true) rule cannot be subdivided further. There are a roughly a hundred different types of atoms that have different properties. Atoms can combine to form a wide range of "molecules" that have different properties from the atoms that make them up.
Atoms and molecules can be organized as solids, liquids, or gases. While we live on Earth completely surrounded by matter, it is actually relatively scarce in the Universe. Once we travel away from the Earth into space, the amount of matter in a volume of space becomes effectively negligible. Space empty of appreciable amounts of gaseous matter is known as a "vacuum"; most of the Universe is a vacuum.
* Some examples can help demonstrate what the First and Second Laws mean in practice:
* Closely related to the concept of force are the dual concepts of "work" and "energy". Work is defined as the sum of forces applied to a mass over a distance. Energy is the capacity to do work.
The foundations of these concepts were laid in Newton's work, as well as in the work of the German polymath Gottfried Wilhelm Leibniz (1646:1716), a rival of Newton. The notions were more clearly defined by the experiments of the Dutch physicist Willem s'Gravesande (1688:1742), who performed meticulous studies of metal balls on strings bouncing against each other, spherical masses dropped on beds of clay from different heights to see how big of a dent they made, and so on. In the 19th century, the notions of work and energy were investigated in detail by the British physicist James Prescott Joule (1818:1889) and the German physicist Julius Robert von Mayer (1814:1878), leading to the precise formulation of modern concepts of work and energy by another German physicist, Hermann Ludwig Ferdinand von Helmholtz (1821:1894).
For a simple example of work and energy in action, imagine that Bob lifts a mass against the Earth's gravity. In his immediate surroundings, the force of the Earth's gravity is for all practical purposes constant. Actually, gravity grows weaker the farther an object is away from the Earth, but for such short distances the force of gravity varies too little to notice.
Since gravity is exerting a force on the mass, he has to exert a force on the mass to lift it against gravity. If he lifts the mass to, say, three meters, the total work performed on the mass is the force times three meters. At least in terms of pure physics, how long it takes him to lift the mass doesn't matter, nor do any side trips taken on the way up; that all amounts to wasted motion, what is important is that it is lifted three meters.
If the mass is raised to that height, it then has a capability to do work itself by falling back down again. This is the "potential energy" of the mass, and is the same as the amount of work required to raise it that height. The potential energy of a mass being raised near the surface of the Earth is given by:
_________________________________________________________________________ potential_energy = 9.81 * mass * height _________________________________________________________________________
Energy and work are measured in "joules", named after James Prescott Joule. If a mass of ten kilograms is raised three meters, its total potential energy is:
potential_energy = 9.81 * 10 * 3 = 294 joules
The rate at which work is done or energy is expended is defined as "power", which is measured in "watts", or joules per second. If Bob lifts the weight in five seconds, the power used to do it is:
power = 294 / 5 = 58.9 watts
Of course, inversely, multiplying the power used times the time it is applied gives the total energy.
energy = power * time = 5 * 58.9 = 294 joules
This definition leads to an alternate unit for energy named "kilowatt-hours", often used in electrical power distribution. A kilowatt-hour is a thousand watts applied for an hour, or 3,600 seconds, and so is equivalent to 3,600,000 joules.
* Moving objects also store energy due to their motion. A flying brick, for example, has the capability of doing destructive work. This form of energy is known as "kinetic energy".
The kinetic energy is the sum of all the force provided over a distance needed to get the brick to a specific velocity. Consider a simple example, where a mass is accelerated from rest by a constant acceleration for a specific time interval. As shown earlier, for a constant acceleration, the average velocity is half the final velocity V, so the total distance D traveled in the given time T is:
D = ( 1/2 ) * V * T
Now since:
force = mass * acceleration = M * A
-- and since:
energy = force * distance
-- then for this case:
energy = M * A * D
= M * A * ( 1/2 ) * V * T
Since in this case the acceleration is constant, then the acceleration is the final velocity V divided by the time interval T, and so:
energy = M * ( V/T ) * ( 1/2 ) * V * T
= ( 1/2 ) * M * V^2
This gives the definition of kinetic energy as:
_________________________________________________________________________ kinetic_energy = ( 1/2 ) * mass * velocity^2 _________________________________________________________________________
Kinetic energy and momentum have a simple relationship:
_________________________________________________________________________ kinetic_energy = ( momentum^2 ) / ( 2 * mass ) _________________________________________________________________________
-- since:
kinetic_energy = ( ( M * V )^2 ) / ( 2 * M )
= ( M^2 ) * ( V^2 ) / ( 2 * M )
= ( M * V^2 ) / 2
Kinetic energy, and in fact any sort of energy, is a scalar, not a vector, quantity: it has a magnitude, but no direction. While this derivation is only for a constant acceleration, the kinetic energy only depends on the mass and velocity. How the mass got to that velocity doesn't matter, and so the definition is true in the general case as well.
By the way, since momentum is given as mass times velocity, this expression can also be redefined as:
kinetic_energy = ( 1/2 ) * momentum * velocity
* Notice that kinetic energy is proportional to the mass and to the square of the velocity. This means that even a small mass moving very fast has a lot of kinetic energy. Suppose Wile E. Coyote is hit by a 1-tonne (1,000-kilogram) car moving at 100 kilometers per hour (or 100 * 1,000 / 3,600 = 27.8 meters per second). Then the total kinetic energy is:
kinetic_energy = ( 1/2 ) * 1,000 * 27.8^2 = 385,800 joules
Let's consider how fast a 10-gram mass would have to be moving to have this same kinetic energy:
velocity = SQRT( 2 * kinetic_energy / mass )
= SQRT( 2 * 385,800 / 0.01 ) = 8,780 meters per second
= 31,600 KPH
* Energy is a concept now taken so much for granted that it is startling to realize that Isaac Newton didn't have a clear concept of the idea. It was certainly apparent to Newton that a stone sitting on top of a high wall had a capability to do damage to someone standing below if it were knocked off, and of course everyone understood that a flying cannonball could be dangerous -- indeed, that was the point of cannonballs.
Leibniz was the first to articulate the idea, coming up with the terms "vis viva" and "vis mortua", which were direct ancestors of the modern definitions of kinetic and potential energy respectively, but the word "energy" itself wasn't introduced until 1807, when it was suggested by the brilliant British polymath Thomas Young (1773:1829). It would take several more decades to refine the notion into its modern form.
Energy is a highly abstract concept: motion and mass are easily observed, but it's not like anyone can actually see energy, except by implication. From that point of view, it is also surprising to realize that in modern times, energy is something we can actually measure to a high degree of precision.
BACK_TO_TOP* Energy is said to be a "conserved" quantity. Wile E. Coyote exerts work to haul an anvil to the top of a cliff, giving the anvil potential energy, and this potential energy is then converted back into kinetic energy when the anvil falls back down to the bottom of the cliff, with friction effects causing losses along the way.
This basic principle is, as far as anybody has ever seen, absolutely unbreakable: energy is conserved. It cannot be created or destroyed, just converted into different forms. The energy "budget" before a physical event occurs remains exactly the same after the event occurs; only the forms are changed. Helmholtz was the first to articulate this concept in its modern form, though he referred to kinetic energy as "living" energy and potential energy as "tensional" energy.
The law of conservation of energy is why most perpetual motion machines won't work. Typical "classic" perpetual motion machines operate in a cycle, with an output feeding back to an input. The Dutch artist Maurits Escher (1898:1972) was fond of making designs on paper along such lines, such as water flowing in a loop and driving a waterwheel. Escher's work was deliberate and obvious fantasy, playing "crazy house" games with perspective; everybody knows that water doesn't flow back uphill as a normal circumstance. The perpetual motion machines created by crackpots are usually just as absurd, with most of the effort in the exercise focused on trying to conceal the absurdity. No matter how elaborate the disguise, however, the idea that a machine can do useful work indefinitely without input of energy is a dead giveaway. Perpetual motion machines are almost always paper designs, since when they're actually built, they usually don't move at all.

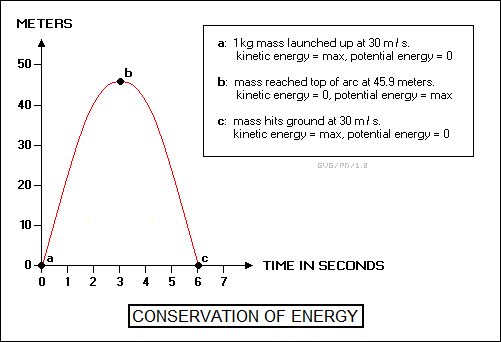
* Back in the real Universe, one simple example of the law of conservation of energy is to catapult a mass into the sky and determine how high it goes. Suppose Bob catapults a 1-kilogram mass upward at an initial velocity of 30 meters per second. Then the initial kinetic energy is:
kinetic_energy = ( 1/2 ) * mass * velocity^2
= ( 1/2 ) * 1 * 30^2
= ( 1/2 ) * 900
= 450 joules
As the mass rises, gravity will slow its rise, converting the kinetic energy into potential energy. Ignoring drag, the mass will stop at the height at which the potential energy equals the initial kinetic energy:
potential_energy = 9.81 * mass * height 450 = 9.81 * 1 * height height = 450 / 9.81 = 45.9 meters
Having reached this height, the mass will then begin to fall back down again. When it reaches the altitude it was launched from, it will once again be moving at 30 meters per second.
Incidentally, an alert reader will realize that the time it takes for the mass to fall back down is given by exactly the same formula used to describe how long it takes an anvil to fall on the Coyote -- it's falling from a stopped position either way:
time = SQRT( 2 * displacement / 9.81 )
= SQRT( 2 * 45.9 / 9.81 )
= 3.06 seconds
Since it takes the mass the same amount of time to fly up as it does to fall back down -- the trip up is exactly the same as the trip down, run in reverse -- the total flight time is 2 * 3.06 = 6.12 seconds.
* Very much the same principles apply to a roller coaster. A classic roller coaster is essentially unpowered, with the cars hauled to the top of a "lift hill" by a chain drive built into the hill, and then allowed to coast freely down the other side over a series of smaller hills, and often (with modern steel-rail roller coasters) through loops and corkscrews. As the cars descend a hill, they pick up speed and kinetic energy; lose it again as they rise to the top of the next hill, acquiring potential energy; pick up speed and kinetic energy once more as they drop down the far side; and so on, with the energy gradually robbed away by friction until the cars finally come to a stop and the passengers stagger out. The initial amount of energy applied to the cars is directly proportional to the height of the lift hill, and in fact the height of the lift hill is the most important single specification for a given roller coaster to an enthusiast.

Another interesting simple example of the law of conservation of energy is the kind of spring-loaded toy gun that shoots little plastic spheres. If Bob pulls back on the trigger of the gun, then up to the limit of the complete compression of the spring, the force he has to exert on the trigger is proportional to the stiffness of the spring and increases directly with the compression of the spring. In mathematical terms:
force = stiffness * compression
In general terms, the stiffer the spring, the harder it is to pull the trigger, and the longer the pull on the trigger, the harder it is to pull further. This relationship is known as "Hooke's law", after the English scientist Robert Hooke (1635:1703), a contemporary of Newton.
Bob does work pulling back on the trigger, with the work being stored up in the spring as potential energy. The work is equal to the force and the distance over which the force is applied. Since the force increases in a nice straight line over the distance of compression, the average force over the entire compression is just half the final compression, so the potential energy is:
potential energy = ( ( 1/2 ) * stiffness * compression ) * compression
= ( 1/2 ) * stiffness * compression^2
When Bob reaches the end of the trigger pull, the spring mechanism is automatically released and the spring returns to its normal length, exerting force on the sphere to accelerate it out of the muzzle, and converting the potential energy into motion, or equivalently kinetic energy. By the way, Hooke's law also applies to stretching a spring, at least up to the limit where it "deforms", or stretches out of shape and won't return to its original form when released.

* As a footnote, Hooke and Newton were bitter rivals. Newton was a brilliant but not always very pleasant person, with a tendency to be resentful of and ungracious to competitors. In a 1676 letter, Newton famously told Hooke: "If I have seen further [than others], it is by standing on the shoulders of giants." This has traditionally been cited as evidence of Newton's modesty, but in fact Hooke was an unusually short person, and in modern times the consensus is that it was more likely that Newton was really being snide, saying that he owed nothing in his own work to a nasty little runt like Hooke.
BACK_TO_TOP* The Third Law describes, among other things, action and reaction. If Bob fires a gun, the bullet flies out the barrel and the gun recoils or kicks back in the opposite direction. Both the bullet and the gun have a certain value of momentum, and in fact it's the same value, though the directions are opposite:
bullet_mass * bullet_velocity = gun_mass * gun_velocity
This means that the velocity of the gun is slower than the velocity of the bullet by the same factor that the mass of the gun is greater than the mass of the bullet. If the gun has 100 times the mass of the bullet, it only moves 1/100th as fast in the opposite direction. In more general terms:
_________________________________________________________________________ mass1 * velocity1 = mass2 * velocity2 _________________________________________________________________________
A more ordinary way to think about the third law is to consider what happens if Bob and Alice are standing on slick ice next to each other, and then push each other away. Bob doesn't just stand still while Alice slides away -- they both slide away from the point they were at. If they're both about the same mass, they slide away in opposite directions at the same speed. If Bob weighs only half as much as Alice, he slides away at twice the speed of Alice.
* The essential point here is that the momentum of a system is a conserved quantity. This is seen in collisions between moving masses, most conveniently visualized as spheres. Such collisions may be "elastic" or "inelastic". In simple discussions of momentum, it is easiest to specify it in terms of one-dimensional movements along a straight line in one direction or the other. We can consider one-dimensional examples of elastic and inelastic collisions.
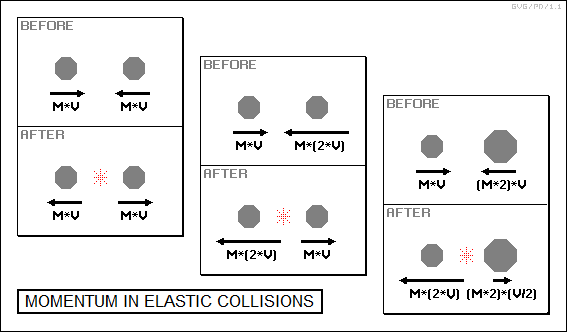
In an elastic collision, the kinetic energy of the masses is preserved. This is the case if the masses are very hard and stiff. In a head-on elastic collision between two spheres of the same size and same velocity in different directions, the two spheres bounce away from each other at their original velocity but with reversed directions. Total momentum is conserved.
If the masses or velocities are not the same in an elastic collision, the results are little more interesting. Suppose one mass is moving twice as fast as a second mass of the same size, and so has twice the momentum. If there is an elastic head-on collision between the two, they bounce away from each other, but the second mass is now moving twice as fast as the first. This occurs because momentum is a vector quantity, and has to be conserved in direction as well as size.
Now suppose there are two masses that are moving at the same speed, but the first mass is twice as big as the second and so has twice as much momentum. If there is an elastic head-on collision between the two, they bounce away from each other, but the conservation of momentum says that the big mass will bounce away at only half its initial speed, while the small mass bounces away at twice its initial speed.
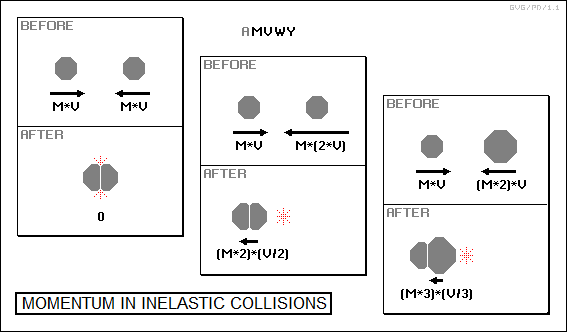
* In an inelastic collision, the kinetic energy of the masses is converted into heat. This happens if the masses are soft and malleable. In a head-on inelastic collision between two spheres of the same mass and same velocity in different directions, the two spheres slap into each other and come to a dead stop. Momentum is conserved once more.
Of course, if the momentum of one mass in such an inelastic collision is greater than the second, its momentum will overwhelm that of the second, and the combined mass that results from the collision will move in the direction of the first. Suppose the first mass is twice the size of the second, but both are moving at the same velocity; then the total momentum of the resulting particle has the same size but opposite direction as the momentum of the second particle. Since the mass of the resulting particle is three times the size of the second particle, the velocity is cut to one-third of the original.
Similarly, if the velocity of the first particle is twice that of the second, the resulting momentum is still the same. However, the resulting particle is twice the mass of the second, so the velocity is only cut in half.
* It is useful to realize that perfectly elastic collisions don't actually occur in the real world: all collisions will have some inelastic component, however small, though in a simple analysis that component may be small enough to be ignored without difficulty. Physics, particularly simple and basic physics, deals with idealized "models" that will not be quite what happens in the imperfect real world, though they may be close enough for practical purposes.
Such simplifications are not done out of any intent to deceive, only out of a desire to make a problem less complicated so it can be easily analyzed. It took pioneering physicists great leaps of intuition to see through the clutter of the real world and extract useful basic principles of physics. It is also useful to realize that sometimes the simplified principles can be wrong or at least misapplied, though all the physics in this document is very simple and thoroughly validated through observation and experiment -- which is always the ultimate test of any theory in the sciences.
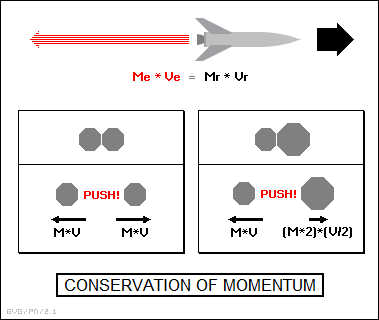
* By the way, the law of reaction is very well illustrated by rocket propulsion. There is a strange popular misconception that a rocket operates by "pushing against the air", but that is not the case. What a rocket does is throw hot gas out the exhaust at high velocity, and by conservation of momentum the rocket moves in the other direction. Essentially, a rocket propels itself using recoil. The air just gets in the way and causes drag.
The more mass in the exhaust and the faster it is sent out, the more thrust it creates and the faster it propels the rocket. In more formal terms, if Me is the mass of the exhaust per second, Ve is the velocity of the exhaust, Mr is the mass of the rocket, and Vr is the velocity of the rocket, then:
Me * Ve = Mr * Vr
Calculating the velocity of a rocket can be tricky since its mass drops as it burns and exhausts fuel, but that is a matter far beyond the scope of an elementary physics document. Incidentally, that's essentially why large rockets have stages: once the first stage has expended its fuel, it's just dead weight and so is discarded, with upper stages expending their fuel and being discarded in turn.
Of course, as mentioned, the Third Law is demonstrated very well by the kick of a rifle or cannon. The recoil increases with the size of the shell being fired -- more mass, increasing momentum -- and the size of the charge firing it -- more velocity, also increasing momentum.
Really powerful rifles can generate quite a kick. Most modern assault weapons use a relatively small cartridge and bullet, reducing recoil, and often have a spring-loaded buffer system in the stock to spread out the time over which the momentum is transferred back to the shooter, making the kick much less abrupt and softer. Such weapons are easier to fire without extensive training, and also much more controllable in full automatic ("machine gun") fire. Similarly, modern artillery pieces often have spring or hydraulic suspensions to soften the recoil, along the lines of the suspensions used in vehicles to soften the effect of bumps in the roadway.
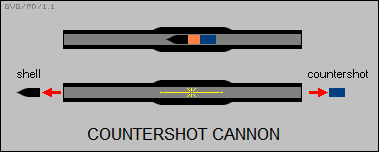
Trying to fit a heavy cannon with shock absorber gear in an aircraft is troublesome. That's why really big guns have rarely been carried on aircraft -- the recoil tends to damage the aircraft. There was some work for a few decades after World War I on a way around the problem, in the form of the "countershot" guns. A countershot gun was a cannon that fired a shell out the front while firing a counterweight out the back. The "countershot" was generally a cardboard cylinder of buckshot packed in grease that could survive being shot out the back of the cannon but would break up quickly, preventing it from being a major threat to anyone or anything behind the aircraft. Nobody ever used such weapons to any extent; they remain something of an historical curiosity.
* As an interesting footnote to the discussion of momentum, here's an extremely devious puzzle. Suppose that we have a fixture consisting of a short pipe standing up on a table. The top of the pipe is fitted with a hub that is free to spin around in the horizontal plane. The hub has an L-shaped hollow tube sticking out each side. An air blower is connected to the pipe below the table; when the blower is turned on, air is forced up through the pipe, through the hub, and out the two tubes, forcing the hub to spin.
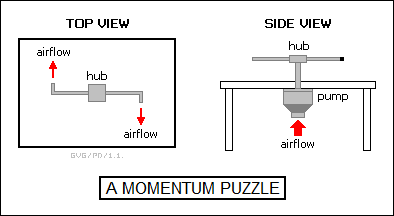
Now suppose that the blower can be put in reverse, so that it draws in air through the fixture instead of blowing it out. What happens to the hub? Does it spin as it did before, or does it spin in reverse?
As it turns out, it doesn't spin at all. The air drawn in from the ends of the tubes is effectively motionless, only acquiring momentum as it travels inward. No momentum is acquired from outside the fixture, and so conservation of momentum means that the hub will remain stationary.
BACK_TO_TOP