
* This chapter provides an introduction to the basic principles and concepts in physics, concluding with a quick review of useful mathematical notation.
* The sciences, according to the brilliant Caltech physicist Richard Feynman (1918:1988), can be defined as an attempt to figure out the rules by which the Universe runs:
BEGIN_QUOTE:
We can imagine this complicated array of moving things which constitute "the world" is something like a great chess game being played by the gods, and we are observers of the game. We do not know what the rules of the game are; all we are allowed to do is watch the playing. Of course, if we watch long enough, we may eventually catch on to a few of the rules. The rules of the game are what we mean by fundamental physics ... if we know the rules, we consider that we "understand" the world.
END_QUOTE
Scientists construct theories of how the rules operate. There is a popular belief that a theory is no more than an arbitrary set of assumptions, but this is demonstrably untrue. One of Gary Larson's FAR SIDE cartoons of the 1990s featured a detective who had gathered the suspects together to determine which was actually guilty of the crime. One of the suspects was a bull elephant in a trenchcoat. The detective announced: "And the murderer was ... THE BUTLER, who gored and trampled the Colonel to death!"
In other words, not all theories are created equal. Feynman pointed out that theories may start out with intuition, a sheer guess, but that guess will have to stand up to critical examination. Given a theory to describe how the rules work, scientists try to observe if they can predict the future course of the game -- or, when possible, set up experiments that demonstrate the validity (or failure) of their theory of the rules. In other words, a valid theory should have "predictive power"; if it doesn't, it amounts at best to merely a useful tool for organization or visualization, and at worst an exercise in empty rhetoric.
The observations and experiments need to provide measurable data, with scientists both in favor of and against a particular theory getting comparable results. Selectively assembling data convenient to a particular theory -- while ignoring or rejecting inconvenient data that can be assumed to be at least as valid -- is regarded as very poor form.
The theory should have, at least as a secondary objective, a certain economy and elegance, containing nothing more than needed to account for observations and being easy to understand or use. This is related to a notion sometimes called "Occam's razor" after the 13th-century English philosopher William of Occam (or Ockham), in which the simpler of two theories that describe the same matter just as adequately is preferred. Concepts of economy, elegance, and simplicity can be somewhat subjective at times, but there are also often objective criteria. One prominent example is the number of unproven assumptions that the theory is based on, the rule of thumb being: "You can only invoke the Tooth Fairy once."
Repeatedly invoking the Tooth Fairy to shore up a theory is also very poor form, the issue being illustrated by the well-known story of the crackpot who claimed that the Earth is flat and rides on the back of a giant turtle. When challenged to say what the turtle was riding on, the crackpot replied: "Hah! You can't trick me! It's turtles all the way down!"
A particular scientific theory is debated by the relevant community of scientists, with the contrarians questioning the assumptions and form of the theory, as well as the validity of the data from observations and experiments that back it up. The advocates defend their position and provide better data. Ultimately, the community comes to a consensus and the theory becomes accepted knowledge. It does, however, remain indefinitely provisional, to be modified, or in the worst case rejected, as new data becomes known.
Scientists generally communicate the results of their work through papers in professional scientific journals. There is a common misconception that anything published in a scientific journal is an established fact, but that is not necessarily the case. The journal simply reports the results of research on a particular subject; the editors can do no more than screen out papers that clearly have no credibility. Once published, other scientists will respond, possibly criticizing the paper, possibly agreeing to it, and responding with research papers of their own.
Like everyone else, scientists range from inept to brilliant, and like everything else they can be influenced by fads and prejudices. Sometimes ideas that fly against the accepted scientific wisdom are quickly accepted; sometimes they are resisted until the data in their favor becomes overwhelming. Scientists still take pride in the fact that when the data does become overwhelming, all but the most stubborn of contrarians generally concede defeat.
The sciences are rooted in fact, but they are still based on an assumption. Scientists observe the behavior of the Universe and devise theories based on inferences from those observations; but there is no way of proving that the Universe will behave in the same way in the future. The sciences are "deterministic", necessarily assuming that the Universe runs by a consistent set of unvarying rules. It may be hard to figure them out, conditions may change over time, but the underlying rules are fixed. This is an assumption, but one validated by all experience, and in fact impossible to refute: if we see what appears to be a violation of the laws of physics, the only constructive thing we can do is assume we have some misunderstanding of our observations or the laws of physics.
The physical theories outlined in this document are recognized as accepted scientific wisdom. This document does focus on classical -- pre-20th century -- physics, and modern physics has in some cases shown that the facts are a bit more complicated than assumed here. However, in general the classical concepts remain the accepted truth, just not always all of the truth as we know it now, and probably less of the truth as we will know it in the future. All the examples here actually work: we can use them to get a reasonable prediction of what will happen next in the game.
There is some subtle fine print in this discussion of the nature of physics and science, but such considerations tend to range into the atmospheric. There being no reason to sidetrack the reader into such confusions up front, they are discussed as a footnote in the last chapter of this document.
BACK_TO_TOP* To get started in physics, the first concept is that of "space", the domain in which objects -- ball bearings, billiard balls, cannonballs, bowling balls, bricks, bullets, bombs, rockets, spacecraft, cars, trucks, toys, amusement park rides, anvils, planets, and the other usual props of physics examples -- exist and operate.
In physics, space is typically defined in "Cartesian coordinates", a framework set up to measure the location of an object along X, Y, and Z coordinates. The point where these coordinate axes come together, the "origin", is generally defined to be convenient to the problem at hand. In the metric system, spatial dimensions are generally described in meters, though for very large distances, light-years are often used instead. Space can be thought of as the three-dimensional "game board" in which physical processes are performed.
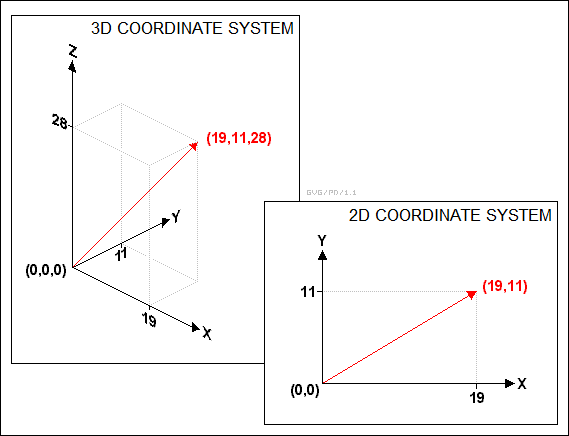
Let's consider a simple example, involving a scientist named Bob, of the comedy team of Alice & Bob, popular stars of technical examples. If Bob's in a building, his location could be described using the first-floor entrance as an origin. He could be 19 meters beyond the entrance, 11 meters to the left of the entrance, and (assuming the building has multiple floors), 28 meters above the entrance. Bob's location could then be given as:
( X, Y, Z ) = ( 19, 11, 28 )
This triplet of numbers defines a three-dimensional "vector" defining Bob's location. This vector could be thought of as an arrow that points straight from the entrance of the building to his location. A vector has a direction and a length (or magnitude). This is in contrast with the more familiar "scalar", or "undirected", quantities, such as temperature, that only have a magnitude. In the building example, the magnitude is the straight-line distance from the entrance to Bob's location. The magnitude can be given by the Pythagorean theorem as:
SQRT( X^2 + Y^2 + Z^2 ) = SQRT( 19^2 + 11^2 + 28^2 ) = 35.6 meters
For many simple physics problems, it is only necessary to describe them in two dimensions, as XY coordinates. For a common example, for practical purposes the balls on a pool table only move in two dimensions. Such a system is sometimes called "planar". Going back to Bob wandering around in a building, then if the building had only one floor, then Bob could be located just with XY coordinates:
( X, Y ) = ( 19, 11 )
This is still a vector, with a direction in the plane and a magnitude, which by the Pythagorean theorem is:
SQRT( X^2 + Y^2 ) = SQRT( 19^2 + 11^2 ) = 22.0 meters
In some cases, it is more convenient still to describe a physics problem in one dimension, for example the interactions of ball bearings colliding along a set of rails. If Bob were in a long straight hallway, his location could be given merely by a single X value, say of 19 meters. This can be regarded as a vector, with the direction being only positive or negative.
It is also useful in some circumstances to consider three-dimensional physics in terms of "polar coordinates", in which the location of an object is defined by a distance from the origin of the coordinate system, along with an angle defining "azimuth" (rotation in the horizontal plane) and an angle defining "ascension", "altitude", or "elevation" (all three being equivalent terms for rotation in the vertical plane). In two dimensions, this reduces to a length and an angle. A full description of vector math is beyond the scope of this document; the point here is simply to introduce the concept.
BACK_TO_TOP* The concept of location in a coordinate system is closely related to another concept in physics, known as "displacement". This is just the vector that describes the change in location of a moving object. It doesn't say anything about how it got from place to place or how fast it did it, it just gives the difference in location.
* Given a coordinate system that defines the location or displacement of objects, we can then discuss their movement in that coordinate system, and the changes in their movement, such as moving faster, moving slower, or changing direction. The movement of objects is known as "velocity", or displacement per time. Incidentally, velocity is not exactly the same thing as speed. Velocity is a vector quantity: it is speed in a specific direction. The term "speed" is a scalar quantity, used when the direction isn't important. Changes in that movement are known as "acceleration", or changes in velocity per time; acceleration is also a vector quantity.
In standard metric units, velocity is defined in terms of "meters per second", while acceleration is given in "meters per second squared". For example, if Bob steps out the door of his laboratory onto the lawn and drops a brick, it of course accelerates downward into the grass at an increasing velocity, due to the force of gravity on the brick. The concepts of "force" and "gravity" will be defined in a bit more detail later, but for now the reader is assumed to have a broad understanding of them.
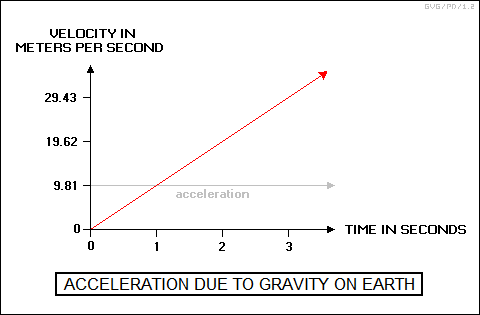
An object falling to the ground on the Earth accelerates at a constant rate of 9.81 meters per second. (This value will be different on other planets, but we won't worry about that for now.) The vector direction is straight down, so we don't need to worry about vector math in this simple case. In mathematical terms:
acceleration = 9.81
Since acceleration is the change in velocity per time, then the velocity is simply the acceleration times the number of seconds:
_________________________________________________________________________ velocity = acceleration * time = 9.81 * time _________________________________________________________________________
The falling object starts out at a velocity of zero and, with constant acceleration, the value of velocity then increases in a simple straight line. After the first second, it is falling at 9.81 meters per second; after the next second, it is falling at 9.81 + 9.81 = 19.6 meters per second; after the third second, it is falling at 19.6 + 9.81 = 29.4 meters per second; and so on.
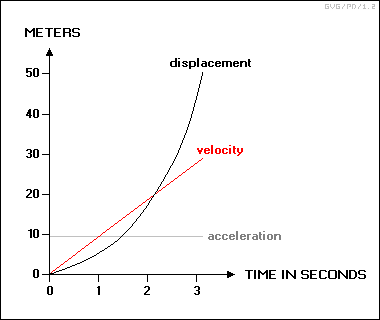
Given a constant velocity, then the displacement is the velocity times the time. This is simple to see: if an object's moving at 10 meters a second, in five seconds it covers 50 meters.
As the graph above shows, a falling object doesn't have a constant velocity, but under a constant acceleration the velocity increases in a nice straight line, and for that case we can use the average velocity times the time to give the displacement. For a straight line beginning at zero, the average velocity up to any time is half the velocity at that time. So, for constant acceleration, the displacement is:
displacement = ( velocity / 2 ) * time
= ( acceleration * time / 2 ) * time
= ( 1/2 ) * acceleration * time^2
-- or:
_________________________________________________________________________ displacement = ( 1/2 ) * 9.81 * time^2 _________________________________________________________________________
Of course, this example ignores the influence of "drag", or the resistance of air against an object moving through it. Drag is a form of "friction", which we are more familiar with as the force that resists our attempts to, say, push a heavy box across the floor. Friction is another item that needs to be discussed in more detail later, but again, the reader is assumed to understand the broad notions of drag and friction.
* Let's consider an example. Wile E. Coyote, a frustrated desert predator famed for his starring role in sadistic but extremely clever cartoons, likes to build traps to catch a quick-footed Roadrunner. In his latest trap, he hangs an anvil off a beam fixed to the edge of a cliff, with the anvil 50 meters above a trigger mechanism baited with birdseed.
As anyone familiar with the Coyote knows, he's staggeringly unlucky, and the Roadrunner simply eats the birdseed and runs off without tripping the trigger mechanism. Of course, the Coyote, again to no surprise, just has to go kick the trigger mechanism in frustration, dropping the anvil on his own head. At the risk of sounding cold-blooded, let's consider how long it took the anvil to fall 50 meters, and how fast it was moving when it hits him. We know that:
displacement = ( 1/2 ) * 9.81 * time^2
Rearranging:
time^2 = 2 * displacement / 9.81
-- and so, ignoring drag:
time = SQRT( 2 * displacement / 9.81 )
= SQRT( 2 * 50 / 9.81 )
= 3.19 seconds
So the Coyote has 3.19 seconds to build up dramatic effect before he gets flattened into a pancake. Don't worry -- he's also indestructible, so he won't be done any permanent harm. Since velocity is just acceleration times the time, then the velocity of the anvil at impact is:
velocity = 9.81 * 3.19
= 31.3 meters per second
This is about 113 kilometers per hour. This is a somewhat dubious example, since even though Wile E. Coyote's various Roadrunner traps can often be interesting examples of basic physics, we all actually know that cartoon characters follow their own peculiar laws of physics that do not match those of the real world -- for example, if duped into walking off a cliff, they will not fall until they finally look down, and will be able to desperately claw their way back up in thin air for a uselessly short time.
* This chapter has introduced basic metric units of physical measurement, such as meters, joules, watts, and so on. The following chapters will expand on this system of measurements, and to make proper use of it requires an understanding of two things: "exponential notation" and "metric prefixes".
Physics deals with quantities that may vary over a wide range, leading to very large or very small values, for example:
1,470,000,000,000 0.000000000000592
In this format, such values are unwieldy and manipulating them is error-prone. It is much more convenient to use exponential notation, with the strings of zeroes changed to a power of 10:
1,470,000,000,000 = 1.47 * 1,000,000,000,000
= 1.47 * 10^12
= 1.47E12
0.00000000000592 = 5.92 * 0.000000000001
= 5.92 * 10^-12
= 5.92E-12
It should be fairly obvious that "10^12" is 10 multiplied by itself 12 times, or 1 followed by 12 zeroes. The "E12" is a shorthand way of representing this. Similarly, "10^-12" is 1/10 multiplied by itself 12 times, and "E-12" is a shorthand format. Just to emphasize this, here's a list of powers of 10 in these formats:
1E-6 = 10^-6 = 0.000001 1E-5 = 10^-5 = 0.00001 1E-4 = 10^-4 = 0.0001 1E-3 = 10^-3 = 0.001 1E-2 = 10^-2 = 0.01 1E-1 = 10^-1 = 0.1 1E0 = 10^0 = 1 (by convention) 1E1 = 10^1 = 10 1E2 = 10^2 = 100 1E3 = 10^3 = 1,000 1E4 = 10^4 = 10,000 1E5 = 10^5 = 100,000 1E6 = 10^6 = 1,000,000
Physicists go even farther in simplifying such matters of scale using metric prefixes that specify a multiplying factor for a particular unit of measurement. For example, a "millimeter" is a thousandth of a meter, a "centimeter" is a hundredth of a meter, and a "kilometer" is a thousand meters. The standard metric prefixes include:
exo (E) = 1E18 = 10^18 peta (P) = 1E15 = 10^15 tera (T) = 1E12 = 10^12 giga (G) = 1E9 = 10^9 mega (M) = 1E6 = 10^6 kilo (k) = 1E3 = 10^3 hecto (h) = 1E2 = 10^2 deka (d) = 1E1 = 10 centi (c) = 1E-2 = 10^-2 milli (m) = 1E-3 = 10^-3 micro (mu) = 1E-6 = 10^-6 nano (n) = 1E-9 = 10^-9 pico (p) = 1E-12 = 10^-12 femto (f) = 1E-15 = 10^-15 atto (a) = 1E-18 = 10^-18
Some of these prefixes are more commonly used than others. The "mega", "kilo", "milli", and "micro" prefixes are used with many units of measurement, while the "centi" prefix is rarely encountered for anything but "centimeters", and use of the "deka" prefix is almost unheard-of. There are also sometimes special names for specific subunits of measurement -- for example, a micrometer is usually called a "micron".
Please remember that physical calculations have to be performed with consistent units. In the metric system, by default the basic units of calculations are meters, kilograms, and seconds. If units with different scales are used, such as kilometers, grams, or hours, the calculations must be consistently rescaled accordingly. This can be a maddeningly confusing and troublesome issue.
BACK_TO_TOP