
* This chapter enhances the discussion of Special Relativity by discussing relativistic mass and energy, and provides a summary of the concepts of special relativity.
* All the concepts discussed so far in this document were more or less laid out in Einstein's 1905 paper. In 1906, almost as an afterthought, he followed up with another paper that discussed mass and energy in the context of relativistic physics.
As Einstein discovered, not only did time and length change with velocity, mass did as well. Suppose Alice's starship zips by Earth at half the speed of light, to be observed by Bob on Earth. At closest approach, the starship and the Earth observer are separated by a distance D. Bob is feeling rude and hostile, and decides to shoot a cannonball of mass M at Alice so that it will hit the side of her starship at closest approach.
Bob fires the cannonball. We assume it travels at a low (non-relativistic) constant velocity V as measured by him. The flight time of the cannonball is given by:
T = D / V
Flipping this around gives the velocity as, of course:
V = D / T
Alice observes the same distance D as Bob, since it's at a right angle to her line of motion and no length contraction occurs. Alice unsurprisingly gets annoyed at being fired on, and so fires a cannonball of the same mass M and velocity V, as measured in her frame of reference, to hit the Bob's cannonball in an absolutely precise head-on collision at D/2, and bounce it back at the Earth observer in an elastic collision. (They haven't been able to afford photon torpedoes yet.)
In principle, both cannonballs hit each other at the low velocity V and bounce away at the same low velocity V. The starship's relativistic velocity Cf, imparted to the cannonball, does not directly affect the collision, since it takes place at a perfect right angle to the direction of the starship's motion. However, there's an indirect effect. Both Bob and Alice realize after they fire their cannonballs their clocks are running slow relative to each other. Since the distance D is not affected by their relative velocity, but the flight time is longer, both see the other's cannonball as moving at a velocity Vm given by:
Vm = V * SQRT( 1 - Cf^2 )
That means each should expect that their cannonball is moving faster than the other (at velocity V instead of Vm) and so will have greater momentum. Bob thinks that Alice will see her cannonball bouncing back faster after the collision, while his cannonball bounces back slower; Alice naturally thinks the reverse. The problem is that they can't both have it that way, and the only logical conclusion is that the momenta will in fact cancel out.
Since momentum is simply the product of mass times velocity, and since Bob and Alice see a different and lower velocity of the other's cannonball, then the only way out of the contradiction is to assume that the mass increases by the same factor. That is, Bob sees that Alice's cannonball has increased from its "rest mass" or "invariant mass" to a larger "relativistic mass" by the factor:
Mm = M / SQRT( 1 - Cf^2 )
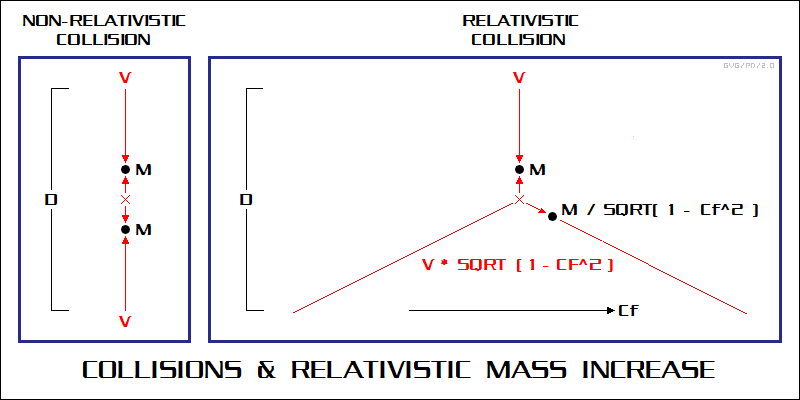
Alice sees Bob's cannonball as having increased in mass by the same amount. In other words, mass increases as an object approaches the speed of light. By the way, this formula implies that as the speed of light is approached, the mass increases towards infinity. Since force is equal to mass times acceleration, the amount of force required to get further acceleration also increases towards infinity, and the amount of energy required increases towards infinity as well.
* An analysis of relativistic mass increase leads to an interesting result. Intuitively, the fact that our starship's mass increases as more energy is pumped into it suggests a deep connection between mass and energy. In fact, an analysis of the energetics of a relativistic object (detailed at the end of this chapter) leads to:
energy = mass * speed_of_light^2
-- which is just Einstein's famous equation "E=MC2". The basic concept was not a new idea; Newton had speculated on the interconversion of light and matter, and the "E=MC2" equation was implicit in and easily derived from Maxwell's equations. Einstein was just the first to clearly articulate it. Mass-energy equivalence leads to an extension of the law of conservation of energy, in which mass-energy is conserved, with the two forms converted from one to the other under specific circumstances.
It must be emphasized that the notion of relativistic mass has some dodgy aspects, and must be regarded as no more than a workable simplification. Physicists sometimes speak of "mass-energy" or, better, "relativistic momentum" -- there being no ambiguity that the momentum has increased -- and sidestep the notion that the increase in momentum at relativistic speeds is due to an increase in mass. However, just to confuse things, particle physicists always refer to the mass of particles in terms of "electron-volts", a unit of energy.
Incidentally photons, which by definition move at the speed of light, have no rest mass, since otherwise their mass would be infinite. They do have a relativistic mass, though some physicists prefer to say they have mass-energy, or just momentum.
BACK_TO_TOP* Relativistic mass increase is a tricky subject. For example, Alice's starship accelerating towards the speed of light undergoes a relativistic mass increase as seen by Bob, with the mass being produced by the energy the starship is expending to accelerate. However, from the frame of reference of Alice, she observes the Universe moving closer to the speed of light, with the entire Universe undergoing a relativistic mass increase. Since the rest mass of the Universe is vastly greater than that of the starship, the absolute mass increase of the Universe is proportionally vastly greater as well.
That might seem to be another paradox. The energy pumped into accelerating the starship leads to an increase in the starship's mass, but the entire Universe can be perceived by Alice to grow in mass by the same proportion. Where did the energy come from to create the vastly greater relativistic mass increase of the rest of the Universe?
This turns out to be a muddled question, since essentially the same "paradox" arises in classical physics, and is easily dismissed. Suppose Alice has a scaffold structure set up here on the surface of the Earth, with a mass ten times heavier than she is set on top of it. If Alice climbs up to the top of the scaffold where she is parallel with the mass, its gravitational potential energy relative to her is zero. As Alice climbs down the scaffold, the potential energy of the mass relative to her increases the farther down she climbs. She has not in any way expended energy on the mass, she has simply used (or in the strict physical sense, lost, as she descended) energy to change her position relative to it. The relative potential energy of the mass due to Alice's change in position is ten times greater than the energy she released to change her position.
This argument also applies to relativistic physics, if the fact is understood that relativistic mass increase is an aspect of an increase in kinetic energy. Yes, if Alice is flying through the Universe at an increasing fraction of the speed of light, from her frame of reference the entire Universe gains mass. However, the energy she is expending only changes her own motion, not that of the rest of the Universe, and all she is doing is changing her energetic "perspective" relative to the rest of the Universe. As the twin paradox shows, the equivalence between different frames of reference does not imply that the two are direct mirrors of each other.
Mass-energy equivalence throws another curve into the analysis of relativistic mass. Suppose two objects of a given rest mass collide at relativistic velocities, losing their relativistic mass. A simple analysis will suggest that the combined rest mass of the two objects will be greater than their rest masses before the collision. The trick is that the excess rest mass is lost as energy in the collision, in the form of a massive explosion that would vaporize the masses into atoms.
BACK_TO_TOP* Nobody can study relativity without having the suspicion that it's all trickery, but observations do back up theory. The first observation of course was the Michelson-Morley experiment, which proved there was no ether wind. More modern experiments have failed to find any ether wind either, and no more plausible or economical theory than Special Relativity has been devised to account for that fact. The speed of light is a constant, and nobody has been able to measure any variation from that speed.
Time dilation has been confirmed in the case of certain unstable elementary particles. When moving at relativistic speeds, their decay time increases over the value at rest by the factor 1 / SQRT( 1 - Cf^2 ). Similarly, observations confirm that particles such as electrons moving at relativistic speeds are more massive than they are when at rest, by the same factor. Mass-energy equivalence has been frighteningly demonstrated by nuclear weapons.
One particularly significant proof is the relationship between magnetism and electricity. A magnetic field is caused by a moving current and exists at a right angle to that current. In fact, there actually is no such thing as a distinct magnetic force, it's just a relativistic manifestation of electric forces.
Imagine a loop of wire carrying a current. If the current is large enough and the wire is limp enough, the moving current will set up a magnetic repulsion that stretches the loop into a neat circle. In principle, the electric charge of the wire should be neutral overall, but if electrons are moving through the loop, then electrons on one side of the loop will see electrons in motion on the other side of the loop. This relative motion leads to a length contraction of the electron stream on the other side of the loop that is greater than the length contraction of the metal matrix it is flowing through. That means the other side of the loop appears to have a net negative charge and repels the electrons on the first side of the loop. The length contraction is very small, but electric forces are very powerful, and only a slight length contraction is enough to set up a tangible force.
* Other proofs of Special Relativity have been obtained through astronomical observations, and experiments with extremely precise clocks. For example, the twin paradox has been demonstrated by flying an atomic clock around the Earth in a jetliner, with the clock losing the expected amount of time relative to a clock sitting back in the lab. These proofs are a little unsatisfying, in that we really can't observe them with our own eyes and have to rely on instruments to see that they have happened.
There really isn't much choice. We don't actually perceive objects moving at high velocity in our daily environment. They're either too small, or too big and far away. If objects big enough to be seen were to pass by close enough to be observed on Earth, they would be too fast to be perceived, and in any case would destroy everything in their path as their shock wave passed through the atmosphere.
Computer graphics simulations have been designed to allow visualization of the outside world as it would appear if we were moving through it at relativistic velocities. Such programs can be tricky to write, due to optical illusions introduced by relativistic perspective. An English physicist named Eric Sheldon wrote a computer program named STELLA that shows what the Universe would look like as we accelerated through it at one gee acceleration indefinitely. This may not seem like a great acceleration, but it would be enough to push our starship so close to the speed of light that time dilation would allow us to traverse across the entire span of the known Universe in less than a lifetime.
Some of the things that we would see on this journey as we pushed closer and closer to the speed of light would be expected. We would see stars in front of us become bluer due to the Doppler shift, until they vanish into the ultraviolet. Those behind us will become redder until they are lost into the infrared.
Less intuitively, as velocity increases and the length of the Universe along the line of flight shrinks, stars in front of the ship appear to crowd closer and closer to a point directly ahead of the ship. Furthermore, time lags mean that stars that would have been observed behind the ship start to migrate into the forward field of view. Similarly, a dark region appears directly behind the ship. With increasing speed, the dark region grows as the visible Universe crowds itself in front of the ship, until at extremely high relativistic velocities it crowds itself into a small area in front of the ship and then disappears into darkness as the starlight shifts into the ultraviolet. Eventually, the low-level microwave background radiation that pervades the Universe will be shifted into the visible range, to appear as a blue dot in front of the ship.
BACK_TO_TOP* Given how devious relativity is, a short summary of the main points is useful to help the reader fit things together:
* As mentioned, although time dilation and length contraction are not optical illusions, the optical illusions created by the Doppler shift do have to be taken into consideration in examples of special relativity. There is another optical illusion that may be involved as well which, for a lack of a better term, might be called "relativistic perspective". It wasn't mentioned above, because it would have complicated the discussion without really changing anything.
Consider the examples of Alice flying at Cf = 0.8 in her 100-meter-long starship. As discussed, Bob will see Alice's starship as 60 meters long, and with the clock in the rear 267 nsec ahead of the clock in the front. However, this is only strictly true if the starship crosses Bob's line of sight at a right angle.
Suppose that Alice is flying straight towards Bob at relativistic speeds, and that her starship has a clock mounted on an arm at a right angle to the nose, with a second clock mounted on an arm on the opposite side on the rear. Suppose further that Bob takes a snapshot of the starship; it will actually show the clock in the rear being behind the clock in the front, simply because the light from the back of the ship had to travel both the length of the ship and the distance the ship moved during the time of transit of the light to the nose of the ship.
Given that the starship has a length L and a velocity of V = (Cf * C), then as far as Bob's concerned, the time T it takes for the light from the rear to reach the nose can be derived as follows:
L * SQRT( 1 - Cf^2 ) + ( T * V )
T = --------------------------------
C
C * T = L * SQRT( 1 - Cf^2 ) + ( T * V )
( C * T ) - ( T * V ) = L * SQRT( 1 - Cf^2 )
T * ( C - V ) = L * SQRT( 1 - Cf^2 )
L * SQRT( 1 - Cf^2 )
T = --------------------
C - V
For L = 100 meters and Cf = 0.8, this gives a value of 1,000 nsec. Since the clock in the rear of the starship is running ahead by 267 nsec, that means the snapshot will show the clock in the back running ( 1,000 - 267 ) = 633 nsec behind of the clock in the front. The trick of relativistic perspective will also imply that the starship seems much longer than it does from the side.
If Alice's starship is flying away from Bob, the snapshot will show the clock in the rear being well ahead of the clock in the front, since the light from the clock in the front has to travel to the rear of the starship as the starship moves forward. Much the same sort of analysis, involving simple changes of sign, gives:
L * SQRT( 1 - Cf^2 )
T = --------------------
C + V
For L = 100 meters and Cf = 0.8, this gives a value of 112 nsec; the snapshot will show the clock in the back of the starship running ( 112 + 267 ) = 379 nsec ahead of the clock in the front. From this relativistic perspective, the starship will seem shorter to Bob than it does from the side.
Once again, the idea of relativistic perspective wasn't discussed in previous sections because it would have simply created confusion, to no particularly good purpose. Although the perceived length of Alice's starship will change depending on the direction of the starship relative to Bob's line of sight, at Cf = 0.8 the starship's actual relativistic length will be 60 meters, no matter what its direction is.
The concept of relativistic perspective is a nice if not really essential thing to know. There are also some crackpots who claim that there is really no time dilation or length contraction, it's all just a trick of relativistic perspective -- but the notion wasn't even figured in to the derivations of time dilation and length contraction given in the first chapter.
BACK_TO_TOP* The explanation of Einstein's equation E=MC2 glossed over the derivations because that would have required a bit of calculus. Since some readers understand calculus, the derivation is provided here. Let's suppose that Bob is observing Alice flying in a starship of mass M moving at velocity V, and wants to determine the kinetic energy of that starship. By classical physics, that would be (( M * V^2 ) / 2 ), but since Bob knows the mass M increases with velocity, he realizes that the classical equation isn't right, and has to go back to fundamentals.
By elementary physics, the kinetic energy of a mass accelerated by a force is equivalent to the force times the distance over which that force is applied. Also by elementary physics, force is equivalent to the time rate of change of momentum. Equivalently, in calculus terms, kinetic energy is the integral of force over distance, and force is equal to the time derivative of momentum. Representing force as F, momentum as P, and remembering that velocity V is the time rate of change of distance or dx/dt, then:
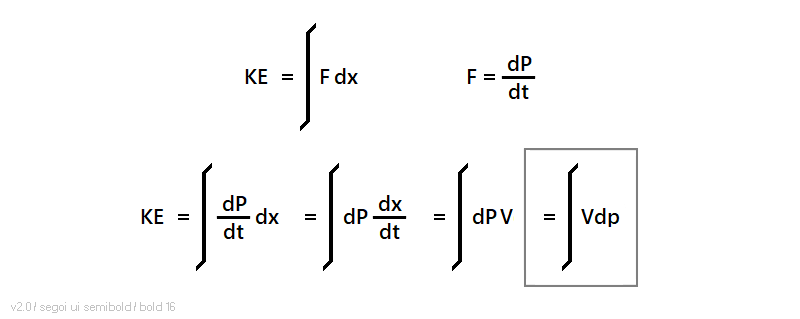
The trouble with this is that it gives momentum P as a function of velocity V, and so on the face of it, this integral is completely backwards from one that's useful in this context. However, there's a trick called "integration by parts" that can be used to turn it around (check any reasonable calculus book for details), leading to an equation for kinetic energy:
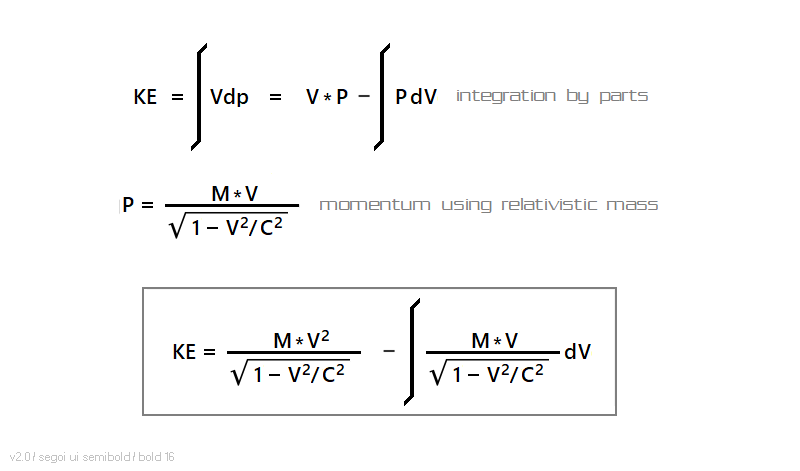
The integral that results is a simple one:
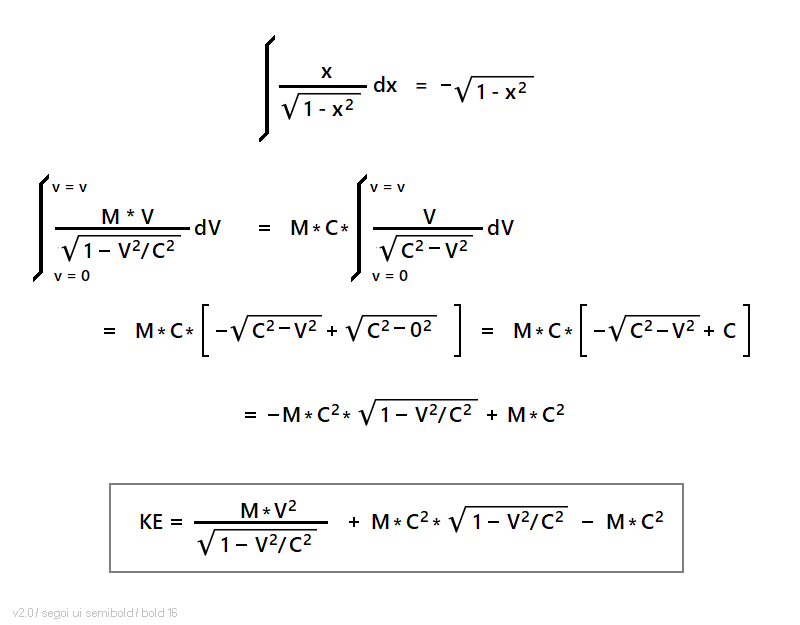
If we give the relativistic mass as:
Mr = M / SQRT(1 - Cf^2 )
-- then this equation can be rendered down as follows:
M * V^2
KE = --------------------- + M * C^2 * SQRT( 1 - V^2 / C^2 ) - ( M * C^2 )
SQRT( 1 - V^2 / C^2 )
( M * V^2 ) + ( M * C^2 * ( 1 - V^2 / C^2 ))
= -------------------------------------------- - ( M * C^2 )
SQRT( 1 - V^2 / C^2 )
( M * V^2 ) + ( M * C^2 ) - ( M * V^2 )
= --------------------------------------- - ( M * C^2 )
SQRT( 1 - V^2 / C^2 )
M * C^2
= ---------------- - ( M * C^2 )
SQRT( 1 - Cf^2 )
= ( Mr * C^2 ) - ( M * C^2 )
= ( Mr - M ) * C^2
At a velocity of zero, this gives a kinetic energy of zero, but it also implies that the incremental mass ( Mr - M ) acquired by Alice's starship at any velocity above zero by the starship's acceleration is equivalent to that mass times the speed of light squared -- or turning this around, the energy pumped into accelerating the starship is manifested as a proportional increment of mass:
( Mr - M ) = KE / C^2
The equation for kinetic energy also implies that the mass of the starship itself is equivalent to an amount of energy E, even when it's standing still:
E = M * C^2
-- and so we have now derived the most famous equation in all of physics. In 1906, Einstein could have had no clear idea of how the energy locked up in matter might be released, but it would be later understood that the ordinary matter that we deal with in our normal lives is "mirrored" by "anti-matter" with reversed electrical charges. If a mass M of matter is brought into contact with a mass M of antimatter, the two masses will annihilate each other, producing a tremendous burst of energy given by ( 2 * M * C^2 ).
* One of the seeming problems with the relativistic formulation for kinetic energy is that it doesn't appear at first glance like it reduces to the classical formulation, ( M * V^2 ) / 2, which it logically should at low velocities. Actually, it does. According to the binomial series expansion:
1 / SQRT( 1 - x^2 ) = 1 + ( 1/2 ) * x^2 + ( 3/8 ) * x^4 + ...
This means that if x is small, then the following is a reasonable approximation:
1 / SQRT( 1 - x^2 ) = 1 + ( 1/2 ) * x^2
So, for velocities much less than the speed of light:
KE = ( Mr * C^2 ) - ( M * C^2 )
M * C^2
= --------------------- - ( M * C^2 )
SQRT( 1 - V^2 / C^2 )
= ( M * C^2 * ( 1 + ( 1/2 ) * ( V^2 / C^2 ))) - ( M * C^2 )
= ( M * C^2 ) + ( M * C^2 * ( 1/2 ) * ( V^2 / C^2 )) - ( M * C^2 )
= M * C^2 * ( 1/2 ) * ( V^2 / C^2 )
= ( M * V^2 ) / 2
BACK_TO_TOP
