
* The previous chapter outlined the relativistic concepts of time dilation, length contraction, and relativistic simultaneity. All these are somewhat counterintuitive notions, and more to the point they seem to lead to paradoxes. As it turns out, if the basic concepts of special relativity are understood, the paradoxes evaporate on closer inspection.
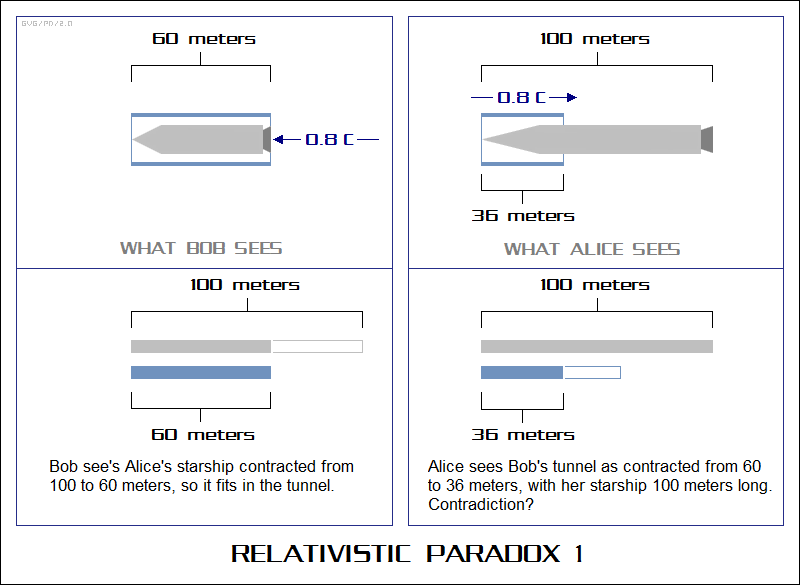
* It might seem that a consideration of relativistic time dilation and length contraction leads to completely absurd contradictions. Imagine Alice is flying a starship of length L. If Alice's starship is moving at Cf, then it is length-contracted by the factor:
Lc1 = L * SQRT( 1 - Cf^2 )
For example, if L is 100 meters and Cf is 0.8 C, then Lc1 is 60 meters.
Now let's imagine that the starship passes through a tube, a tunnel, floating in space, at rest relative to Bob; Bob sees the length of this tunnel as exactly Lc1, or 60 meters in this case. Bob will be able to observe that at one instant the starship will fit exactly into the tunnel. However, from the point of view of Alice on the starship, it is the tunnel that is length-contracted, by the factor:
Lc2 = Lc1 * SQRT( 1 - Cf^2 )
= ( L * SQRT( 1 - Cf^2 )) * SQRT( 1 - Cf^2 )
= L * ( 1 - Cf^2)
If L = 100 and Cf = 0.8 C, then Lc2 = 36 meters. That seems like an absolute contradiction -- thanks to length contraction, there's a fit as far as Bob is concerned, but as far as Alice is concerned, length contraction has just made lack of fit even worse. How can this possibly make sense?
* Before going to explain that the "Tunnel Paradox", as it's sometimes called, actually does make sense, it is useful to point out that while this example is expressed in terms of Alice's starship and Bob's tunnel, it can be and is rephrased in terms of all sorts of different pairings of two objects or sets of objects -- hoops, strings of flashing lights, pairs of starships, trains, and so on. However, no matter what the objects are, the punchline is their length. Since length is the only thing that matters, whatever the pair of objects are, measuring sticks equivalent to their length can be substituted for them and the example works precisely the same. So, reduced to simple terms, the example works like this:
It can get a little dry and confusing to explain this example using measuring sticks; most find the scenario of Alice's starship and Bob's tunnel easier to follow. The only reason to rephrase the example in terms of measuring sticks is because people trying to poke holes in relativistic theory like to rephrase the Tunnel Paradox in many different and sometimes very obscure ways -- then insist they've come up with something new, when they've just reinvented the square wheel.
The response is to ask:
Having made that substitution, the next question is:
If the answer's YES, then the example is just the Tunnel Paradox in different clothes.
BACK_TO_TOP* From a simple consideration of length contraction, we have just painted ourselves into a corner. Fortunately, there's a way out, through one of the other basic elements of Special Relativity: relativistic simultaneity. Bob can see both ends of Alice's starship fit inside the tunnel while Alice doesn't -- because as far as he is concerned, time in the rear of her starship is running ahead of time in the front.
Let's imagine that Alice has a clock at each end of her starship, and that she has synchronized the clocks. Alice, who perceives her starship at rest and the tunnel in motion, sees the Lc2 = 36-meter tunnel approaching her L = 100-meter starship at Cf = 0.8 C. Here's what Alice sees:
Alice will measure a short time interval of Td = T2-T1 from the time the nose of her starship leaves the tunnel to the time the rear of her starship passes into the tunnel. Of course, we know that Bob sees the nose of Alice's starship reach the exit of the tunnel at exactly the same instant that the rear of her starship passes into the entrance of the tunnel.
Bob can see Alice's entire starship in the tunnel at one time because, from his frame of reference, the clock in the rear of her starship is running ahead of the clock in the front. The short time interval of Td that Alice measures will give the advance of the clock in the rear as seen by Bob. Doing the algebra, the entrance of the tunnel will reach the rear of her starship after a time interval of:
L - Lc2
Td = -------
Cf * C
L - L * SQRT( 1 - Cf^2 ) * SQRT( 1 - Cf^2 )
= -------------------------------------------
Cf * C
L * ( 1 - ( 1 - Cf^2 ))
= ------------------------
Cf * C
L * Cf^2
= --------
Cf * C
= L * Cf / C
If L = 100 and Cf = 0.8 C, then Td = 267 nanoseconds (nsec), or in other words Bob sees the count on the clock at the rear of Alice's starship running 267 nsec ahead of a clock at the nose, while Alice sees the clocks as synchronized. This is a worthwhile little formula to remember: it provides a key for unlocking a number of seeming paradoxes.
There really is no paradox here. When the nose of Alice's starship reaches the exit of the tunnel, both Bob and Alice agree on that event. However, Bob sees the rear of the starship pass into the tunnel at the same time the nose reaches the exit, though as far as Alice is concerned, that won't happen for another 267 nsec.
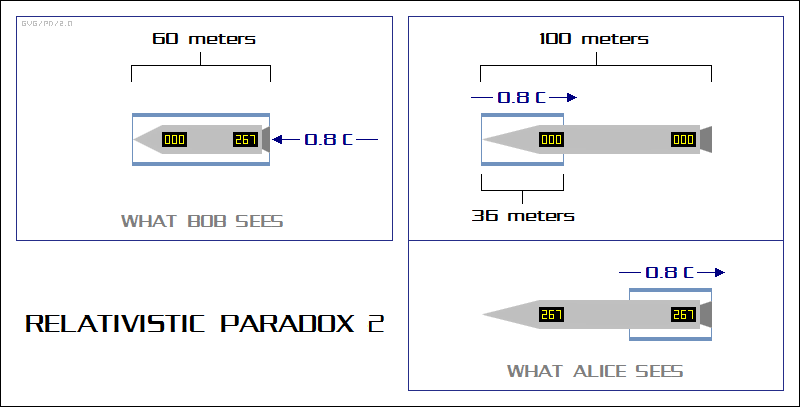
Yes, as far as relative lengths of Alice's starship and Bob's tunnel goes, there's an inconsistency: Alice and Bob have entirely contrary notions of the relative lengths of their objects. What reconciles Alice and Bob's inconsistent concepts of length are their complementary inconsistent concepts of time -- or more specifically, their different notions of things that happen at the same time.
BACK_TO_TOP* The faster Alice's starship goes, the shorter it becomes, and the more time advances in the rear of her starship. A cartoonish way to visualize length contraction is to imagine a centipede in which each successive set of legs is marching a bit ahead of the legs in front of it, forcing the centipede to pile up on itself and become shorter.
Let's take a closer look at this notion by considering light propagating from the clock in the rear of Alice's 100-meter-long starship to the clock in the front. From Alice's point of view, this is a straightforward event, with the light propagating from front to back in 100/300,000,000 = 333 nsec.
From Bob's point of view, Alice's starship is 60 meters long and moving at 80% of the speed of light, V = Cf*C = 240,000,000 meters per second. Since Bob sees Alice's starship as in motion, the forward clock will move away while the light from the rear clock is propagating forward, and so the time T Bob measures for propagation of light from the clock in the rear to the clock in the front is given by:
C * T = 60 + V * T
C * T - V * T = 60
T * ( C - V ) = 60
T = 60 / ( C - V )
= 60 / ( 300,000,000 - 240,000,000 )
= 60 / 60,000,000
= 1 microsecond
Bob knows that Alice's clock is only running 60% as fast as his, so he calculates that in her frame of reference, it takes 600 nsec for light to get from the rear of the ship to the front. Since Alice knows it only takes 333 nsec, that would seem to be a contradiction, but Bob sees the clock in the rear as running 267 nsec ahead; 267+333 = 600 nsec, and the contradiction goes away.
No matter how fast Alice is going relative to Bob, as far as she is concerned, light will always take 333 nsec to propagate from the front to the rear. However, as her relative velocity increases, Bob will calculate an ever-increasing discrepancy, and so the clock in the rear of her ship will run increasingly ahead, maintaining the equivalence of the two frames of reference. More formally, Alice sees the time for light to propagate from front to rear of her starship as:
Trfa = L / C
Since the observed time discrepancy of the clock in the rear at a velocity Cf is:
Td = L * Cf / C
-- then Bob observes that the difference in time value of the clock in the rear of Alice's starship when the pulse is emitted and the time value of the clock in the front of Alice's starship when the pulse is detected as:
Trfb = Trfa - Td
= ( L / C ) - ( L * Cf / C )
= ( L / C ) - ( L / C ) * Cf
= ( L / C ) * ( 1 - Cf )
As Cf increases, the delay Trfb will become smaller and smaller, though since Cf is always less than 1, there will always be a delay: the time value on the rear clock received at the front clock will approach that on the front clock, but it will never reach it, much less exceed it.
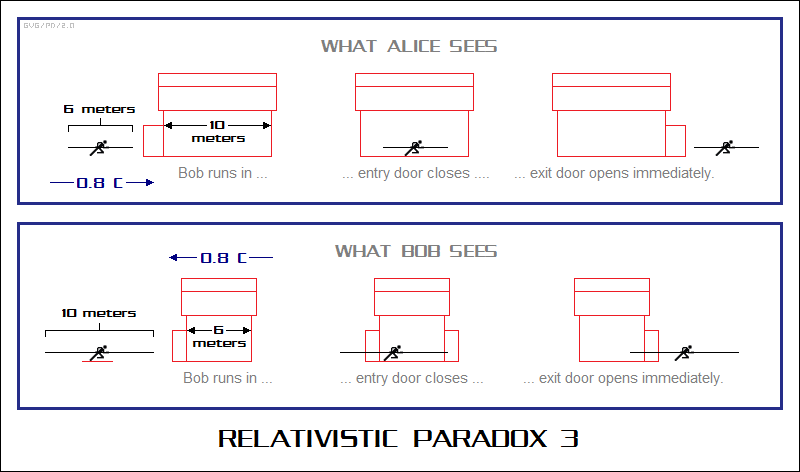
BACK_TO_TOP* Another paradox often cited in books on relativity is the "Running Man Paradox". Suppose Alice owns a barn with doors on both ends that is 10 meters long. Now suppose Bob -- who is actually the secret identity of the Flash, the fastest man alive -- is running towards the barn at 80% of the speed of light, carrying a pole 10 meters long, while Alice stands outside the barn and watches him zip past.
At Bob's speed, Alice observes the pole as being length-contracted by 60%, reducing its length to 6 meters. Bob enters the barn through an open door, while the door on the opposite side through which he intends to exit is closed. The entry door is closed automatically when the tail end of the pole clears it, and then the exit door is opened in sequence quickly enough to allow him to pass through without obstruction. This scenario makes perfect sense. Alice observes a 6-meter pole inside a barn 10 meters long, and it obviously fits inside with both the doors closed.
Now let's look at it from Bob's point of view. He can consider himself standing still in his frame of reference, with Alice's barn approaching him at 80% of the speed of light. That means that the barn is length-contracted to 6 meters, while his pole still remains 10 meters long. How can it possibly fit inside the barn with both doors closed?
It doesn't take much thought to realize this is just the Tunnel Paradox, restated slightly. The trick is that the doors are closed and opened in synchronization in the barn's frame of reference, but Bob does not see the doors as synchronized in this way. Going back to the little equation derived above:
Td = L * Cf / C
-- then if L, the length of the barn or the pole, is 10 meters, and Cf is 0.8 C, the value of Td is:
10 * 0.8
----------- = 26.7 nsec
300,000,000
From Bob's point of view, when he runs through the barn and the front of his pole is about to reach the exit door, he still has 4 meters of pole sticking out of the entry door. However, he knows that to Alice the time at the exit door is running 26.7 nsec ahead of the time at the entry door. At Cf = 0.8 C, the 4 meters of pole still outside the entry door will pass through in 16.7 nsec. He has 10 nsec to clear the entry door before it closes.
By the way, the fact that the pole actually fits into the barn in the barn's rest frame demonstrates that length contraction is not an optical illusion: the pole really is shorter in Alice's frame of reference by any means she can use to measure its length. There's also the interesting question of what happens if Bob stops inside the barn, but that is way too complicated an issue to discuss here.
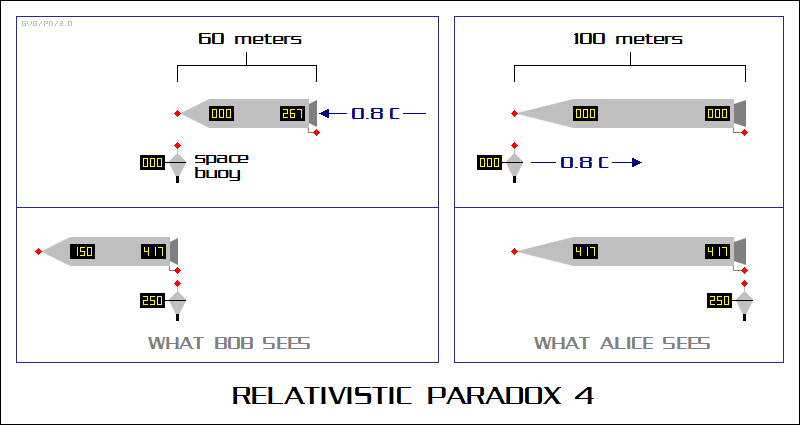
* For a third puzzle, let's go back to Alice and her 100-meter-long starship. Suppose she is moving at 80% of the speed of light past a little space buoy that Bob has set up to track her passage. Alice's spaceship is fitted with a little module on the nose and rear, and the buoy is fitted with one of the modules as well. These modules can detect the proximity of each other, using microwave beams or lasers or whatever; the specifics are irrelevant, all we have to do is assume the modules detect each other at a short enough range and react in little enough time so that the details of how it is done can be ignored. When the module on the buoy detects the module on the nose of Alice's starship flying by, it starts a timer, and when it detects the module on the rear of Alice's starship flying by, it stops the timer.
Let's see what happens in Bob's frame of reference. Alice's starship zips past him at 80% the speed of light, 240,000,000 meters per second. At this speed, the starship is contracted to 60 meters, and the buoy clocks the transit of the starship as 60/240,000,000 = 250 nsec as measured by Bob. Since Bob knows that Alice's starship is 100 meters long in her frame of reference, he can determine that to Alice the transit takes 100/240,000,000 = 417 nsec, and that is exactly what Alice does measure -- the length contraction of the space buoy being an irrelevant consideration in this example. Alice, knowing Bob's clock is running only 60% as fast as hers, also correctly knows that Bob will measure 467*0.6 = 250 nsec for the transit.
Now here's where the paradox shows up: Bob sees the transit as taking place in 250 nsec, and since Alice's clocks are running at 60% the rate of his, he calculates that Alice should only measure 250*0.6 = 150 nsec. Which is it? 417 nsec or 150 nsec?
When the rear of Alice's starship passes the buoy, the clock in the rear does read 417 nsec -- but the trick is that the clock in the rear of the starship was already at 267 nsec when the timer started counting, and by Bob's figuring it really only did advance 417-267 = 150 nsec. That seems like a wild contradiction, Bob calculating that Alice's clock is running faster than his by the same factor that it is actually running slower than his, but thanks to the sleight of hand of relativistic simultaneity it works out. Again, this is just the Tunnel Paradox rephrased, with the tunnel in effect reduced to the equivalent of two-dimensional hoop through which Alice's starship jumps, with the apparent paradox showing up as a seeming time discrepancy instead of a length discrepancy.
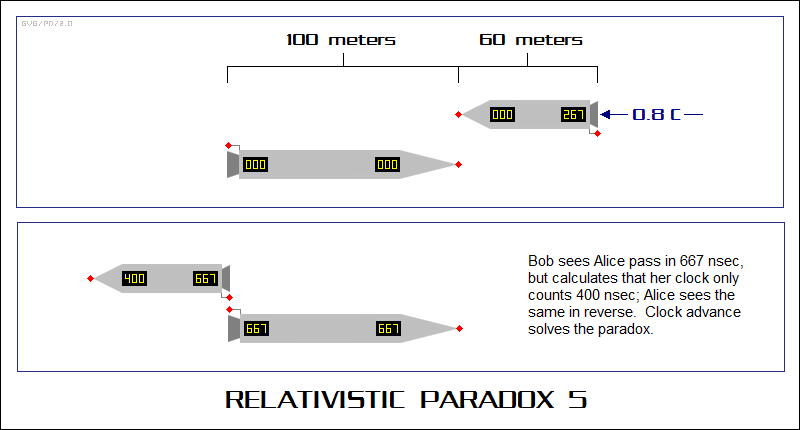
* Finally, let's pretend both Bob and Alice are flying in 100-meter starships with modules on each end, and pass each other at a relative speed of 80% of the speed of light. The modules work just as they did in the previous example. Bob starts counting time when the module on the nose of his starship encounters the module on the nose of Alice's starship, and then stops counting when the module on the rear of his starship encounters the module on the rear of Alice's starship.
In Bob's frame of reference, Alice's starship travels 100+60 = 160 meters during that interval, which gives a transit time of 160/240,000,000 = 667 nsec. Bob knows that Alice's clock is running slow by 60%, and so this amounts to 667*0.6 = 400 nsec in Alice's frame of reference. However, Alice sees exactly the same situation in reverse, believing that the transit takes 667 nsec in her frame of reference and 400 nsec in Bob's. In other words, where did the time dilation go? They're both measuring exactly the same transit time, 667 nsec, when each thinks the other should be clocking 400 nsec.
Of course, we know the answer by now. We've already calculated that the discrepancy in clock synchronization for a 100-meter starship moving at 80% of the speed of light is 267 nsec; 400+267 = 667 nsec, and the paradox goes away. This is still another variation on the Tunnel Paradox, just one that is set up to look the same from both sides. Incidentally, since this particular example has the two starships flying at a relative velocity of 80% of the speed of light, that raises the interesting question of what we would observe as the velocity of each. Enough to say here that it isn't, say, 40% of the speed of light in the opposing directions; it's trickier than that, a matter discussed below.
There are many variations on these puzzles -- a moving block falling through a hole is another common one -- but after performing enough of them, they all are seen as alterations of the Tunnel Paradox. Readers who find them amusing are encouraged to look through formal texts on relativistic physics, which often include sets of such problems.
BACK_TO_TOP* Relativistic theory leads to another apparent paradox. Suppose Alice and Bob are twins. Alice flies to the stars in a starship moving at a good percentage of the speed of light ("relativistic" speed) while Bob stays at home. When Alice comes back to Earth, she will be younger than Bob.
For example, suppose that Alice and Bob are both 20 years old when Alice sets out in a starship to travel to the planet Minbar, 10 light-years away, at half the speed of light. She spends a negligible amount of time at Minbar, and then comes back to Earth at half the speed of light. Her time-dilation factor, given Cf = 0.5, would be:
1 / SQRT( 1 - 0.5^2 ) = 1.15
Her trip would take 40 years as far as Bob back on Earth was concerned, but only 40/1.15 = 34.6 years as far as Alice was concerned. Bob would be 60 years old; Alice would not quite be 55 years old.
This is known as the "Twin Paradox", and it immediately leads to two objections over two issues:
The equivalence issue is the critical one in the Twin Paradox. The resolution is that the two scenarios, though equivalent in the strict sense, are not the same. The common preconception is that the two scenarios mirror each other; actually, they're much more analogous to a balanced plank. Imagine a scenario where the plank has 1 kilogram on one side of the balance point and 3 kilograms on the other; then if the 1-kilogram weight is 1 meter from the balance point, the 3-kilogram weight will have to be 3 meters from the balance point for the plank to stay level. Everything is neatly balanced, but it doesn't look the same on the two sides of the balance point. That's a very broad analogy to relativistic physics; instead of balancing weight and distance of two elements, we're talking much less intuitively about balancing time and distance for two elements.
To Bob back on Earth, Alice's starship is moving at half the speed of light, and only her starship is length-contracted. To Alice, the rest of the Universe is moving at half the speed of light, and the rest of the Universe is length-contracted: the distance to Minbar is only 10/1.15 = 8.66 light-years. Alice is taking a trip through a Universe that appears length-contracted to her, and so a trip at half the speed of light takes a shorter time. In fact, it was the necessity to ensure that the Alice and Bob's clocks balance out that was used in the previous chapter to introduce the notion of length contraction in the first place. Alice is out of context with Bob's Universe; lengths in that Universe have grown shorter as she sees them, with her clock ticks stretching out to compensate.
However, that leads straight to the slow clock issue. How can Alice and Bob see each other's clock running slow and come up with different timing? The resolution is that they don't always see the other's clock running slow. Why don't they? That's because, even though time dilation is not an optical illusion, optical illusions are also involved in the Twin Paradox.
The phenomenon of relativistic time dilation was derived in an earlier section in the case of a starship moving across our line of sight, in which the clock appears to run more slowly. However, that does not mean that the clock will be seen to run slower in all circumstances, which is a common misconception about Special Relativity. If Alice's starship is moving toward Bob, her clock will seem to run faster than his. If Alice's starship is moving away from Bob, her clock will seem to run even more slowly than it would if her starship were running across his line of sight.
* Discussion of this phenomenon requires an understanding of the "Doppler shift", which was well understood by classical physicists at the beginning of the 20th century. It is the change in pitch caused by the motion of an object. If a train approaching at high speed blows a whistle, the pitch of the whistle is higher than it would be if the train were at rest. Similarly, if the train is moving away, the pitch of the whistle is lower. If the time of the period of the whistle's wavelength when the train is at rest is T and the period when the train is moving at velocity V is Tm, then if the speed of sound is given by S, the ratio of the change in period due to the Doppler shift is given by:
Tm / T = ( 1 - V/S )
-- if the train is approaching. If the train is moving away, the ratio is given by:
Tm / T = ( 1 + V/S )
The classical Doppler shift can be redefined to apply to light with a minor change in variable definitions:
Tm / T = ( 1 - Cf ) ! if approaching Tm / T = ( 1 + Cf ) ! if receding
The classic Doppler shift is not correct at relativistic speeds, since the time dilation factor applies and has to be also multiplied in. This gives:
1 - Cf
Tm / T = ----------------
SQRT( 1 - Cf^2 )
Squaring both sides of the equation gives:
( 1 - Cf )^2
( Tm / T )^2 = ------------
1 - Cf^2
( 1 - Cf )^2
= -----------------------
( 1 - Cf ) * ( 1 + Cf )
( 1 - Cf )
= ----------
( 1 + Cf )
So, for an approaching starship, the relativistic Doppler shift is:
Tm / T = SQRT(( 1 - Cf ) / ( 1 + Cf ))
With a simple change in sign, for a receding starship, the relativistic Doppler shift is:
Tm / T = SQRT(( 1 + Cf ) / ( 1 - Cf ))
If we have a clock that emits a pulse of light on every tick, the pulse / tick period will decrease if the clock is approaching and increase if it is receding. More generally, the Doppler effect causes the light of objects approaching us to be reduced in period, or equivalently increased in frequency, becoming bluer and more energetic, or "blueshifted". Similarly, the light from objects moving away from is increased in period, or equivalently reduced in frequency, becoming redder and less energetic, or "redshifted". We can use the terms "blueshift" and "redshift" as a convenient shorthand for describing the two Doppler effects.
* Now let's suppose that Bob's clock on Earth and a clock on Minbar are synchronized with each other by transmissions of coded timing signals. Although events that are synchronized in one frame of reference are not necessarily synchronized in another, the clocks can still be synchronized with each other in the same frame of reference. Assuming that Earth and Minbar are exactly 10 light-years apart, each will receive clock signals that should be exactly 10 years old and can adjust their clocks accordingly.
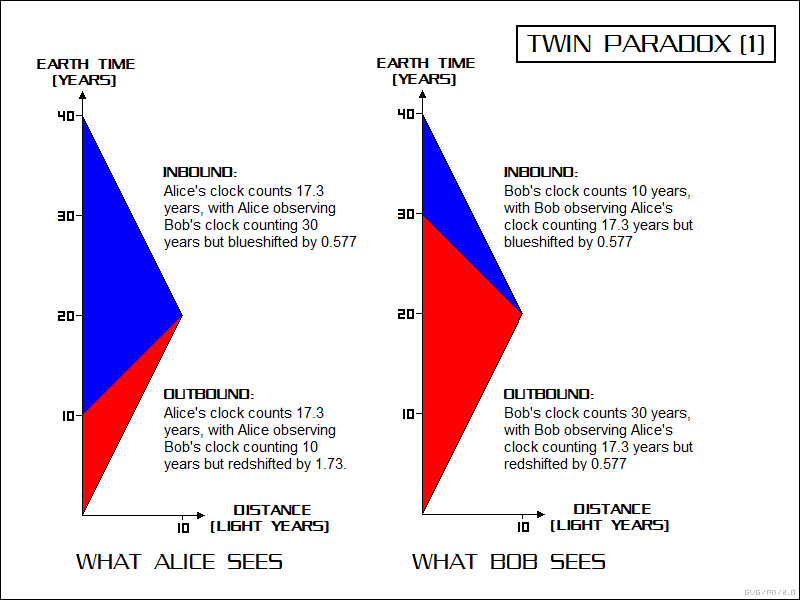
Just before Alice leaves the Earth at some arbitrary "time zero" Tz, she will read the signal from the clock on Minbar and find that it gives a value of Tz-10 years. She knows that it will take 20 years in Bob's frame of reference for her to reach Minbar, so she knows that when she arrives at Minbar the clock there will read Tz+20 years. She will observe the clock on Minbar count through 30 years during the course of her journey, while her own clock only counts through 17.3 years.
This means that she sees the clock on Minbar "blueshifted" by the Doppler effect, running fast by a factor of:
Tm / T = ( 17.3 / 30 ) = 0.577
This is exactly what would be predicted by the relativistic Doppler effect:
Tm / T = SQRT(( 1 - Cf ) / ( 1 + Cf ))
= SQRT(( 1 - 0.5 ) / ( 1 + 0.5))
= 0.577
When Alice ends her negligibly brief stay on Minbar, she turns around and heads back home. By exactly the same logic, the signal from Bob's clock arriving on Minbar from Earth will be 10 years out of date, and she knows Bob's clock will advance 30 years while she flies home at half the speed of light. This is exactly the same scenario as occurred on the outbound leg of the journey, and it works out in exactly the same way.
Of course, while Alice was traveling away from the Earth on the outbound leg of the voyage to Minbar, she was picking up the signals from Bob's clock. When she left, the signal from Bob's clock was reading a value of Tz, and when she arrived at Minbar, the signal was reading as Tz+10. As she went from Earth to Minbar, she observed Bob's clock as "redshifted" by the Doppler effect by a factor of:
Tm / T = ( 17.3 / 10 ) = 1.73
Again, this is exactly what would be predicted by the relativistic Doppler effect:
Tm / T = SQRT(( 1 + Cf ) / ( 1 - Cf ))
= SQRT(( 1 + 0.5 ) / ( 1 - 0.5))
= 1.73
So .... during the course of her journey, Alice reads Bob's clock counting over 10 years at a slow rate and over 30 years at a fast rate, and she sees that Bob's clock has indeed counted through 40 years while hers has only counted through 34.6 years.
Incidentally, this is a somewhat artificial scenario, since it assumes that Minbar and Earth are motionless relative to each other and that clocks between the two planets can be effectively synchronized -- but given the fact that the relative motions of star systems and planets within such a cosmically short distance are far below the speed of light, the error factor in the analysis remains insignificant.
* OK, that shows how the scenario works from Alice's point of view. Now we need to consider how the same scenario appears from Bob's point of view. Let's suppose that Alice's starship also has a communications system to allow it to relay its current clock time back to Bob. As Alice flies to Minbar, Bob observes her "redshifted" clock running slow by a factor of 1.73, and when she turns around and comes back, he observes her "blueshifted" clock running fast by a factor of 0.577.
As noted, however, he will not observe Alice's clock as "redshifted" and "blueshifted" for the same amount of time:
In sum, the observations between the clocks in the two frames of reference work out because Bob, at the start and end point of Alice's round trip, sees Alice's clock running slow 75% of the time and running fast 25% of the time, while for Alice the proportions are exactly 50% each.
* A graph known as a "spacetime diagram" or "Minkowski diagram" -- after Hermann Minkowski (1864:1909), a Russian expatriate who had been one of Einstein's instructors at the Swiss Federal Institute of Technology (ETH in its French acronym) in Zurich -- can be used to help visualize the scenario. It's just a graph with time on the vertical axis and space on the horizontal axis, with the time and space defined for one observer's frame of reference, in this case the Earth's.
If the time axis is measured in years, the space axis is measured in light-years, and the two axes have equal increments, then light always travels at a 45-degree path on the diagram. An object at rest in the Earth's frame of reference follows a vertical path, since it passes through time but not space, while an object moving closer and closer to the speed of light approaches the 45-degree angle. Minkowski diagrams are often used in texts on relativistic physics.
* There's still a problem left with the slow clock issue, however. Alice flatly knows, factoring out the Doppler shift, that the clocks on Earth and Minbar are running slow as far as she's concerned, but those clocks still end up running faster, counting off more time, in the end.
During the trip to Minbar, Alice, by her own clock, determines that 17.3 years have passed. However, she knows that, in spite of the fact that "blueshifting" makes the clock on Minbar appear to run fast, it is actually running slow due to time dilation by the factor of 1.15, and so it only counts 17.3/1.15 = 15 years during the course of her outbound journey. Since the clocks on Earth and Minbar are synchronized in their frame of reference using coded signals, then when Alice departed from Earth the clock on Minbar read Tz. When she arrived at Minbar, it read Tz+20 -- not Tz+15 as she might have expected.
The answer should be apparent, though maybe not obvious, from a knowledge of how relativistic simultaneity works. Notice the qualification that the clocks on Earth and Minbar are synchronized in their own frame of reference. Once Alice gets up to speed, they are no longer synchronized in Alice's frame of reference, with the difference in synchronization is given by, as before:
Td = L * Cf / C
If L is specified in light-years and Td in years, this simplifies to:
Td = L * Cf
Given that L is 10 light-years and Cf is 0.5 C, that means that as far as Alice is concerned the clock in Minbar is running 5 years ahead through the entire outbound journey. It times through 15 years during her trip, and ends up at a value of 20 years.
By the same logic, while Alice spends 34.6 years on her interstellar round trip, she knows that Bob's clock is running slow by a factor of 1.15 and so only counts through 34.6/1.15 = 30 years. The trick is that Alice got 5 years out of sync with the rest of the local Universe, and when she turns around she gets out of sync with it by another 5 years, for a total of 10 years, which means that when she arrives back home Bob's clock has counted 40 years since her departure.
This is the ultimate reply to the protest: "How can Bob and Alice both know for a fact that each other's clock is running slow but end up with different results?" Yes, they do know for a fact that each other's clock is running slow, but there's a question of synchronization involved, something along the lines of the Tunnel Paradox. As Alice flies to Minbar, she knows the clocks there are running slower than hers, but Minbar's clocks have a five-year jump on hers, and so when she arrives there, time has still passed more swiftly than it did for her. The same effect applies on her return journey.
BACK_TO_TOP* The Twin Paradox sounds so dodgy that it's worthwhile to summarize how it works. A "question and answer" format works well in this case:
* The explanation of the Twin Paradox given above used a simple straight-line round trip, but it works out the same no matter what "flight plan" Alice follows, as long as she flies at half the speed of light. If Alice went into orbit and spun dizzily around the Earth at half the speed of light for 40 years by Bob's clock, she will have only aged 34.6 years at the end.
It is easy to demonstrate this: if a set of space stations were placed in a ring around the Earth, motionless relative to the Earth and with their clocks synchronized to Bob's Earth clock, then Alice could take her ship from station to station in a straight line until she traversed the entire ring. The scenario for each jump from station to station would be the same, except for distances, as it would be if she flew from Earth to Minbar. The same sort of reasoning could be used for any flight path of any configuration, with Alice performing straight-line flights from station to station conveniently arranged along the flight path. Accounting for the readings of Bob's clock and Alice's clock is trickier, but the accountings will always have to add up.
* Incidentally, some sources tend to give the impression, maybe not deliberately, that the Twin Paradox is due to Alice flying away and coming back while Bob stays put, but though that's not exactly wrong, it's misleading: the Twin Paradox is more properly due to the fact that Alice is flying through a length-contracted Universe, while Bob simply sees that Alice is flying in a length-contracted ship. The fact that Alice flies away and comes back while Bob stays put merely explains how their accountings of clock ticks balance out.
Suppose that instead of flying 10 light-years to Minbar, Alice flies 20 light-years at half the speed of light to the planet Zahadum, where she plans to settle with no thought of coming back home to Earth. When Alice departs, Bob sends a message to Zahadum telling the planet's high council that Alice is 20 years old and that she will arrive in 40 years' time -- by a remarkable coincidence, a year on Zahadum is the same length as a year on Earth. The high council receives the message 20 years later and realizes that Alice will arrive in 20 more years.
Their local customs require that Alice be greeted by someone her own age, and so they select Dot, who happens to be 40 years old. 20 years later, Alice arrives to meet Dot, who is now 60 -- but Alice is still not quite 55 years old. Alice's trip was one-way, but the Twin Paradox applied just as much as if she had gone to Minbar and then returned to Earth.
* Sources also sometimes say that the Twin Paradox is due to the fact that Alice undergoes acceleration while Bob does not. This is also not exactly wrong, since Alice has to accelerate to reach half the speed of light and get out of context with Bob's Universe, but it's misleading as well.
Let's go back to the example of Alice's ship passing a space buoy. Suppose Bob has a space buoy near Earth and Dot has a space buoy near Zahadum. Alice comes zipping past Bob's space buoy at half the speed of light, and when she does so, she relays her current age of 20 to the buoy. Bob then relays Alice's age on to Zahadum, and 40 years later (as Bob and Dot read the clock) Alice zips by Dot's space buoy, once again relaying her age. Although Dot is 60, Alice will report her own age as under 55, as before. No accelerations were directly involved in this scenario.
BACK_TO_TOP* As described above, in the Twin Paradox, Alice goes to Minbar 10 light-years away at 50% of the speed of light, a journey that takes 40 years, 20 years each way, as far as Bob is concerned -- but only 34.6 years, 17.3 years each way, as far as Alice is concerned. This imbalance seems illogical on the face of it, since by the equivalence principle, it might seem just as reasonable to think Alice would age 40 years, while Bob only ages 34.6.
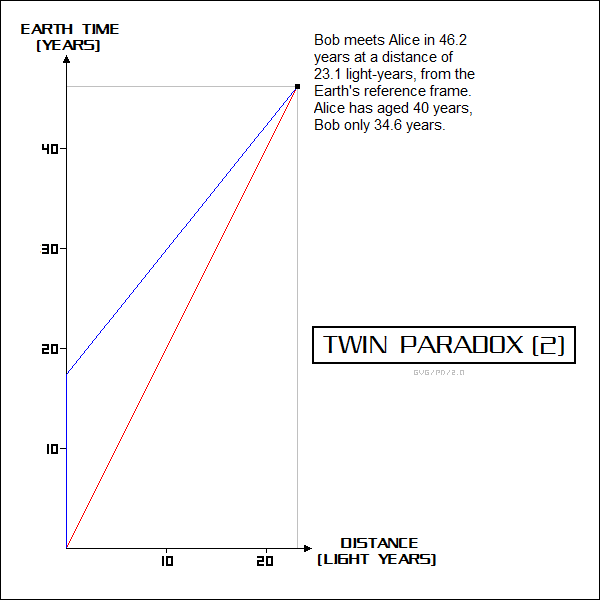
As explained, that's not true -- Alice is traveling through a length-contracted Universe while Bob is not -- but it does lead to the interesting question of how the scenario might be rearranged so that Bob actually does age less than Alice. In this revised scenario, Alice's starship flies at 50% of the speed of light, without stopping and turning around, while Bob leaves Earth at the "turnaround time" of 17.3 years and takes a faster starship to catch up with Alice after she flies for 40 years by her clock. Assuming, conveniently for the moment, that Bob only takes 17.3 years to catch up by his clock, then the Twin Paradox would be neatly reversed: Alice ages 40 years, Bob only 34.6 years.
Bob has to do some calculation to figure out how fast he needs to go to make the rendezvous. From his point of view, Alice's clocks are running slow by a factor of 1.15. That means that the time of rendezvous will actually be 40*1.15 = 46.2 years after Alice's departure, by an Earth clock, and so the rendezvous point will be 0.5*46.2 = 23.1 light-years away. Since Bob takes off 17.3 years after Alice's departure, he calculates that he will have to catch up with Alice in:
46.2 - 17.3 = 28.9 years
-- as measured by an Earth clock. Since the rendezvous point is 23.1 light-years away, that means that Bob must fly from Earth at:
23.1 / 28.9 = 0.8 C
-- or 80% of the speed of light, to make the rendezvous.
That trip will take 28.9 years by an Earth clock, but once Bob takes off in his starship at 80% of the speed of light, time slows down by a factor of 0.6, and so by his clock it actually only takes:
28.9 * 0.6 = 17.3 years
-- to catch up, just as conveniently assumed. In this scenario, Alice sees the Earth flying away from her at 50% of the speed of light for 20 years, reaching a distance of 10 light-years, with Bob then flying back to her at 50% of the speed of light over 10 light-years for another 20 years. When the two rendezvous, Bob has only aged 34.6 years and Alice has aged 40 years. The Twin Paradox has indeed been reversed.
Of course, the accounting for Alice and Bob's clock ticks works out as well:
* Consideration of this scenario leads to another seeming paradox: from Alice's point of view, she's standing still, while the Earth is flying away at half the speed of light and Bob is approaching at half the speed of light. From Alice's point of view, she might think that the speed of Bob relative to the Earth is the speed of light -- but it's actually only 0.8 C.
In fact, this general scenario holds no matter how high a fraction of the speed of light Alice observes for the two velocities: they don't add up linearly, the sum of the two will never exceed the speed of light. Suppose the Twin Paradox scenario is changed to Alice flying 10 light-years to Minbar at Cf = 0.9 C. That means that Alice's round trip time would be 20/0.9 = 22.2 years as far as Bob is concerned, though only 9.69 years as far as Alice is concerned. Now once again consider Bob leaving at 9.69/2 = 4.84 years in the Earth's frame of reference and trying to catch up with Alice after a total of 22.2 years of flight in her frame of reference.
Her clocks are running slow relative to an Earth clock by a factor of 2.29, so the actual rendezvous time will be 2.29*22.2 = 51 years after Alice's departure by the Earth clock, by which time she will have traveled 51 * 0.9 = 45.9 light-years. Bob has to catch up in 51-4.84 = 46.1 years by an Earth clock, meaning he has to travel at 45.9/46.1 = 0.994 C to make the rendezvous. Since Bob's clock is running slow by a factor of 9.53, that means it only takes him 4.84 years by his own clock to make the rendezvous.
Although Alice would see the Earth and Bob moving in opposite directions at 0.9 C, their relative velocity is only 0.994 C, not 1.8 C as Alice might calculate. The same exercise can be performed for any other values of Cf; Bob will always end up flying slower than the speed of light relative to Earth.
* This can be thought of as the "Addition Paradox", or just "relativistic velocity addition". If Alice observes two objects flying away from each other at a speed of 0.5 C relative to her, she might assume they have a relative speed of the speed of light -- but simple addition doesn't actually work; as far as the two objects are concerned they're only flying away from each other at 0.8 C, not the speed of light.
Similarly, If Alice observes two objects flying away from each other at 0.9 C, their relative velocity as far as they are concerned is only 0.994 C, not 1.8 C. Of course, the same relative velocities are observed if the two objects are approaching each other, since the only change has been in their positions.
In more general terms, consider two objects moving at Cf1 and Cf2 as observed from a third frame of reference. There is actually a simple equation to give the relative velocity Cf12 as observed in the frames of reference of the two objects; it can be derived with a little calculus, but in the interests of simplicity, the details are ignored here to just give the result:
Cf2 + Cf1
Cf12 = -------------
1 + Cf2 * Cf1
-- if they are moving in opposite directions. Of course, it's also nice to be able to figure out the relative velocity of the two objects if they are traveling in the same direction -- for example, to allow an Earth observer tracking Bob in his effort to catch up with Alice to determine the velocity of Bob and Alice relative to each other. Not surprisingly, that equation just involves changes in signs:
Cf2 - Cf1
Cf12 = -------------
1 - Cf2 * Cf1
For example, if Alice observes the Earth and Bob moving in opposite directions at Cf1 = Cf2 = 0.5 C, then their relative velocity actually is:
0.5 + 0.5
Cf12 = -------------
1 + 0.5 * 0.5
= 1 / 1.25 = 0.8 C
-- as expected. Push the relative velocity up to 0.9 C and the equation gives 0.994 C.
If an Earth observer watches Bob at Cf2 = 0.8 C trying to catch up with Alice at Cf1 = 0.5 C, then their relative velocity is:
0.8 - 0.5
Cf12 = -------------
1 - 0.8 * 0.5
= 0.3 / 0.6 = 0.5 C
-- again, as expected. Change the scenario to Bob flying at 0.994 C to catch up with Alice flying at 0.9 C, and the result is 0.9 C.
Repeating the calculation for two objects flying at the same speed in different directions for a range of speeds to determine the apparent and actual relative velocities gives:
speed apparent actual
____________________________
0.1 0.2 0.198
0.25 0.5 0.47
0.5 1.0 0.8
0.75 1.5 0.96
0.9 1.8 0.994
0.95 1.9 0.999
0.99 1.98 0.99995
____________________________
speeds in values of Cf
These equations are strictly one-dimensional, working along a straight line, but equations can be expanded to two or three dimensions using the same principles, though that's something that needs to be discussed in a more advanced document.
BACK_TO_TOP