
* The theory of Special Relativity does not require advanced math to understand, though its concepts are tricky. This chapter lays out the basic principles of Special Relativity as simply as possible. These principles will seem to lead to contradictions and paradoxes, but such difficulties should be ignored for the moment; they're discussed in the next chapter.
* Albert Einstein's theory of Special Relativity was derived from two principles. The first was "Galilean Relativity", the simple principle established by Galileo Galilei (1564:1642) that there was no way to distinguish a state of uniform motion from a state of rest. The laws of motion appear the same to observers in a cube moving uniformly as they do if the cube were sitting still. In terms of modern physics, the laws of motion are said to be "gauge (measurement) invariant".
This simple, almost intuitive concept leads to the relativistic "equivalence principle": if two objects are moving relative to each other, it is just as valid to regard the first as stationary and the second as moving, as it is the reverse. For example, suppose two friends, Alice and Bob, are both in their own glass cubes moving relative to each other in empty space. Alice will believe she is standing still and Bob is moving; Bob will believe he is standing still and Alice is moving. Modern physics describes this situation as a "symmetry". This all may sound very exotic, but Galilean relativity is absolutely straightforward, merely establishing that motion is a relative concept: motion relative to what?
The second principle arose from considerations of the observed behavior of light. This principle was articulated by Albert Einstein (1879:1955) as a postulate in response to a very difficult problem in physics. What Einstein said was that the speed of light is an absolute constant. Why he said this, and why it was such an astonishing thing to say, requires a little explanation.
* In the later half of the 19th century, the Scots physicist James Clerk Maxwell (1831:1879) devised a set of equations describing electricity and magnetism that suggested that electromagnetic energy could be transmitted in the form of waves. These electromagnetic waves were quickly identified with light and invisible forms of electromagnetic radiation, such as radio waves.
In classical physics, a wave is a disturbance through a propagating medium. For example, a sound wave consists of variations in pressure propagating through the air, while a water wave consists of variations in height of water propagating across a body of water. If electromagnetic radiation was in the form of waves, then by classical thinking it had to be a disturbance of some sort of propagation medium. The only problem was that light propagated through free space where nothing of substance could be detected. Physicists therefore suggested the existence of a "luminiferous (light-bearing) ether" as the propagation medium.
Although the ether was invisible and undetectable, it was thought to fill the entire Universe, with the planets and stars moving through it unimpeded. This implied that the ether established an "absolute frame of reference" for the motion of objects through it. The ether was universal and fixed, and so the motions of heavenly bodies could in principle be measured relative to it.
By this time, the speed of light had been determined to be very close to 300,000,000 meters per second. The question quickly arose: just how fast is the Earth moving relative to the ether? Experiments were conducted to determine the velocity of the "ether wind". The most famous of these experiments was conducted by the brilliant American experimental physicist Albert A. Michelson (1852:1931) and his colleague Edward W. Morley (1838:1923), who had established a solid reputation as an experimentalist in determining the abundances of various elements.
* The "Michelson-Morley experiment" was an early application of an "optical interferometer". If two waves propagate through the same medium, they can constructively or destructively interfere with each other. For example, if two water waves of the same frequency propagate over water, they could be out of phase and cancel out to calm the water, or add up to make the waves higher. Two beams of light can similarly interfere with each other, leading to constructive interference, resulting in brightness; or destructive interference, resulting in darkness.
An optical interferometer operates by splitting a beam of light with a half-silvered mirror, running the split beams through two paths or "arms" at a right angle to each other, reflecting the two beams back together and summing them in an eyepiece, then observing the interference effects between them, manifested as a pattern of alternating light and dark "fringes". The split light beams can be "bounced" back and forth in the arms to increase the effective path length. Shifts in light propagation through the two paths are easily detected. Optical interferometry is extremely sensitive, and is now often used an as element in highly accurate sensor and instrument systems. The illustration below shows a simplified Michelson interferometer:
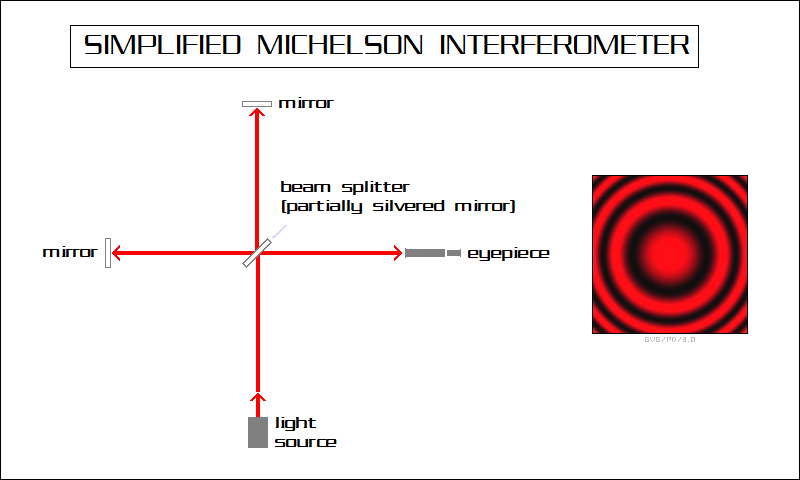
The Michelson-Morley interferometer was set up in the basement of a stone building; it was built on top of a heavy marble slab to ensure stability and reduce vibration. The slab could be rotated around the vertical axis on a thin film of mercury. A light beam was split, reflected along two paths at right angles to each other, and then summed again to generate interference effects.
If the reflected light beam was in the direction of the ether wind, the velocity of the ether wind would be subtracted from the velocity of light in one direction, then added in the other; there would be no net effect on the round-trip time. However, if the reflected light beam was crossways to the ether wind, then the effect of the ether wind would be to slow the beam down whether it was coming or going. The relationship would be that of a right triangle, where the speed of light (C) in the absolute frame of reference was the hypotenuse of the triangle, the speed of the ether wind (V) was the far side of the triangle, and the measured speed of light (Cm) was the adjacent side of the triangle. By the Pythagorean theorem:
C^2 = V^2 + Cm^2
This gives the measured speed of light as:
Cm = SQRT( C^2 - V^2 )
-- and the ratio of the measured speed of light to the actual speed of light as:
Cm/C = SQRT( 1 - V^2/C^2 )
= SQRT( 1 - Cf^2 )
-- where Cf is V/C, the velocity expressed as a fraction of the speed of light.
The idea behind the Michelson-Morley apparatus was to observe the interference fringes when the apparatus was in one orientation, and then observe their change when the apparatus was rotated. That would cyclically shift the position of the interference fringes in the eyepiece as per the changes in path length of the light beams in the two arms. The problem was that, when the experiment was actually performed, there was no perceptible shift; Earth didn't seem to have any appreciable speed relative to the ether wind. The speed of light seemed to be the same along both arms of the interferometer, no matter what the orientation of the device was.
There was no perceptible effect between readings 12 hours apart, when the spin of the Earth changed the direction of the interferometer's movement relative to the Earth's orbit; or readings six months apart, when the Earth's movement along its orbit had reversed relative to local space. Refined experiments gave the same results. Something seemed to be wrong, but nobody could figure out exactly what; no matter what was done, the experiment always gave the same result.
* Physicists were baffled. It was suggested that possibly the Earth dragged the ether around with it, but in 1885 the Dutch physicist Hendrik Lorentz (1853:1928) proved that couldn't be the case. In 1889, the Irish physicist George Fitzgerald (1851:1901) suggested that the discrepancy could be accounted for if objects shrank in the direction of their motion, giving light a shorter path. Lorentz independently came up with the same idea, and in 1904 published a set of equations describing the phenomenon in more detail. Physicists didn't find the idea too outrageous: possibly the motion of an object resulted in changes in electrical forces that squeezed an object in on itself.
The idea of length contraction turned out to be completely correct, though the original rationale was off base. Einstein took a different view of the problem, leading to his postulate of the constant velocity of light, and to Special Relativity.
BACK_TO_TOP* Albert Einstein was 26 years old in 1905. He had been educated as a physicist, but he hadn't been able to obtain a satisfactory academic position and was working as a clerk in a Swiss patent office to make ends meet while he played with physics in his free time. That year he published three scientific papers, one on the photoelectric effect, one on Brownian motion, and one on Special Relativity. The first two are of no great importance in this document, though the paper on the photoelectric effect was one of the studies that led to modern quantum physics, and also won Einstein the Nobel Prize for physics in 1921.
The paper on Special Relativity considered a very simple but bewildering postulate and examined its implications. Einstein's postulate, mentioned above, was that the speed of light is an absolute constant, an invariant. Any beam of light from any source, no matter how fast its relative motion, will be measured to have exactly the same velocity of about 300,000,000 meters per second by any observer. That is why the Michelson-Morley experiment gave negative results.
That sounds like an unremarkable thing to say at first, until the implications are considered. Supposed Alice is flying towards Bob on Earth in a starship at half the speed of light, and then fires off a flash bulb. By classical physics, the flash would reach Bob at 1.5 times the speed of light. No, said Einstein, it still comes at Bob at the speed of light, no more or less. Similarly, if Alice's starship is moving away from Bob at half the speed of light, classical physics says that the flash will move toward Bob at half the speed of light -- but according to Einstein, it still comes at Bob at the speed of light. Of course, the speed of the flash as seen from the frame of reference of Alice's starship is the speed of light as well, and Alice sees the flash propagate away from the ship in all directions at that speed.
By classical physics, that's completely absurd. If Alice were riding in the back of a truck at 80 KPH and shot a pebble with a slingshot in the forward direction at a velocity of 50 KPH, then ignoring wind resistance, the pebble's velocity as seen by Bob at the side of the road would be 80+50 = 130 KPH. If Alice shot the pebble in the backward direction, Bob would see it as flying away at 80-50 = 30 KPH.
To emphasize just how crazy an idea this is, suppose Alice flies right by Bob at half the speed of light, and Bob fires off a flash bulb when she passes by. The light flies away from Bob at what he sees as the speed of light in all directions; but it also flies away from Alice at what she sees as the speed of light in all directions, even though she is moving at half the speed of light relative to Bob. That sounds completely illogical.
However, what Einstein pointed out was that it was classical physics that was illogical as far as the propagation of light was concerned. If the speed of light was relative to the motion of a specific frame of reference, there could be a frame of reference where light would stand still or go backwards. If Alice lived in such a frame of reference, she wouldn't be able to see herself in a mirror. Incidentally, Einstein always insisted that it was this line of reasoning that led him to Special Relativity, not the negative results of the Michelson-Morley experiment; he couldn't recollect if he had even heard of the experiment when he started writing the paper.
What Einstein did was extend the concept of Galilean Relativity to the observed behavior of light; Einstein was saying that the symmetry of the laws of motion also applied to light. Galileo observed that there was no way to tell the difference between an object at rest and an object in uniform motion, and according to Einstein that same principle also applied to light. Alice cannot determine if she is in motion or at rest by measuring the speed of light relative to her. The equivalence principle says it will always be the same.
The lack of an ether wind also led to the collapse of the notion of a luminiferous ether. The other branch of modern physics, quantum physics, demonstrated that although light had some properties of a wave, such as wave interference, it also had some properties of a particle, such as the ability to propagate through space without requiring any transmission medium. Light particles are now known as "photons"; they were originally implied by Einstein's 1905 paper on the photoelectric effect. This "wave-particle duality" was something of a bizarre notion in itself, with experiments to prove that light was a wave tending to show that it was a wave, and experiments to prove light was a particle tending to show that it was a particle -- but that's another can of worms that is addressed elsewhere, in a document on quantum physics.
In any case, nobody has ever observed light traveling at any less than 300,000,000 meters per second in a vacuum. One striking example is "synchrotron radiation", which is high-energy electromagnetic radiation being curved around by magnetic fields in a particle accelerator. The particles can be pushed up to significant fractions of the speed of light, but the light they emit still has a velocity of 300,000,000 meters per second by anybody who cares to measure it.
* The principle of the constant velocity of light is as well established as the inverse-square law of gravity. Nobody has figured out a way to make light stop in free space, or even slow it down. As the famous physicist Dick Feynman suggested in another context, anyone who doesn't believe in the constant velocity of light should go do the experiments until he does believe it. Improved versions of the Michelson-Morley experiment have been performed that have established that the speed of light in all directions is constant to within about 1 part in 10^15.
It's true that light will slow down when it travels through a transparent gaseous, liquid, or solid medium, but this is little more than fine print. All that happens is that photons are absorbed by atoms in the medium and then re-emitted, which imposes a delay. When the photons are traveling between atoms in the medium, they're still moving at 300,000,000 meters per second, and Einstein's postulate remains valid.
Not so incidentally, Einstein's postulate that the speed of light was invariant was in a broad sense equivalent to saying that Maxwell's equations of electromagnetism were invariant. Galileo had determined that the laws of motion were invariant; Einstein declared that Maxwell's equations had to be invariant as well, that no matter what the frame of reference was, the equations still worked the same.
* The notion that the speed of light was an absolute constant had a number of counterintuitive implications. The first was that nothing could go faster than the speed of light. Suppose Alice is on a starship and emits a flash of light. By the equivalence principle, it propagates away from Alice at the speed of light in all directions, and obviously precedes her in the direction of her motion. Suppose Bob on Earth sees that flash. The light of the flash has necessarily arrived before Alice has, and since the flash is moving at the speed of light, she must have been moving more slowly than that.
There was another interesting implication: time slows down in a moving object.
BACK_TO_TOP* To see why time slows down in a moving object, suppose that Bob is watching Alice flying across his line of sight in her glass cube. Suppose Alice is carrying in her cube a "clock" consisting of a pair of mirrors oriented at a vertical right angle to Bob's line of sight, with the "ticks" of the clock defined by the time it takes a light pulse to bounce back and forth between the mirrors.
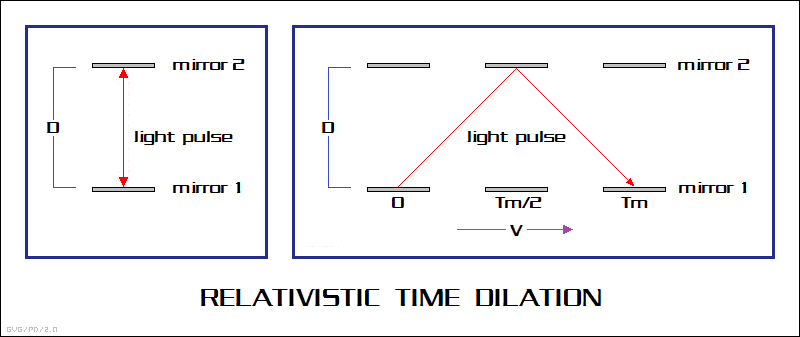
This clock keeps perfect time on the cube. The light pulse moves back and forth between the mirrors at a constant speed, and the distance between the mirrors remains constant as well. If we designate the speed of light as usual by C and the distance between the mirrors as D, then the tick time T is given by:
T = 2 * D / C
However, if Bob is watching the operation of this clock from Earth as Alice's cube flies by, then the mirrors are moving as the pulse flies between them. This makes the path length longer for the light pulse and increases the tick time as measured by Bob.
Let's designate this longer measured time by Tm and the velocity of Alice's cube by V. Then the distance traveled by clock in the time it takes for the pulse to make a one-way trip from one mirror to the other is:
Tm * V / 2
-- and so the round-trip time is:
Tm * V
Since there is no motion in the vertical direction, the vertical distance in both frames of reference must be the same, and so this distance D is given by:
D = T * C / 2
-- and the light must bounce up and down over this separation, meaning that it travels a total distance of:
T * C
Bob's measured tick time Tm is the total distance that light has to travel divided by the speed of light C. By the Pythagorean theorem:
SQRT(( T * C )^2 + ( Tm * V )^2 )
Tm = ---------------------------------
C
Solving algebraically:
Tm^2 * C^2 = ( T * C )^2 + ( Tm * V )^2
Tm^2 * C^2 - Tm^2 * V^2 = T^2 * C^2
Tm^2 * ( C^2 - V^2 ) = T^2 * C^2
T^2 * C^2
Tm^2 = ---------
C^2 - V^2
T^2
= ------------------
( C^2 - V^2) / C^2
T^2
= -----------
1 - V^2/C^2
T^2
= --------
1 - Cf^2
T
Tm = ----------------
SQRT( 1 - Cf^2 )
( 2 * D / C )
= ----------------
SQRT( 1 - Cf^2 )
That means that Bob sees Alice's clock slowing down by the factor:
1 / SQRT( 1 - Cf^2 )
This is the first consequence of Special Relativity: "time dilation". A moving clock slows down. As the velocity of Alice's cube approaches that of light, the clock tick time lengthens toward infinity:
Cf factor _______ ______ 0.1 1.01 0.5 1.15 0.8 1.67 0.9 2.29 0.95 3.20 0.99 7.09 0.999 22.37 0.9999 70.71 0.99999 223.61 _______ ______
If something could reach the speed of light, time would stop. Incidentally, since light of course travels at the speed of light, time does not exist for a photon -- the implication being that a particular photon will never change in any way for the full duration of its existence. In our existence, we see a photon generated by an atom or other particle traveling though space, being reflected to follow a zigzag path until it is finally absorbed again. From the photon's "point of view", it is a thread traced through space along that zigzag path, from what we see as its origin and what we see as its termination, and the question of its duration doesn't have any meaning in that context.
This analysis of time dilation was for a clock moving at a right angle to a path along Bob's line of sight, but it keeps the same time no matter what the clock orientation is. To Bob, the clocks in Alice's cube all run more slowly by the same factor. If they didn't, Alice could turn a clock on its side, leave it to run for a while, and then right it again, and it would have a different time than a second clock that remained upright. That doesn't and can't happen in the frame of reference of Alice's cube, any more than it would happen if Bob had the same sort of clocks in (say) his kitchen, turned one on its side, and later set it back up again.
Before Einstein, physicists had always assumed that time was an absolute. No matter where Alice and Bob were, if they both had accurate clocks, their clocks would keep the same time, and if they went their separate ways, no matter what they did, when they got back together their clocks would still be in agreement. This is, from the point of view of our daily lives, absolutely common sense. It is also wrong -- though it takes moving around at velocities outside of our direct experience to make the effect noticeable.
BACK_TO_TOP* A detailed analysis of the behavior of the clock lying on its side leads to some interesting conclusions, but that analysis is much simpler if we take a digression first.
Suppose Alice is flying in a starship to a star system a distance D away from Earth at a velocity V, and this star system is not moving at any appreciable speed relative to the Earth. The time T it takes the starship to reach the star system is simply:
T = D / V
If the star system is ten light-years away and the starship is moving at half the speed of light, then Alice's journey as seen by Bob on Earth takes 20 years. However, Bob also notices that the starship's clock is running more slowly, and in principle Bob could count all the ticks of Alice's clock from departure from Earth to arrival at the remote star system to prove that in fact time has run more slowly for Alice on the starship -- time dilation is not an optical illusion. That means that Alice has traversed the distance D in a time Tm, which is shorter than T as given by the formula we have already derived:
Tm = T / SQRT( 1 - Cf^2 )
By the equivalence principle, the velocity of the external Universe as seen by Alice on the starship is the same as the velocity of the starship as seen by Bob on Earth. Since the velocity is the same from either point of view but the flight time is shorter, that means that the distance Dm from the Earth to the distant star system as seen by Alice has to be shorter by the same factor:
Dm = D * SQRT( 1 - Cf^2 )
Of course, the equivalence principle also implies that Bob sees the starship (but nothing else) as being shorter in the direction of its motion by this same factor. This is the second consequence of Special Relativity: "length contraction". A moving object becomes shorter in the direction of its motion; at the speed of light, its length would go to zero, another big hint that the speed of light is an absolute barrier. Incidentally, the length contraction equation was not Einstein's invention as such; he inherited it from the preliminary work of Lorentz and Fitzgerald, and so it is often called the "Lorentz-Fitzgerald contraction" or just "Lorentz equation".
* Given the length contraction factor, we can now analyze the behavior of the clock lying on its side in a simple way.
First, we'll make the assumption that the distance D between the mirrors is the same as it is when it's upright, even though this assumption has just been shown to be false. Obviously, when the light beam is moving in the direction of the motion of the clock, the amount of time it takes to move from one mirror to the other will be much longer than it will be when moving against the direction of motion.
We'll designate the time of the forward transit as Tf and the time of the reverse transit as Tr. This means the total tick time is:
T = Tf + Tr
The value of Tf is given by the amount of time light takes to cover the distance between the mirrors, plus the distance the clock travels in that time:
D + V * Tf
Tf = ----------
C
Solving for Tf:
Tf * C = D + V * Tf
Tf * C - V * Tf = D
Tf * ( C - V ) = D
D
Tf = -----
C - V
Similarly, the value of Tr is given by the amount of time light takes to cover the distance between the mirrors, minus the distance the clock travels in that time:
D - V * Tr
Tr = ----------
C
This gives:
D
Tr = -----
C + V
So:
T = Tf + Tr
D D
= ----- + -----
C - V C + V
D * ( C + V ) + D * ( C - V )
= -----------------------------
C^2 - V^2
2 * D * C
= ---------
C^2 - V^2
2 * D * C
= ---------------------
C^2 * ( 1 - V^2/C^2 )
2 * D
= ----------------
C * ( 1 - Cf^2 )
This is not the same result as the upright clock, which is absurd. But if we now factor in the length contraction factor SQRT(1-Cf^2), we get:
2 * D * SQRT( 1 - Cf^2 )
Tm = ------------------------
C * ( 1 - Cf^2 )
2 * D / C
= ----------------
SQRT( 1 - Cf^2 )
-- which is the same as the result above.
This seems a little counterintuitive. If the clock's length is shorter when it is lying on its side, then shouldn't the clock run faster when it's in motion since the light doesn't have as far to travel? However, the trick is that the second mirror of the clock moves away from the first as the light pulse moves forward to catch it, and at high fractions of lightspeed this results in a substantial increase in the distance the light pulse has to travel. To be sure, when the pulse bounces back to the first mirror, the length and trip time is shortened, but not enough to cancel out the increased trip time in the forward direction.
* The previous sections have shown that time and space are not constants. That is a necessary consequence of the fact that the speed of light is a constant. The Michelson-Morley experiment was conducted on the basis that space and time were constants, and so the speed of light had to vary. Einstein turned that logic around, showing that if the speed of light were a constant, then space and time had to vary.
Lorentz and Fitzgerald had taken the first step by asserting that space had to vary; they had taken a major step in the right direction, but the two physicists were too conservative to take the next step and assert, as Einstein did, that time had to vary as well. It was a big step to take. According to the story, Einstein was hammering out his thoughts with Michele Besso, another physicist who had taken a job at the patent office, and then went home to sleep on it. The next day, Einstein came in to work and told Besso: "Thank you! I have completely solved the problem."
There are some extremist critics of Einstein -- a few of them with blatant antisemitic agendas -- who point to his debt to the work of Lorentz and Fitzgerald, as well as the work of the French mathematician and physicist Henri Poincare (1854:1912), who elaborated on the work of Lorentz -- and insist that Einstein was a plagiarist and fraud. However, it is normal that the work of a physicist "stands on the shoulders" of those who came before him. Einstein admitted that special relativity was a comparatively obvious step forward, saying that if he hadn't come up with it, somebody else would have soon enough; in fact, Poincare seemed to have all the pieces, he just failed to assemble them in a persuasive fashion.
There were no serious allegations of plagiarism against Einstein at the time, and in fact in 1927 Lorentz, a highly prominent physicist of the era, acknowledged his failure to understand the relativity of time, and insisted that the credit for relativity belonged to Einstein alone, which was almost being too gracious. The two scientists were on cordial terms; the same wasn't true of Poincare and Einstein, since Poincare pointedly snubbed Einstein's work, and Einstein returned the favor. However, Poincare never made any accusations of plagiarism against Einstein either.
BACK_TO_TOP* Along with time dilation and length contraction, Einstein also realized that a constant speed of light meant that events that were simultaneous in one frame of reference were not necessarily simultaneous in another.
Let's go back to the scenario in which Alice is flying across Bob's line of sight at great velocity in a glass cube. This time, however, let's suppose that as Alice flies by, she lights off a flashbulb positioned in the center of the cube, which sends a light pulse out towards detectors on the front and back of the cube.
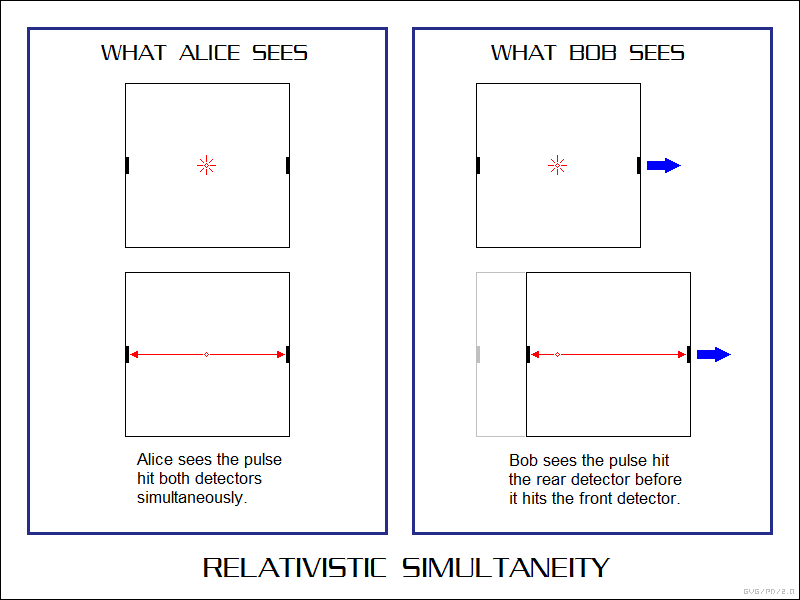
To Alice in the cube, the pulse has to move an equal distance to hit the front and back, and so the pulse hits both detectors simultaneously. To Bob, however, as the pulse moves backward, the back of the cube moves toward it, and as the pulse moves forward, the front of the cube moves away from it. The light from the pulse strikes the detector in the back before it strikes the detector in front. To Alice, the detectors pick up the pulse at the same time. To Bob, the rear detector picks up the pulse before the front detector. If Alice has mounted clocks on the front and rear faces of the cube and synchronized them to her satisfaction, Bob will see the clock on the rear run ahead of the clock in the front.
Of course, Bob will see Alice's cube as length-contracted, but that is of no great importance in this example. Length contraction is linear: the front half of the cube contracts by exactly the same amount as the rear half, and so the middle of the cube stays where it is.
Incidentally, it's obvious from this scenario that no matter how fast Alice is moving relative to Bob, he will see the pulse hit the walls after Alice fires off the flashbulb. One of the implications of Special Relativity is that causality is preserved in all frames of reference: if events with a causal relationship to each other occur in the sequence A-B-C-D in one frame of reference, then they will be observed to happen in the sequence A-B-C-D in every other possible frame of reference. One of the conceptual difficulties with faster-than-light travel is that it implies there will a frame of reference where this causal sequence doesn't hold -- B happens before A -- violating the law of cause and effect. We might be going too far to say that violations of causality are provably impossible, but they certainly defy all experience, and nobody would sensibly bet they're going to happen.
* What Einstein was saying, in short, was that simultaneity is as relative as length and time. Suppose Alice and Bob are working far apart, are motionless to each other, and have clocks that as far as they are concerned are synchronized with each other. Suppose further that they have agreed to each punch a button (or do some other arbitrary action) when their clocks reach exactly noon, and that they are being observed by a third party, who we'll name "Carl".
If Carl is not moving relative to Bob and Alice, when the two of them punch the button, Carl will determine that in his frame of reference they punched the buttons at the same time. If Carl is moving at high speed from Bob towards Alice, he will determine that Alice punched her button first; if he is moving at high speed from Alice towards Bob, he will determine that Bob punched his button first. There is no such thing as absolute simultaneity, which creates difficulties for schemes that propose instantaneous communications.
* This chapter has now provided all the basic pieces for an understanding of Special Relativity. Each of the pieces is more or less counterintuitive, not the way we see the world around us actually working, and they can seem to lead to paradoxes, dead contradictions. However, if the principles are considered together the paradoxes can be resolved, and such matters are discussed in detail in the next chapter.
BACK_TO_TOP