
* This chapter introduces the concept of "spacetime" and then gives a broad description of General Relativity, Einstein's theory of gravity, a subject whose mathematical complexity rules out discussion in detail in this document.
* One thing that is apparent is that Special Relativity's modifications to traditional concepts of space and time are not arbitrary. They follow specific rules and have to add up according to them. Under these rules, the three spatial dimensions are modified in a way that interacts with modifications in time. This was demonstrated in the discussions of relativistic paradoxes in previous chapters. For example, in the Twin Paradox Alice sees a compression of space that is compensated for by a matching expansion -- dilation -- of time. If time or space are considered separately in the two cases of Alice and Bob, the results seem contradictory, but if the space and time seen by Alice and Bob are properly summed, then the result is the same, "invariant", for both of them.
Put another way, Special Relativity deals with the properties of four-dimensional "spacetime", while classical physics deals with three-dimensional space and time as independent physical properties. It was Minkowski who suggested the notion of spacetime, introducing the Minkowski diagrams shown previously, in a lecture delivered in 1908 and published in 1909 shortly after his death. The idea had certainly been implicit in Einstein's 1905 paper, but Einstein had taken a more strictly mathematical approach.
At first, Einstein had little interest in Minkowski's spacetime concept and graphical analysis, feeling that it was just cluttering up his equations. Einstein hadn't hit it off well with his university instructors, and in fact Minkowski described Einstein as a "lazy dog", though it appears that Einstein was merely selective, focusing on matters that seemed relevant to him while being impatient with the rigid coursework. To pass his finals, Einstein had to lean heavily on the tutoring of a more mathematically-inclined friend, Marcel Grossman.
Einstein on his part ended up with some hard feelings about his university experience, partly because since childhood he had been inclined to question the conventional wisdom of things, and so the generally dogmatic approach of a university education rubbed him the wrong way. He also had a specific reason for his negative attitude: his academic supervisor, Heinrich Weber, would not recommend Einstein to potential employers, which is why Einstein ended up taking a job as a patent clerk. (Some sources claim that it was Grossman who got Einstein the job.) However, Einstein would eventually come around to Minkowski's point of view about spacetime.
In any case, spacetime is a concept that can be and often is belabored because it sounds mysterious. It isn't. Anyone can build a spacetime diagram for a road trip: mark hours on the horizontal axis, kilometers on the vertical axis, and then draw a line of the number of kilometers traversed as the hours pass. The idea, in itself, is trivial, and as noted above, Einstein originally wasn't much interested in it. What interested him about it was the fact that, although time had no dependency on space in traditional physics, it did in his refined physics.
BACK_TO_TOP* Spacetime was still not all that essential to Einstein's development of Special Relativity -- but then he started to consider folding gravity into his relativistic framework. Special Relativity ignores the effects of gravity, and that means that the Earth or any other object with an appreciable mass and gravitational effect can only be considered a frame of reference by ignoring gravity and simply assuming everything is glued to its surface.
That was unsatisfactory, and so in 1907, Einstein began to focus on fixing the omission of gravity. The first thing he did was extend his relativistic equivalence principle to scenarios in which gravity is involved. Suppose Alice is in a cube with no windows, drifting in free space, weightlessly floating around inside the cube. Suppose, however, Alice's cube is being pulled down from space by the force of gravity towards the surface of a planet. Since she is being accelerated at the same rate as the cube, she will still be floating around weightlessly and will have no perception that she is moving. She will be in "free fall".
In broader terms, Alice will observe exactly the same physical laws inside her cube, no matter if it is floating free or being drawn down in a gravitational field. On the other side of the coin, if Alice's windowless cube is being accelerated through free space at 9.81 meters per second, everything will appear to her just as if the cube were sitting motionless on the surface of the Earth.
Einstein saw the scenario in more commonplace terms, thinking of someone falling off of a roof. One of the first implications that Einstein pulled from this concept was that time would slow down in a gravity field. Suppose Bob is at the front of a long spaceship and Alice is at the rear. Suppose further that they send light pulses to each other every second, by their own individual clocks. If the spaceship is not accelerating, Bob will receive one pulse from Alice every second and Alice will receive one pulse from Bob every second.
However, if the spaceship is accelerating, say at 9.81 meters per second per second, Bob will receive Alice's light pulse on an interval longer than one second, and Alice will receive Bob's light pulse on an interval shorter than one second. By the equivalence principle, there is no way to distinguish between this situation and the long spaceship sitting on the Earth, in a gravity field with an acceleration of 9.81 meters per second per second. Alice's clock runs slower than Bob's. One of the implications of this is that light would also be "redshifted" coming out of a gravity well, just as if it were undergoing a Doppler shift after being emitted by a source moving away from an observer.
In addition, the equivalence principle shed some light on one of the subtle puzzles of physics: the equivalence of "inertial" mass and "gravitational" mass. Mass is defined in classical physics as the ratio of force to acceleration of an object:
force
mass = ------------
acceleration
Mass is also the source of gravitational force (GF):
constant * mass1 * mass2
GF = ------------------------
distance^2
Now contrast gravitational force with electrostatic force (EF), which is defined as:
constant * charge1 * charge2
EF = ----------------------------
distance^2
An electrostatic force only depends on a charge imbalance, and has nothing to do with the mass of the objects carrying the charges. However, the acceleration of the objects under an electrostatic force still depends on the mass. With gravity, in contrast, both the (gravitational) force and the acceleration depend on the mass. According to Einstein, this was absolutely no coincidence; it was what was to be expected if acceleration of a mass could not be distinguished from gravity acting on the mass.
Einstein dropped the matter for the moment. When Minkowski came up with the notion of spacetime, Einstein rejected it, though he would have second thoughts later.
* There is a popular belief that "they thought Einstein was crazy". In fact, though his 1905 papers did create some controversy, they were so obviously well-thought-out and original that they catapulted him, within a few years, from obscurity to the top rank of contemporary physicists, likely somewhat to the shock of some of his university professors. His paper on relativity, incidentally, was nowhere near as controversial or as radical as his paper on the photoelectric effect, since it implied that light acted as a particle -- what would later be called the photon -- and not as a wave, which by most of the evidence it seemed to be. Even Einstein admitted to being baffled by his own idea; when the American experimental physicist Robert Millikan (1868:1953) tried to disprove the notion, his thorough experiments forced him to admit it was correct despite its "unreasonableness".
In any case, Einstein's work had made him famous. He stayed at the patent office until 1909, finding the pay reasonable and the work pleasant, though increasingly physicists wondered what he was doing there. He finally got a position at the University of Berlin, which was a good thing of course, but now he had to deal with the overhead of being a university professor -- writing lectures and delivering them, dealing with students and administration, and so on. He found the overhead tedious, but at the time pure research positions were unusual, possibly unheard of.
Einstein came back to the problem of relativistic gravity in 1911. In his earlier work on the subject, he had ignored the issue of tidal forces. Tidal forces arise because gravity falls off with distance, and so there is a differential gravitational force on an extended object that sets up a stress in it from front to back, and also tends to squeeze it in towards the middle.
Einstein had previously assumed gravity worked on all parts of an object in its field uniformly. That is close enough to the truth for Alice in a cube in the gravity field of a normal planet, but not true at all for a very large object in the gravity field of a planet, or for a small object like Alice's cube in a close vicinity of a huge, very dense mass. If Alice were in her windowless cube and was being pulled towards such a mass, she could tell she was actually in a gravity field because she would be stretched and squeezed, warning her to quickly get her cube out of the potentially deadly fall towards the object.
How could this be reconciled with the equivalence principle? Einstein spent about a year tinkering with the notion that it was the variation or "warpage" of time in a gravitational field that could take care of the tidal issue, but in 1912 he decided, probably a little sheepishly, that Minkowski had been right about the idea of spacetime after all. Einstein worked out that a warpage of spacetime could deal with the matter of tides, or in more general terms that gravity was actually a warpage of spacetime caused by a mass.
Suppose Alice and Bob are in their cubes and have been flying unpowered through deep space a good distance apart, with no relative motion; during their flight, they follow precisely parallel lines. Suppose, then, that they come up on a planet, with Bob flying along a line that would take him along one side of the planet, and Alice flying along a line that would take her along the other side of the planet. What happens then is that they both are pulled toward the planet, and their paths begin to converge. According to Einstein, the flight of Alice and Bob is continuing on path, it's just that the spacetime path has been distorted by the mass to bring the two paths closer together. They are following the shortest path or "geodesic" through spacetime. Tidal effects become noticeable when the spacetime curvature is large relative to the object in question.
Of course, the equivalence principle meant that accelerations were also associated with spacetime curvature. Consider the traditional carnival ride usually known as the "Tornado". Alice gets into a big drum that is then set to spinning, plastering her up against the wall of the drum, and then the floor drops out from below her, leaving her pinned to the wall. According to Special Relativity, the length of a moving object shrinks in the direction of its motion, and so Bob, who is watching Alice ride the Tornado from the outside, sees that the circumference of the walls shrinks (and incidentally sees Alice's watch slow down). However, he doesn't see the diameter of the Tornado shrink -- the ride may be spinning, but there is no motion in the across the plane of his rotation -- and so the relationship between the diameter and the circumference of the ride is less than PI.
Objects being spun in a circle will fly off in a straight line if released, but they are always being pulled back to the center of the circle. According to Einstein, this "radial acceleration" will result in spacetime curvature, which is what Bob observes.
* That was a revelation, but Einstein's intuition wasn't enough, he had to be able to "do the math". He didn't have a precise idea of where to start, so he contacted his friend Marcel Grossman, now a professor of mathematics, who scratched his head for a bit and found what Einstein was looking for. It was a mathematical system known as "tensor calculus", referred to in modern times as "differential analysis". Grossman told Einstein it was nasty, too nasty for a physicist to want to tinker with, but Einstein knew there wasn't anything else that would do the job. Einstein struggled with it, pleading with Grossman for assistance: "You must help me or I will go mad." Grossman came to his assistance, and in 1915 Einstein announced the result, his theory of General Relativity, to the world -- though it wouldn't really receive much attention for a few years, being upstaged by the First World War.
Incidentally, as with special relativity, there are critics who insist that Einstein plagiarized general relativity, since it had a heavy though acknowledged debt to Grossman, and the mathematician David Hilbert (1862:1943) was working on similar concepts in parallel. Once again, there was no outcry about plagiarism at the time, and the accusations seem to be no more than contrived accusations after the fact.
* In most elementary discussions of General Relativity, the analogy is made with a rubber sheet on which heavy balls are placed. The balls sink into the sheet, distorting it in a way analogous to the way masses reside in a distortion of spacetime in their vicinity. It is important to remember that this distortion is not caused by gravity; it is gravity. The paths of objects moving across the sheet will curve along with the distortions.
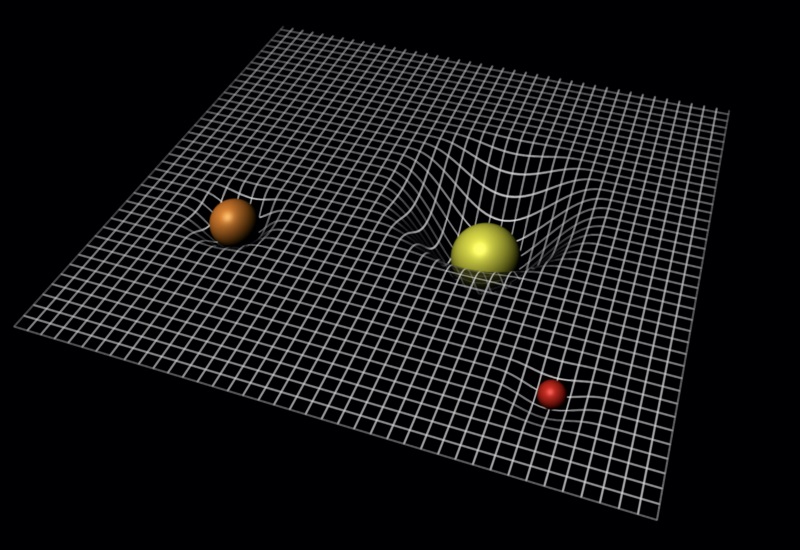
In fact, light itself will follow curved paths through this distorted spacetime. This also demonstrated the equivalence with accelerated motion, since a light beam flashed across an accelerating starship would curve across the starship's direction of motion. Other clauses of General Relativity state that, as described above, clocks will slow down in a gravitational field and that light will be redshifted coming out of a strong gravitational field.
General Relativity's analysis of the behavior of gravity differs from that of Newton's classical theory in a few subtle respects. General Relativity was used to account for small discrepancies in the orbit of Mercury that could not be explained by classical theory, and was one of the first proofs of the concept.
The bending of starlight predicted by General Relativity was also confirmed during an eclipse of the Sun in 1919 -- though later analysis of the photographs taken showed the errors in the measurements were of the same magnitude as the effect being measured. Uncertainties in the observations didn't matter too much even then, since physicists found General Relativity persuasive on the elegance of the argument itself and were confident that it would be validated. More reliable estimates eventually proved the predictions of General Relativity. The bending of the images of distant galaxies around large intermediate galaxies to create "double" images is very well established in the present day, and in fact has been used as a tool in deep-space surveys.
As with Special Relativity, lab experiments have also confirmed the validity of General Relativity. In 1976, an atomic clock was launched on a sounding rocket to an altitude of 1,000 kilometers, and its timing ran slow compared to an earthbound twin at the rate expected by General Relativity. In experiments conducted by the US National Institute of Standards & Technology (NIST), a precision clock was raised 33 centimeters (about a foot) and measured to be running slower by a rate of about a 90-billionth of a second in 79 years. Incidentally, in another part of the experiment, an aluminum ion being used as a clocking element was put into cyclical motion using an electric field, with the "clock" becoming slower once it was in motion, as predicted by Special Relativity.
General Relativity also leads to a few predictions that could not have been considered with classical theory. Before Einstein, the general assumption had been that the effects of gravity between two objects were instantaneous no matter how distant the two objects were, and one of Einstein's motivations in extending relativity to cover gravity was to get rid of this assumption, since he knew that nothing could exceed the speed of light.
Under General Relativity, the effects of gravity propagate through the Universe at the speed of light. In particular, the collapse of massive objects, or massive objects in tight orbits around each other, could set up a distortion of spacetime that propagates through the Universe as a "gravity wave". Observations of the orbits of pairs of ultradense stellar fossils known as "neutron stars" -- each with a mass on the order of that of the Sun, but the size of a mountain -- show the pairs are falling together at a rate consistent with the loss of energy by gravitational radiation as predicted by General Relativity. Work on detector systems to directly observe gravitational waves proceeded in a slow fashion over the past few decades, but the gravitational waves were finally observed in 2015, and such observations are now routine.
* The description of General Relativity given above gives a highly simplified view of an extremely difficult theory, one which Einstein himself said made Special Relativity look like "child's play". Sir Arthur Stanley Eddington (1882:1944), a prominent physicist who was a pioneer in understanding stellar evolution and one of General Relativity's early backers, was asked once by a reporter if it were true that only three people in the world understood the theory. Eddington simply stared off into space in an abstracted fashion. When asked what the trouble was, he replied: "I'm trying to think of who the third person might be."
BACK_TO_TOP* Another prediction of General Relativity is that if a massive object becomes sufficiently dense, spacetime will curve around it and light will no longer be able to escape from it. The object would become a "black hole" in space, the mass collapsing in on itself forever to form a "singularity". Such objects could result from the explosive collapse of very large stars. Einstein himself was reluctant to believe that they were possible, even writing a paper in 1939 trying to disprove their existence, claiming that the formation of such an object would require that the particles of the mass forming it exceed the speed of light.

Then, during the 1960s, neutron stars were discovered by radio telescopes. Neutron stars had also been generally regarded as impossible, and their discovery allowed the theoreticians to take a closer look at the physics of black holes, determining that they were more sensible than had been generally assumed to that time. Since then, a number of star systems have been discovered where one of the stars is so massive and compact that nobody can figure out what else they could be except black holes. Supermassive black holes with the mass of millions or even hundreds of millions of Suns are believed to commonly reside at the center of galaxies.
Some physicists have come up with alternate models that avoid the formation of a singularity; one interesting one points to the slight energy inherent in the vacuum of space itself and postulates that the accumulation of that energy in the collapse of a mass will build up a "degeneracy pressure" that halts the collapse, resulting in a "black star" instead of a "black hole". However, at present this is a minority view that most physicists tend to find contrived, a dodge to get around an uncomfortable idea. To be sure, absolutely proving that black holes exist is very difficult, since they emit no light and cannot be observed directly, but for the time being the existence of black holes is generally accepted.
If black holes do exist, their properties are very interesting. Suppose Alice sends a robot named Robby on a spaceship to investigate a black hole. As he descends deeper into the gravity well of the black hole, his clock will slow down compared to Alice's clock, and any light emitted by his ship will be increasingly redshifted. He will also suffer from increasing tidal forces that will threaten to rip him from head to foot; these tidal forces will be more pronounced for a small black hole than a large one, since the gravitational gradient is steeper for a small hole than a big one.
At a certain critical distance from the center of the black hole, light will no longer be able to escape, and so if Robby the robot goes below that critical distance, neither will he. This critical distance is known as the "Schwarzchild radius" -- after the physicist Karl Schwarzchild (1873:1916), who came up with the notion of a black hole in 1915 -- and the "surface" defined by this radius is known as the "event horizon". Once Robby falls below the event horizon, there is no way for him to escape or even communicate with the rest of the Universe, since any signals he tries to send back up will not be able to get out of the plummeting gravity well. As far as Alice was concerned, poor Robby disappeared from view, and will never re-emerge.
Since big stars or other cosmic objects that form black holes are always rotating, the black holes that result from them will rotate as well. This might seem like a non-issue since a black hole is featureless, but its rotation will not only make the hole itself an ellipsoid instead of a perfect sphere, it will drag spacetime outside of the event horizon around with it, forcing rotation on any object as it falls in. This rotating space stores a tremendous amount of energy, and some researchers have envisioned ways of extracting that energy, either to show how energetic cosmic objects are powered, or to play with ideas for "dream machines" achievable by some civilization with technical capabilities far beyond our own.
It may be possible to actually create ultra-tiny black holes using high-energy particle accelerators. That might sound incredibly dangerous, presenting the possibility that the tiny black hole might simply grow continuously until it swallowed up the entire Earth, but modern considerations of quantum physics show that black holes leak mass, and they will eventually evaporate. For a black hole the mass of a star, the leakage rate is so low that the time it takes for the hole to evaporate is vastly longer than the age of the Universe, but an ultrasmall black hole will evaporate almost instantly -- so quickly as to make it hard to detect.
The objection may be raised that theory might be wrong -- and in fact, when a physics lab proposed to create miniholes, a protest was submitted to a court of law to block the effort. The case was thrown out: if it is possible to create tiny black holes in a particle accelerator, they are also being created continuously by the impact of high energy space particles, the "cosmic rays", on the Earth's upper atmosphere. The Earth is still here.
Incidentally, as mentioned in the previous chapter, there are some dodgy aspects to the notion of relativistic mass, and one of these aspects can be seen by considering the question: if an object moves rapidly enough, will it become a black hole?
The answer is NO. After all, if Alice is flying ever closer to the speed of light, the mass of everything in the Universe will be increasing from her point of view, which would imply that everything would fall into a black hole. The motion of the object of course is relative, which means that in some frames of reference, the object does not have enough mass to form a black hole, and in others it does. A black hole, in reality, exists in any frame of reference. Obviously, relativistic mass doesn't work quite the same way as invariant mass.
* If Robby survived long enough to reach the event horizon, he won't survive much longer, since the tidal forces inside the event horizon not only keep on growing, they shift back and forth, twisting poor Robby apart as if he were in a huge carnival taffy-pulling machine. He will never reach the singularity at the heart of the black hole intact, and in fact this singularity remains poorly understood. It's not just an issue of the forces and spacetime distortion shooting up towards infinity, making calculations impossible; it's also an issue of the collapse of the singularity to a size in the domain of quantum physics. Attempts to get relativistic physics and quantum physics to play nice with each other have proven troublesome.
In any case, the behavior of singularities remains mysterious. Some physicists have wondered if it is possible for a singularity to re-emerge in a separate part of the Universe with an outpouring of energy as a "white hole", having formed a bridge or "wormhole" through higher-dimensional space between the place where the singularity was created and where it emerges.
The idea goes back to a 1935 paper by Einstein and his assistant Nathan Rosen (1909:1995) in which they tried, unsuccessfully, to model elementary particles as wormholes, or "bridges" in spacetime. In 1963, a New Zealand physicist named Roy Kerr (born 1934) was working on the physics of black holes, and showed that if it were spinning, it could in fact act as a wormhole. The only problem was that nobody could figure out any way of entering into the "Kerr black hole" and getting back out again.
Physicists have continued to investigate the idea, however. The concept of wormholes seems to open the possibility of journeying to distant parts of the cosmos at faster-than-light speeds and even of traveling backward in time, at least up to the moment when a wormhole was created. Science-fiction writers have picked up the notion of wormholes and made extensive use of it, but it is important to realize that wormholes are simply something that, at best, might exist; there is no reason to believe that they must exist.
Wormholes may only exist at the subatomic quantum level and have lifetimes too short to make them directly detectable. Many physicists investigating them do so with the expectation of finding them impossible. In a comment on a movie in which wormholes are used to support an interstellar expedition, popular science figure Neil deGrasse Tyson sent out a message: "They explore a planet near a black hole. Personally, I'd stay as far the hell away from black holes as I can."
* Although Einstein never really accepted black holes as an implication of General Relativity, he did perform pioneering studies of the theory's implications for the Universe as a whole. The mass in the Universe of course has an influence on the geometry of spacetime for the entire Universe. His calculations showed that the Universe couldn't be static: it had to be either expanding or contracting. He thought there was something wrong with his work and introduced an arbitrary "cosmological constant" to make things sit still.
The joke was on him, because in a few decades it was determined that the Universe was indeed in change -- more specifically, it was expanding. Einstein eventually judged his cosmological constant his "biggest blunder". Modern cosmologists suspect he actually wasn't completely wrong, but that's another story.
Many articles are written these days with titles like "Was Einstein Wrong?" Critics of Einstein have a tendency to think that such articles claim scientists are now proving that concepts such as time dilation, length contraction, and the twin paradox really are the nonsense they seem to be at first sight. Actually reading such articles shows all these notions remain perfectly valid and generally accepted; the articles simply suggest that nature may deviate from Einstein's rules at the extremes -- indeed, although physicists haven't yet gone to extremes that have led to deviations, they have little doubt that eventually they will -- and that the overall architecture of the Universe may not be quite what Einstein suggested it would be.
It would be just as valid for authors of the past to write "Was Newton Wrong?" in response to Einstein's discoveries in relativity. Technically yes, Einstein's general relativity is a more accurate description of reality than Newton's theory of gravity. In practice, Newton's theory of gravity is still taught to every student of physics, and it's used to perform such exacting calculations as plotting the trajectories of space probes. The additional fine print and wider scope of general relativity are not usually needed for such calculations. Similarly, any adjustments to Einstein's work will not throw out his discoveries as completely wrong; they will simply add more fine print.
BACK_TO_TOP* Einstein acquired a towering reputation as one of the greatest scientific minds in history. One of the consequences of his fame was that he has become a target of critics in the form of a clique of "Einstein bashers" who are fond of creating websites to show where he went wrong. Some Einstein-basher websites are blatantly antisemitic, but they're a minority: much more often, the website author simply wants to establish that he -- few if any Einstein bashers are female -- is smarter than the great Einstein.
The general message is that the author, predictably a physics amateur, asserts that he has proven Einstein's work is completely broken. The arguments that follow fall into two categories:
In slight mitigation, the mistaken notions of the Einstein bashers do occasionally have roots in the confusing explanations of relativistic physics found in some elementary physics texts. Unfortunately, that isn't enough of an excuse. Even though they generally admit that they do not have professional qualifications in physics -- that is, their knowledge is superficial on the face of it -- they assume they have seen a blatantly obvious fault in Einstein's thinking that professional physicists have cluelessly failed to notice for a century, and remain absolutely oblivious to the fact that their objections, if they actually make any sense to begin with, have long-established answers.
Some actually go ever farther in their determination to bash Einstein, claiming for various incoherent reasons that his work is immoral, a subversive plot of some sort. One might as well conclude that since Newton's law of gravity says that things fall downward, then Newton was saying we all should go jump off a bridge. They will often conclude that Einstein has now been generally abandoned by the scientific community -- a claim that would come as a considerable surprise to the vast majority of physicists.
* There isn't any basic dispute over relativistic physics any longer, but that doesn't mean everyone's comfortable with the idea, either. There's a popular joke, attributed to comedian Steven Wright, which goes: "If you were driving at the speed of light ... and you turned on your headlights ... would you see anything?"
Wright clearly had no idea that precisely this joke had already been invented and answered by Einstein; and if he did and asked for details, the only sensible response would be: "You don't want to know." Most people don't. The math for relativity isn't complicated, at least not for Special Relativity, but it requires a grasp of different ways of thinking. Studying relativity leads to the suspicion that it's trickery, but the logic hangs together, and in fact it's the classical view of things that has the illogical features that can't be resolved.
This document only traces a path through the forest. Playing with the large number of puzzle problems available in formal texts on the subject would likely give those sufficiently interested a better conceptual grasp of the matter, and I suspect eventually that a fair number of computer videos illustrating the appearance of the Universe near lightspeed would help the rest of us who are somewhat lazier.
However, although relativity is logical, it still reminds me of an old Warner Brothers Looney Toons cartoon in which Foghorn Leghorn, a loudmouthed rooster, is trying to play with a kid chicken who would really rather be studying mathematics and physics. As best I recall it, Foghorn persuades the kid to play hide-and-go-seek, and while the kid is counting, Foghorn sneaks through the barnyard and hides in a bin. "Heh!Heh!Heh! He'll nevah find me in hyar!"
The kid finishes counting, does some computations on a piece of paper, walks out to the middle of the barnyard, checks his calculations, draws a cross on the ground, goes and brings back a shovel, pushes it in the ground, leverages it and ... POP! Foghorn appears out of the ground on the shovel blade, sputtering: "WHO?! WHAT?! WHERE?! WHEN?! HOW?! WHY?!" The kid shows him the calculations and Foghorn backs up, waving his hands. (In cartoons, chickens have hands.) Foghorn goes over to the bin and puts his hand on the lid, then says: "Nah, bettah not check. Ah might actually still BE in thar!"
* I wrote this document as a follow-on to an earlier document on interstellar flight. That document took a dim view of the prospects of faster-than-light flight, and I felt I needed to document relativity a bit better to back that position up.
I actually didn't do more than skim a few sources to write the bulk of this document. I originally tried to understand relativity back when I was about 20 or so in the early 1970s. I didn't really understand much then, except for the vital principle of the absolute velocity of light, from which all else flows. I went back to it in the mid-1980s and created a set of hand-written notes. They were taken very directly from the textbook I was using, and though I did acquire an understanding of time dilation, for the other parts I only managed to get a grasp of the mechanics of the math.
The third pass gave me what I believed to be a reasonable basic understanding of the essential elements of special relativity. It was a terrible headache to write, however. The initial editions had a few sections that I looked at later, and had to conclude were so muddled I had to say to myself: "What was I THINKING?!" I deleted them in v1.2.
After that, the document seemed stable until I ran into the works of the Einstein bashers. Although they had no value in themselves, they got me thinking about puzzles in relativistic physics, and I couldn't stop. After a month, I wrote a new revision to reflect major new insights -- not just on how things work but on how to explain how they work, which is a challenge in itself -- and doing the same thing again a month after that. I could have hardly imagined acquiring any comprehension of such things when I started down this path in the early 1970s. I couldn't imagine the headaches I would get, either.
As far as the comments on General Relativity in this document go, I doubt that I will ever expand on them much. I think I've learned as much about it as I'm going to. It matters not; while it is often said that laypersons cannot understand General Relativity, they can understand it perfectly well -- at a layperson's appropriate level of detail. What more do they need to know? It's of no practical use to them.
Incidentally, when I found out in working on the v1.5.0 version of this document that modern physicists have problems with the notion of relativistic mass, preferring to use relativistic momentum, I felt a twinge of despair. Did I need to go back and rewrite everything? Fortunately, at the same time I ran across Stephen Hawking's A BRIEFER HISTORY OF TIME, and to my relief, I found that Hawking used the concept of relativistic mass without bothering with any fine print. Clearly, he understood the technical writer's basic principle that a workable simplification is generally more useful than the complete painful truth. Dick Feynman's classic LECTURES ON PHYSICS also makes no bones about using relativistic mass. If it was good enough for them, it's well more than good enough for me, as long as I've provided the appropriate caveats.
* Formal sources include:
As for illustrations:
All the drawings in the text are my own work.
* Revision history:
v1.0 / 01 jul 99 v1.1 / 01 aug 99 / Tidying and refinements. v1.2 / 01 jan 01 / Cut out a few muddled sections. v1.0.3 / 01 may 02 / Minor update. v1.1.0 / 01 oct 03 / Cleanup, comments on relativistic simultaneity. v1.1.1 / 01 nov 03 / Relativistic simultaneity & twin paradox. v1.2.0 / 01 dec 03 / Considerable update of twin paradox section. v1.3.0 / 01 jul 04 / Cleanup, added summary, historical details. v1.4.0 / 01 mar 05 / More General Relativity, went to 3 chapters. v1.4.1 / 01 may 05 / Minor corrections. v1.5.0 / 01 dec 05 / E=MC2 derivation, went to 4 chapters. v1.5.1 / 01 jan 06 / Relativistic perspective, minor tweaks. v1.5.2 / 01 apr 06 / Very minor tweaks. v1.6.0 / 01 nov 06 / Simplified 3-way paradox, minor tweaks. v1.6.1 / 01 apr 07 / Follow-up polishing release. v1.6.2 / 01 sep 08 / Very minor tweaks. v1.7.0 / 01 feb 10 / Fix on MM experiment, Einstein basher section. v1.7.1 / 01 mar 10 / Follow-up fixes to v1.7.0. v1.7.2 / 01 jun 11 / Review & polish. v1.8.0 / 01 mar 12 / Clean up major bugs in relativistic paradoxes. v1.8.1 / 01 dec 13 / Review & polish. v1.9.0 / 01 oct 15 / General housecleaning. v1.9.1 / 01 sep 17 / General housecleaning. v1.9.2 / 01 aug 19 / Review & polish. v2.0.0 / 01 jul 21 / Review & polish. v2.0.1 / 01 mar 23 / Review & polish.BACK_TO_TOP
