
* One of the simplest, and most difficult to grasp, facets of elementary physics is that of "heat", and that is the starting point for the study of "thermal physics" or "thermophysics". This chapter provides an introduction to thermal physics.
* "Heat" and "temperature" may seem to be intuitive concepts, and certainly we do understand them intuitively from daily experience. We can go outside and notice if the temperature is high on a hot day, or low on a cold one. We put food in the microwave or in the oven to heat it up, and we put icecubes in a drink to cool it down. However, properly defining these terms is tricky. Formally speaking, heat is not a property of an object, but is instead a transfer of energy between objects. It follows a few simple rules:
The great French chemist Antoine Lavoisier (1743:1794) postulated that a hot object contained a concentrated amount of a hypothetical "fluid" that he called "caloric" that was the agent of heat transfer. It could be generated by friction, for example rubbing sticks together to start a fire, and could be converted back into mechanical work, for example using a steam engine.
The idea seems a bit silly in hindsight, but the notion of "imponderable fluids" was popular at the time, and considering electricity as a fluid, as was the case in that era, was not so ridiculous, since an electric current can be thought of as the flow of a "fluid" of electrons. However, the problem with caloric was that its only identifiable characteristic was that it transferred heat. It was not visible in any way, and had no other recognizable properties. What transferred heat? Caloric. What was caloric? It was what transferred heat, no other properties being described. Scholars felt they weren't on very solid ground.
It wasn't long after Lavoisier introduced the idea of caloric that scientists began to understand that heat was simply the consequence of the motion of the molecules in an object -- "molecules" in the broad sense, including individual atoms. Benjamin Thompson (1753:1814) was a Loyalist who backed the wrong side in the American Revolution and had to flee to Europe, where he acquired the title of "Count Rumford". Thompson was working in the arsenal at Munich, and noticed that boring out a cannon generated a good deal of heat. That wasn't any new observation, but he observed that the rate of heating didn't depend at all on the rate at which the cannon bore was ground out, only on how much work was put into the grinding process. A dull tool that ground the bore slowly generated about as much heat at any one time as a sharp tool that ground quickly, if both tools were rotated as fast. From the point of view of caloric theory, the sharp tool that ground quickly should extract more caloric and should release more heat. That wasn't the case, and Thompson realized that he could make the tool duller and duller until he could get heat out of the process indefinitely. That would imply that the cannon blank stored a infinite supply of caloric.
Thompson deduced that the work of the grinding process was being converted into heat, and that caloric was just a fantasy. It would take time for his ideas to be widely accepted, since his writings on the subject were general in nature and not backed up by detailed studies. Others would take up his ideas and put them on a stronger foundation.
James Prescott Joule conducted a series of elegant experiments to demonstrate the link between work and heat, culminating in an 1845 paper in which he described an apparatus in which weights were connected to a cord and a pulley arrangement, to spin a set of paddles in a closed vessel full of water. Using a sensitive thermometer to measure the heat produced by the paddles showed it was predictably proportional to the energy released in the fall of the weight.

It is now known that force generated by friction over time exerts work that produces heat energy, in a cannon or anything else that is affected by friction forces. In more modern terms, adding energy to an object -- by friction or another heating process -- increases the velocity and the kinetic energy of the molecules, increasing the "internal energy" or, more informally, the "thermal energy" of the object. The temperature of the object was then a measure of the thermal energy, essentially an average of the kinetic energy of all the molecules of that object.
Heat in turn became a transfer of this thermal energy. If a hot object were brought in contact with a cooler object, collisions between the energetic molecules of the hot object increased the velocity of the slower molecules of the cooler object. One of the interesting implications of the view of temperature as a measure of molecular motion was that if all molecular motion in an object ceased, then there would be no way for the object to get any colder. This implied the existence of an "absolute zero" temperature.
* There are several different temperature scales in use today. The "Celsius" scale, once known as the "Centigrade" scale, is in use over most of the world, while the "Fahrenheit" scale is used in the United States. The "Kelvin" scale, which is closely related to the Celsius scale, is in common use for scientific purposes.
In the Celsius scale, the freezing point of water is specified as 0 degrees Celsius, while the boiling point is specified as 100 degrees Celsius. In the Fahrenheit scale, the freezing point of water is 32 degrees Fahrenheit and the boiling point is 212 degrees Fahrenheit. Conversions between the two can be performed as follows:
degrees_Fahrenheit = ( 9/5 ) * degrees_Celsius + 32 degrees_Celsius = ( 5/9 ) * ( degrees_Fahrenheit - 32 )
The Kelvin scale is the same as the Celsius scale, except that the 0 point is at absolute zero, which is equivalent to -273.15 degrees Celsius. This makes conversion between the Kelvin and Celsius scales simple:
degrees_Kelvin = degrees_Celsius + 273.15 degrees_Celsius = degrees_Kelvin - 273.15
The Celsius and Fahrenheit scales are useful for describing temperatures in our daily environment, since they give small values for most Earthly temperature ranges. The Kelvin scale is much more convenient for scientific work, since it eliminates negative temperature values that are clumsy in calculations. Incidentally, there is also an (obsolete) "Rankine" scale that is the same as the Fahrenheit scale, except that the 0 point is at absolute zero, equivalent to -459.67 degrees Fahrenheit.
* In metric units, heat and thermal energy are given in terms of the "calorie", which is the amount of heat required to raise a gram of water from 15 degrees Celsius to 16 degrees Celsius at a pressure of one atmosphere. Since heat is equivalent to energy, one calorie is also the same as 4.186 joules. Since the calorie is a somewhat small unit for most practical purposes, it is often expressed in terms of "kilocalories", and just to confuse matters, the "Calorie" used to rate food energy actually means a kilocalorie.
In English units, heat is given by the "British thermal unit (BTU)", which is the amount of heat required to raise a pound of water one degree Fahrenheit. The BTU has been generally obsoleted by the calorie. One BTU is equivalent to 252 calories or 1,055 joules.
BACK_TO_TOP* Heat of course has a number of effects on matter, most visibly on gases. An "ideal gas", meaning one where the molecules that are visualized as generalized perfectly elastic particles that have no tendency to attract each other, has a neat relationship between temperature, volume, and pressure. This can be summarized as the "combined gas law (CGL)":
_________________________________________________________________________
pressure1 * volume1 pressure2 * volume2
--------------------- = ---------------------
temperature1 temperature2
_________________________________________________________________________
For example, suppose Dexter, a junior mad scientist, stores a gas in a rigid airtight container with solid walls -- meaning its volume is constant -- and that the temperature of this gas is the same as the ambient temperature of the outside world. If Dexter then heats up the gas inside the container to twice its original temperature (using the absolute Kelvin scale), then the final pressure is twice the original pressure. Similarly, if Dexter cools the container to half its original temperature, the pressure falls to half of its original pressure. This is a "constant volume" process:
pressure1 / temperature1 = pressure2 / temperature2
One interesting example of this process at work is to pipe hot steam into a can and then seal it. If the can's walls are thin, once the steam cools off, the pressure in the can will drop, and the external atmospheric pressure will crush the walls of the can.
Now suppose the top of Dexter's rigid container is really an airtight piston that can slide up or down in the container. Dexter again heats up the gas inside the container to twice its original temperature, but this time he lets the piston out so the pressure remains constant as the heat increases. Assuming that he does this quickly so that none of the heat leaks out, the end volume is twice that of the original volume. Similarly, if Dexter cools the gas and pushes in the piston to maintain a constant pressure, assuming no heat leaks in, the end volume is half the original volume. This is a "constant pressure" process:
volume1 / temperature1 = volume2 / temperature2
Now suppose Dexter pulls out the piston to expand the container to twice volume and then lets the gas inside warm up to the outside ambient temperature. The end result will be that the pressure falls by half. Similarly, if he pushes in the piston to compress the container to half volume and lets the gas cool off to the outside ambient temperature, the pressure doubles. This is a "constant temperature" process:
pressure1 * volume1 = pressure2 * volume2
The relationship between pressure and volume, temperature being constant, was observed by the English chemist Robert Boyle (1627:1691), who suggested it in a book published in 1661. The volume and temperature relationship, pressure being constant, was suggested by the French chemist Jacques Charles (1746:1843) in 1787, and the pressure and temperature relationship, volume being constant, was proposed by another French chemist, Joseph Gay-Lussac (1778:1850), who published it early in the 19th century and came up with the combined gas law to cover all three laws.
The relationships in the CGL become more complicated if temperature, volume, and pressure are varied all at the same time -- this is one of the reasons why calculating the effects of compressible flows is so difficult -- but the general effects of changes in pressure, temperature, and volume remain apparent. It should be remembered that gases at typical Earthly conditions are a good approximation of ideal gases, but at extremes of pressure or temperature gases may depart from this nice neat behavior.
* Not incidentally, there is an "ideal gas law (IGL)" that is an extension of the combined gas law, given as:
pressure1 * volume1 = number_of_molecules * R * temperature
-- where "R" is a proportionality constant, the "universal gas constant" -- or "Regnault constant", given in metric units as:
R = 8.3144598 joules per moles * kilograms
-- with the "mole" being a unit of molecules, 6.02E23. The combined gas law is more useful for simple purposes, but the ideal gas law has a very significant point: the pressure and volume is only dependent on the number of molecules, not on the kind of molecules.
The IGL was derived empirically, with the value of R determined from experiments by French chemist Henri Victor Regnault (1810:1878), and named in his honor. The idea that heat was due to molecular motion did obviously imply a link between the ideal gas law and classical Newtonian mechanics. Newton's PRINCIPIA MATHEMATICA pointed out that the pressure-volume relationship discovered by his contemporary Robert Boyle could be explained if a gas was considered as a collection of tiny elastic particles, flying around in free space. However, making a rigorous connection between the two was tricky.
It was possible to model the behavior of a single molecule using Newtonian mechanical principles, envisioning it as a particle with a given velocity that undergoes collisions. The problem was that a gas is made up of a vast number of particles that all have different speeds. Trying to measure or model the individual behavior of each molecule in a gas was obviously impossible.
The solution to this problem was discovered by three 19th-century physicists: James Clerk Maxwell (1831:1879), a Scotsman ("Clerk" is pronounced "Clark" in this case, incidentally); Ludwig Boltzman (1844:1906), an Austrian; and Josiah Willard Gibbs (1839;1903), one of the first major American theoretical physicists. Their approach was to perform a statistical analysis on the large number of particles, using the basic laws of Newtonian mechanics to obtain a "probability distribution" that gave the relative proportions of particles in a given range of velocities for a given temperature. Although tracking all the particles was impossible, it was possible to statistically determine their average behavior.
The analysis, now known as "Maxwell-Boltzman statistics", allowed the IGL to be derived from Newtonian mechanics, linking the "microscopic" world of particle interactions with the "macroscopic" world of the ideal gas law. The details of Maxwell-Boltzman statistics are not very relevant to an introductory thermodynamics text, but the idea is relevant in the broader sense that it introduced the concepts of statistical analysis to fundamental physics: the notion that, although there might be no way to determine the action of the specific particles of a system, the "law of large numbers" would still allow the behavior of that system to be predicted. This powerful technique would be exploited in new directions by 20th-century physics.
* Liquids and solids are generally not very compressible, and so do not follow the same laws as gases. Heat still has an effect on them. Most solids and liquids increase in volume when heated, and decrease in volume when cooled. This is why bridges have "expansion joints" at intervals, to compensate for the changing length of the span due to temperature changes. The change in the size of an object made of a particular material is called its "coefficient of thermal expansion".
One simple practical application of this property is the "bimetallic coil" used in some thermometers. This is a coiled strip of metal with brass on one side and iron on the other. Since the two metals have different coefficients of thermal expansion, as the strip is heated or cooled it will bend one way or another in a predictable fashion, and the raveling or unraveling of the coil could be used to turn a thermometer needle.

The same principle is used in traditional thermostats, though they use an uncoiled bimetallic strip. The thermostat can be set so that if the strip bends to a particular position, it will complete an electric connection, and turn on the heat or air conditioning as need be.
* Heat of course can change a substance from solid to liquid, and from liquid to gas. For example, water is solid ice at low temperatures, but changes to liquid at higher temperatures, and steam at even higher temperatures. Different materials go through such "changes of state" or "phase changes" at specific temperatures. Some materials don't go through a liquid phase, converting directly from solid to vapor, at least under typical Earthly atmospheric pressures, a process that is known as "sublimation". Frozen carbon dioxide sublimates, which is why it is used to cold-pack parcels that have to be shipped, since such "dry ice" doesn't create puddles. Incidentally, water ice sublimates at a low rate: leave an ice-cube tray in a freezer for many months, the ice cubes will gradually fade away, or at least they will if the freezer is opened often and the climate is dry.
The amount of heat that must be added to a substance to produce a phase change is called the "latent heat". Different phase changes have different latent heats: a particular material will have different latent heats of melting, vaporization, or when it applies, sublimation.
At standard atmospheric pressure, water cannot be heated above 100 degrees Celsius, because any additional energy simply vaporizes the water. Boiling water is actually, in a sense, a "cooling" process since it prevents the accumulation of energy. A pressure cooker is used to obtain higher water temperatures. When water condenses again, the latent heat that vaporized the water is released.
The proportion of water vapor in the air is referred to as "humidity". There is a maximum level of humidity that air can support, which increases with temperature since water condenses back to liquid more easily at low temperatures than high. When the air can accommodate no more water vapor, it is said to be "saturated". Humidity is usually given in terms of "relative humidity", or the ratio of actual water vapor to the saturation level. At 50% relative humidity, the air contains half the amount of water vapor that it is capable of supporting, and at 100% relative humidity the air is saturated.
The evaporation of water is used for cooling in the "evaporative cooler" or "swamp cooler", a simple household cooling device used in dry, warm climates. It consists of little more than a fan pulling air through a filter through which water is pumped. The air causes the water to evaporate, moistening and cooling the air. It is substantially cheaper to buy and operate than a conventional air conditioner, whose operating principles are discussed in the next chapter.
An evaporative cooler is ineffective in hot humid climates since the rate of evaporation slows, and in fact it may simply make a living space more humid and sticky. A more effective approach for such climates is to build an array of terra-cotta tubes, with the array set on its side. Water trickles down over the tubes as a fan blows air through the array -- avoiding the humidity problem.
Incidentally, water is an unusual substance in that it actually expands when frozen, due to the way its molecules rearrange themselves. This is a fortunate circumstance for life on Earth, since if it were not so, all ice forming on the ocean would sink to the bottom and gradually build up a reservoir of ice that would make the planet a permanent "icebox".
* Gases, liquids, and solids that are being heated, but not changing state, have a "specific heat" that defines how much energy must be added per unit mass to raise the temperature of unit mass of the substance one degree. The specific heat of water, for example, is by definition one calorie per gram per degree Celsius. Incidentally, the specific heat of water is unusually high, and so it takes more energy to heat water than most other substances. In the case of materials that are compressible, specific heat has to be rated in terms of whether the materials are held at constant pressure or at constant volume.
The concept of specific heat leads to the notions of "thermal mass" and "heat reservoir". For example, a lake has thermal mass, in that it will require energy and involve a certain delay to heat it up, and once heated up will act a reservoir of heat, slowly releasing it back to the environment.
BACK_TO_TOP* Heat is transferred by three processes:
Solid and opaque objects support heat transfer primarily through conduction. Different materials have specific "thermal conductivities", or rates of heat flow through them. For example, metals generally have high thermal conductivities: if Dexter wears metal-rimmed sunglasses on a cold day, they will painfully drain the heat right out of his nose. Plastics generally have lower thermal conductivities, and it is much more comfortable to wear plastic-rimmed sunglasses on a cold day.
Materials with low thermal conductivities are, naturally, used as thermal insulators for homes and buildings. Gases generally have low thermal conductivities, and most forms of home insulation are basically designed as "gas traps". The most vivid example of this principle is sheet plastic foam insulation, which is filled with bubbles of gas. Incidentally, the insulating capability of commercial insulation is specified by an "R-value", which is inversely related to the thermal conductivity. The higher the R-value, the better the insulator. For example, thick fiberglass insulation has an R-value of almost 20, while double-paned glass has an R-value of a little over 1.
For a high degree of thermal insulation, a "dewar flask" is used. The common consumer "Thermos bottle" is a cheap type of dewar flask. A lab-quality dewar flask consists of a double-walled vessel made of Pyrex glass with silvered surfaces and the space between the two walls evacuated. A vacuum has no thermal conductivity; of course it can't support convection; and the silvered surfaces reflect radiation and so limit loss by that route. The neck and cap of the flask end up providing most of the thermal conduction, and so are generally made as small as possible.
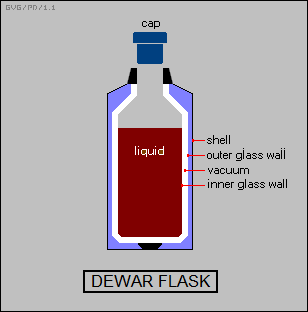
Extreme cooling requires a "double dewar" scheme, with one Dewar flask contained in a second, and the space between the two filled with a cryogenic fluid such as liquid nitrogen (with a boiling point of 77 degrees Kelvin) or, for really chilly applications, liquid helium (with a boiling point of 4 degrees Kelvin).
Infrared telescopes launched into orbit around the Earth require extreme sensitivity to observe distant and cool cosmic objects. One of the problems with infrared telescopes and other infrared imagers is that they can't pick up a target that's cooler than they are, since their own thermal emission will drown out the infrared emitted by the target. As a result, space infrared telescopes are often built as (very large) double-dewar flasks known as "cryostats", with an infrared telescope built inside the inner dewar flask. They may also have a reflector shield made of multiple layers of plastic, separated by spaces exposed to the vacuum, to reduce solar heating and conserve their cooling helium. As mentioned in an earlier chapter, they are often put into halo orbits at the Earth-Sun L2 point so they can always keep the shield pointed at the Sun.
* The physical configuration of an object affects its ability to retain heat. The simple general rule is that an object retains heat better if the ratio of its surface area to its volume is kept as low as possible. This is why people adapted to cold climates tend to be short and stout, while those adapted to hot climates tend to be tall and slim, giving them a greater ratio of surface area to volume to help them get rid of heat through convection and radiation.
Air-cooled engines will have sets of fins around the cylinders to allow the heat to be dissipated. Similarly, inspection of the circuit board for, say, a personal computer, will reveal that the processor chip is usually fitted with a finned plate or "heatsink" to dissipate its heat of operation. A personal computer will also generally have an electric fan to get rid of the warmed air inside of the enclosure and draw in cooled air. As processors become more powerful they generate increasing amounts of heat, and some do have liquid cooling to deal with it.
* The behavior of heat in a physical system is described by three rules, known as the "Laws of Thermodynamics". The Laws of Thermodynamics govern the efficiency of engines, and also rule out "perpetual motion machines".
Thermodynamics is an abstract field even by the standards of physics. To understand it, a few formal definitions must be set down first. The most important is that of a "thermodynamic system", which is defined as a domain bounded in space where heat can flow across the boundaries in either direction.
The properties of a thermodynamic system at any one time define its "state". The most important properties are the "thermodynamic variables" of temperature, pressure, and volume, but there are other variables, such as density, specific heat, and the coefficient of thermal expansion. If the properties of a thermodynamic system do not change over time, and if there are no changes in its configuration and no net transfers of heat across the boundary of the system, the system is said to be in "thermal equilibrium". If the thermodynamic system moves from one state of thermal equilibrium to another, a "thermodynamic process" is said to have taken place.
A thermodynamic process can be "reversible" or "irreversible". A reversible process can be run in one direction, and then be reversed to return to the same state that it started from with no net change in system energy. An irreversible process can be run in one direction, but will require a net input of system energy to reverse it.
* There are four Laws of Thermodynamics. Originally, there were only three, but later physicists decided that a fourth law was required; since this law was basic to the other three, it was called the "Zeroth Law of Thermodynamics" instead of the "Fourth Law of Thermodynamics". The Zeroth Law is basically a definition of the term "temperature". It states that if two thermodynamic systems are in thermal equilibrium with a third thermodynamic system, then the first two systems are in thermal equilibrium with each other. They will all share the same "temperature".
* That formality out of the way, the "First Law of Thermodynamics" defines heat. The First Law of Thermodynamics stems from the work of Joule, Mayer, and Helmholtz, and amounts simply an extension of the law of conservation of energy to include heat. It states that when a warm object (thermodynamic system) is brought into "thermal contact" with a cooler object, meaning a connection that allows the transfer of heat, a thermodynamic process will take place that eventually brings them to the same temperature. The process transfers "heat energy" between the two objects. In metric units, heat energy is measured in joules.
The amount of heat transferred into a system, plus the amount of work done on the system, must result in a corresponding increase in the thermal energy of the system. The First Law further implies that if any work is done by the system, it must drain the internal energy of the system. A system where work can be done without draining the internal energy of the system is referred to as a "perpetual motion machine of the first kind". The First Law rules out such machines.
* The "Second Law Of Thermodynamics", established through the work of the English physicist William Thompson, later Lord Kelvin (1824:1907) -- the "Kelvin" temperature scale is named after him -- and the German physicist Rudolf Julius Emanuel Clausius (1822:1888). It is by far the most important of the four laws, and some have suggested that it really should have been the First law, not the Second, though in practice the Zeroth and First laws act as necessary steps up to it.
The Second Law requires definition of a property known as "entropy" that was devised by Clausius. In formal thermodynamic terms, classical physics defines entropy as:
heat_transfer
entropy = --------------------
absolute_temperature
-- meaning that in metric terms, it's given in joules per degrees Kelvin. The Second Law states that the entropy of an "isolated" or "closed" system, meaning one where there is no transfer of energy across its boundaries, can never decrease; an "open" system, in contrast, features a transfer of energy that can create an increase in entropy.
In more informal terms, entropy is a measure of dispersal or "smearing out" of energy. If we have a tank full of a hot gas and a tank full of a cold gas, energy is concentrated in the tank full of hot gas, and as discussed in detail later this difference in energy concentration can be used to do work. Mix the two tanks together until they're at the same temperature, then the concentration of energy has been lost even though -- given perfect insulation -- no energy is lost. The significance of the specific form of this definition will be discussed in the next chapter. Entropy can actually be expressed in other ways, and the definition of the term has to be carefully considered for any given scenario.
The concentration of energy in the tank of hot gas is expressed in a concept known as "free energy", the energy available to do work in a system, roughly the opposite of entropy. The free energy is used up doing work in a system, with entropy rising as the free energy is expended. In a closed system, eventually the free energy runs out and no more work can be done; in an open system, the free energy is replenished from the outside Universe, and things will go on running as long as the replenishment continues.
A closed system where the entropy decreases is referred to as a "perpetual motion machine of the second kind". The Second Law rules out such machines even though they do not violate energy conservation -- more on this later.
* The "Third Law of Thermodynamics" is a bit of an anticlimax after the other laws. It simply recognizes the existence of the absolute temperature scale, and states that absolute zero can never be attained in practice in any finite number of cooling steps. A cooling system can in principle approach absolute zero by a narrower and narrower margin, but it will never actually reach absolute zero.
* In modern times, as mentioned earlier, the concept of caloric has been replaced by an understanding of heat as the motion of the molecules of a system, using statistical methods based on classical mechanics to determine the average behavior of a large number of molecules. In this view, temperature is a measure of the average kinetic energy, or essentially the motion, of the molecules of a system. A temperature increase means that the average kinetic energy has increased.
Similarly, heat transfer between two thermodynamic systems is caused by collisions between individual molecules of the systems. The collisions continue until on the average the net energy passing across the boundary between the two systems is zero, meaning the two systems have achieved thermodynamic equilibrium.
The First Law of Thermodynamics, then, exactly corresponds to the classical law of conservation of energy. The molecular nature of the Second Law of Thermodynamics is a little more subtle, and basically expresses entropy as the measure of the "probability" of a system. Given a large number of molecules in a thermodynamic system, probability dictates that the molecules will be moving in many different directions (high entropy) than in one direction (low entropy).
* The Second Law sets a direction of time, or "arrow of time", in the direction of increasing entropy. On the microscopic atomic scale, interactions are generally reversible: if we make a video of a collision between two atoms, it will be just as valid if the video is run forward or in reverse. At a macroscopic level, this can be also seen in, say, collisions of billiard balls: if a video is made of two balls colliding, ignoring friction it will be valid if run forward or in reverse. However, if we make a video of the "break" at the beginning of a pool game, in which the orderly balls are scattered over the table, it will be very obvious whether the video is run in forward or reverse. In broad terms, entropy ensures that time only runs in the forward direction.
Modern physics would show that this arrow of time had a catch, and also show the solution. Given a system with a low entropy, or low probability, in the present, then it is of course likely to evolve to a state with high entropy, or high probability, in the future. This is what the Second Law basically says. The catch is that, given a system with low entropy / low probability in the present, then the odds would suggest that the system also had high entropy / high probability in the past. Of course, this isn't the way things really work, as a rule, in the past the system had even lower entropy and probability.
It was the discovery of the Big Bang, the primordial explosion that created the Universe we live in, that provided the explanation. The Universe began in a state of high energy and uniformity with low entropy, or in other words the Big Bang provided a "zero reference" for entropy, and the entropy has been increasing ever since. Put simply, the Universe is running thermodynamically downhill from an initial height, and that defines the arrow of time on the macroscale. Some have speculated that if the Universe were to cease to expand and fall back in on itself, then time would reverse, though this idea is argued.
This is getting well off track, the argument being only of interest to physicists. For all practical purposes, it can be and is taken as a given that time only flows in the forward direction, that entropy always increases overall. From the microscopic physics point of view, there is no reason that the motion of all the molecules in a brick that has been dropped to the ground could not point straight up, causing the brick to fly back spontaneously into the air. However, this configuration is vanishingly improbable. It simply doesn't happen -- it is an irreversible process.
Similarly, there is no reason on the microscopic scale that air molecules could not transfer net heat into a brick, making it warmer, but this is improbable as well. A hot brick will release its heat into cooler air, but cooler air will not warm up a brick. Heat always transfers from a warm object to a cooler one, never the reverse; it always flows "downhill" instead of "uphill". In fact, this is actually just another way to state the Second Law.
* It should be noted that the classical Clausius definition of entropy is not entirely accurate, there being cases where it falls down. Modern physics uses a much more refined definition of entropy, devised by Boltzman and based on statistical concepts:
entropy = constant * natural_log( number_of_available_states )
In essence, Boltzman's read on entropy says that when we have "high quality" energy, with a high temperature difference, the number of available states, the entropy, is smaller than it is when it's been "smeared out" to "low quality" energy, with a low temperature difference. However, as far as simple physics goes, the Clausius definition does the job and the subtler Boltzman definition is overkill; it is not used for engineering calculations. It is simply given here as a connection to more detailed studies. In the "macroscale", Boltzman's definition of energy gives much the same results as Clausius's definition.
It should be noted that a branch of theoretical math known as information theory also has a concept of "entropy", in the form of an equation that gives the amount of information that can be sent over a communications channel, such as a telephone line. The equation turned out to have exactly the same form as that of Boltzman entropy and so the amount of information defined by the equation was defined as "entropy".
This has led to a long-running argument over whether there is really any connection between information theory and thermodynamics. Some physicists insist there is; some on the other side of the argument suggest that use of the term "information" needs to be completely banned from discussions of thermodynamics. It appears the pro-information faction is winning out -- but it hardly matters, since the argument is of no great interest to anyone but physicists.
* Incidentally, textbook thermodynamic analysis also uses a concept known as "enthalpy" -- which sounds obscure, but it's simply defined:
enthalpy = heat_energy + work_done
Not surprisingly, using metric units, enthalpy is measured in joules. It's no more than a convenient calculational shortcut, and not of great interest in an introductory thermodynamics document. Anyone moving on to a more thorough study of thermodynamics will find it useful, of course.
BACK_TO_TOP* There is no more commonly misunderstood concept in physics than the Second Law of Thermodynamics, or SLOT for short. The trouble really boils down to the fact that there has been an inclination to equate "entropy" with "disorder", implying that the Second Law claims the Universe has a natural tendency to "disorder", in exactly the same way a room becomes messy over time. It would seem, then, the Universe is simply falling apart forever.
So, does "entropy" actually mean "disorder"? Yes and no, mostly no. The Second Law tells us that if we mix a hot gas, consisting of energetic molecules, and a cool gas, consisting of unenergetic molecules, there's no way the energetic and non-energetic molecules will ever spontaneously sort themselves out. This degrading of molecular energy states is what is meant by entropy; the energetic molecules have lost their free energy in being mixed, and we can't get work out of them any more.
Entropy does mean disorder of a certain specific sort, a smearing out or dispersal of energy. The problem with calling entropy "disorder" is that people have much broader ideas of "disorderliness" -- messy rooms, for example -- but entropy has nothing in particular to do with general disorderliness and untidiness, and it is very misleading to imply that it does. Defining the term "entropy" simply as "disorder" is, if not completely wrong, at least asking for trouble, and in modern times it is discouraged.
Although by all evidence the Second Law absolutely cannot be violated in its own domain of concern, it's entirely obvious that order of various sorts arises spontaneously from disorder in other domains all the time. It is true that the formation or dissociation of molecules can result in changes in entropy, but only to the extent that formation or breaking of chemical bonds affects the energetics of the system. Elaborate and orderly crystals -- grains of salt, snowflakes -- are easily formed; the thermodynamics of crystal formation are well understood, and there's an increase in entropy in the process. For another example, if a colored dye is mixed with water, it will be impossible to sort out the mix -- unless the dye is in the form of a light oil, in which case it will promptly segregate from the water to form a thin layer on the surface.
As such illustrations suggest, the Second Law only deals with the narrowly-defined concepts of "order" and "disorder" applying to thermodynamics, and it is not concerned with, say, the spatial arrangement of atoms or other particles. Consider a bin with a partition separating a mass of blue balls and a mass of red balls; pull out the partition and shake the bin, the two colors of balls will mix up and will never spontaneously sort themselves out again.
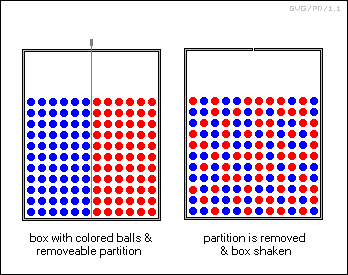
However, if the red balls are twice the size of the blue balls, shaking will cause the red balls to rise to the top of the mix and the blue balls to the bottom. Separation techniques operating at about that level of sophistication are common industrial processes, for example in the refining of ores. That is of course a controlled process, but unwanted spontaneous separation of mixtures can be a real problem in materials handling. Geologists can also point out that normal geological processes often create concentrated localized deposits of minerals. Are these processes violations of the Second Law? No. The Second Law is not directly concerned with the spatial ordering involved in the formation of a crystal structure or of mineral deposits.
In fact, to the extent the Second Law affects such forms of order, it may well promote them: as energy rolls down the "hill" towards increasing thermal disorder, it has a tendency to produce complex phenomena, including some that seem counterintuitive. For example, would anyone think that water will spontaneously flow back upstream, against the law of gravity? It is actually easily seen that it can, if fleetingly, from vortexes in streams. We see other examples along this line arising at higher scales, in the form of cyclonic storms and spiral galaxies.
Along the same lines, it must be pointed out that matter features a scale of energetic interactions, from the very strong energies that hold atoms together, to the moderate energies that hold molecules together, down to the mild energies that cause interactions between molecules. The interesting thing is that this hierarchy of energies directly corresponds to the number of possibilities of interactions. The result of the strong energies that hold atoms together is that there's less than a hundred possible stable atoms; the moderate energies that hold molecules together correspond to vast numbers of molecular arrangements; and the mild energies involved in interactions between molecules permit unbounded opportunities for complex arrangements of matter. Such arrangements obviously can include processes that operate in sequences or cycles, with the cycles potentially leading to open-ended increases in complexity. In other words, the direction of decreasing energies associated with an increase in entropy are linked to a vast increase of the number of possibilities for interactions.
In other words, the direction of decreasing energies associated with an increase in entropy are linked to a vast increase of the number of possibilities for interactions. On the basis of a simple-minded interpretation of the SLOT, we couldn't imagine a Universe that ever amounted to much more than it did at the beginning, a dispersed thin fog of hydrogen with traces of helium evenly distributed throughout space. In reality, heavier elements were synthesized by natural processes from lighter ones; stars and planets were formed from the elements, making up intricate stellar and planetary systems; elaborate molecules and crystals arose on the planets, with the planets also developing surface features like mountains and oceans, as well as complex weather patterns.
If the emergence of order actually violated the SLOT, then that would also make cars, airplanes, and personal computers impossible -- after all, it's not like human beings can violate the SLOT. Yes, that's an absurd argument, but it's really no more absurd than the claim that the SLOT rules out the spontaneous emergence of order. The SLOT says that the Universe is running down, running out of free energy; what it does not say that, left to itself, it is falling apart like a decrepit old house.
BACK_TO_TOP* As noted previously in this document, the law of conservation of energy rules out most perpetual motion machines, the "perpetual motion machines of the first kind", while the SLOT rules out "perpetual motion machines of the second kind" that don't violate energy conservation.
A typical example of such a machine may incorporate a screen that, so the inventor claims, will allow fast-moving molecules to pass through and block slow-moving molecules, resulting in the buildup of a temperature difference between the two sides of the screen that could then do useful work. The screen might have tapered passages, with large holes on one side of the screen narrowing to small holes on the other, which supposedly will tend to pass more fast-moving molecules than slow-moving ones.
Such schemes still end up being busted by the physics police: the "magic screen" described above is a fantasy. In practice, even if there were originally a temperature difference across the screen, it would quickly balance out. As SCIENTIFIC AMERICAN magazine put it, in a column on rejection letters written as Japanese haiku poems:
Though the specs look nice, A stop sign halts your machine. Thermo's second law.
However, there are also a number of physicists who like to play the perpetual-motion game as a thought experiment to see what interesting insights it may provide. Nobody sensibly thinks for an instant that there is any way to get around the law of conservation of energy, but could some machine be invented that exploits a loophole in the second law of thermodynamics?
The most famous of these theoretical perpetual motion machines is "Maxwell's Demon", originally devised by James Clerk Maxwell, which amounts to a "smarter" approach to a magic screen. In this scheme, the system consists of two chambers containing gas molecules. The chambers are separated by a door that is opened or shut by a tiny "demon". When the demon spots a fast-moving molecule in the first chamber, it opens the door to let it into the second, and keeps the door closed for slow-moving particles. In this way, the demon can build up a stockpile of energetic molecules that can be released or otherwise used to do useful work.

While obviously there is no demon available to do the job, it was still hard to understand why such a scheme could not be used in principle to build perpetual-motion machines, and through the invention of the demon Maxwell was posing the question to later generations as to why it wouldn't work. Incidentally, Maxwell did not name the demon after himself; it was named by others later in honor of Maxwell.
In 1929 by the Hungarian physicist Leo Szilard (1898:1964) proposed a solution. Szilard asked: how does the demon know which molecule is moving faster than the others? Basically, he'd have to "turn on the lights" in the chamber so he could see the molecules, and even if he only used a selective beam of light to do so, Szilard showed that the energy expended in sensing the motion of the particles would always be greater than the amount of energy gained by sorting the molecules out. The Second Law wasn't violated.
However, Szilard came up with a simple variation on Maxwell's Demon, sometimes called "Szilard's Demon", that evaded this obstacle, taking things more or less back to square one. Eventually studies showed that there was a certain unavoidable amount of energy expenditure in making a decision, and this amount of energy was still enough to guarantee the Second Law.
* There have been a number of variations on the theme of Maxwell's Demon. An interesting one was devised by Dick Feynman, who enjoyed being clever and unorthodox. His demonic "motor" was envisioned as a microscope gear connected along its axis to a small paddle wheel. The gear was ratcheted so that it can only move in one direction. If the Feynman motor was placed in a gas or fluid, molecules would strike the paddle wheel. Since the gear could only move in one direction, the paddle wheel could only turn one way, and useful work could be obtained from random (Brownian) molecular motion. Feynman figured that his motor could lift fleas.
Having presented this idea, Feynman then demolished it. The weak point was the spring-loaded ratchet. Thermal action would also cause the ratchet to bounce out of place, and the skewed configuration of the gear teeth would make it more likely the gear would move in reverse if that happened. The jerk back through the paddle wheel as the ratchet snapped back into place would dump heat back into the medium.
Feynman's motor was a theoretical toy, but others have taken it a bit more seriously: nanotech researchers have indeed developed atomic-scale paddle wheels with a ratchet. By themselves they are useless, but work has been performed to allow them to be driven by chemical reactions or other inputs.
BACK_TO_TOP