
* As final notes in this document, this chapter discusses interest footnotes to classical cryptology -- including the clever Hagelin M-209 cipher machine, cryptological frauds or "pseudocryptology", and classic mechanical locks.
* One of the interesting footnotes to telecipher machines was a remarkable hand-operated, completely mechanical, man-portable cipher machine used by the US military in World War II, with the manufacturer's designation of "C-48" and military designation of "M-209". The M-209 was designed by Swedish cryptographer Boris Hagelin in response to a request for such a portable cipher machine, and was an improvement of an earlier machine, the "C-36".
The M-209 was about the size of a cigar box, and represented a brilliant achievement for pre-electronic technology. It is included in this chapter because it used a wheel scheme clearly related to that of a telecipher machine.
* From the code clerk's point of view, the M-209 was simple to operate. There were six wheels on top of the box that each displayed a letter of the alphabet through a window, and he could set these six wheels to provide the key for enciphering a message. This only gave a limited number of possible keys, but as is discussed below, there were also internal settings that could provide a much greater range of key settings.
To actually encipher a message, the code clerk first set an "encipher-decipher" switch to the "encipher" position, rotated an "indicator" knob labeled with the letters of the alphabet on the left of the box to the first letter to encipher, and then pushed down on a lever on the right side of the box. This printed an enciphered letter on a paper strip that reeled out the top of the box. The code clerk then enciphered all the other letters in the message in the same way, resulting in a listing of the ciphertext on the paper strip, which could then be read off for transmission by Morse code.
By the way, the lever on the right was called the "power handle", though the only power provided to the M-209 was muscle power. There was a "letter counter" indicator on top of the box, something like an automobile's odometer, to let the code clerk know how many letters he had enciphered in a message, so he didn't lose place.
Deciphering the message was just as simple. The code clerk on the receiving end set the six wheels to the same initial positions, turned the encipher-decipher switch to "decipher", entered the first letter of the ciphertext on the knob on the left, and pressed the power handle to print out the first letter of the deciphered text on the paper strip. He then went through all the ciphertext letters to print out the deciphered message on the paper strip. It typically took about two to four seconds to encipher or decipher each letter, so the scheme was reasonably fast.
* The M-209 was unsurprisingly more complicated under the hood. In broad outline, when enciphering a message, pressing the power handle activated a clever mechanical enciphering mechanism that advanced a printwheel a certain number of letters ahead of the plaintext letter entered on the indicator knob, and then printed the appropriate ciphertext letter on the paper strip.

The printwheel was linked to the indicator knob, so that its position was always set to the plaintext letter before pressing the power handle and moving the printwheel through the offset. Of course, the offset changed with each plaintext letter entered, otherwise this scheme would have simply implemented a totally insecure Caesar shift cipher.
The mechanical enciphering mechanism included two assemblies. One was an assembly of six wheels. Each wheel had pins that could be pushed through the wheel in either direction. A pin was pushed to the right to make it operational and pushed to the left to disable it. All six wheels were advanced one position with each push of the power handle, but the wheels had different numbers of pins, with 26, 25, 23, 21, 19, and 17 positions, meaning that the arrangement of wheels would only repeat itself after a period of 101,405,850 letters.
This assembly was very much like that found in a telecipher machine. The other assembly, the "cage", was much more unusual. It essentially translated the positions of the wheel assembly to the cipher offset of the printwheel. The cage looked exactly like its namesake, resembling a cylindrical birdcage with 27 bars held between two disks. The cage was laid on its side in parallel and behind the wheel assembly, and with the printwheel mechanism to the left.
The bars of the cage could slide and protrude out of the cage assembly on the left. When the power handle was pressed, the cage was spun around through a complete rotation, and the bars were selectively pushed out the left side as governed by the pin settings of the wheel assembly, forming a "variable toothed gear". The number of bars pushed out gave the printwheel offset, with an intermediate gear advancing one position for each protruding bar to move the printwheel forward. At the end of the power handle stroke, the letter was printed, and all the bars pulled back into the cage in preparation for enciphering the next character.
There were two moveable "lugs" on each of the 27 bars, and the lugs could be set to engage any of the six wheels. For example, one lug on a bar might be set to engage wheel 2, while the other might be set to engage wheel 5. There were also two "neutral" positions on each bar, allowing one or both of the lugs to be set so they never interacted with a wheel at all.
The wheels interacted with the cage through a set of six "guide arms", one for each wheel. When the code clerk pushed the power handle, each wheel with the current pin set to the right would activate its corresponding guide arm, while the guide arms of wheels with the current pin set to the left and disabled would remain inactive. The cage would then spin around through all 27 bars. Those that had lugs in the same position as a wheel with an active guide arm would be deflected to the left to form the variable toothed gear, while those bars where either lug didn't hit a guide arm would stay in place.
The mechanism worked much the same way for deciphering a message, except that the direction of the printwheel's offset was reversed, moving it back to translate from the ciphertext letter to the plaintext letter.
A complete key for the M-209 amounted to not only setting the wheel positions, but also the pins on the wheels and the positions of the lugs on the bars. Performing such a full configuration was unsurprisingly very time-consuming, and so it was usually only done at intervals, not with every message sent.
* The M-209 was good for its time, but it was by no means perfect. As with Lorenz, if a codebreaker got hold of two overlapping sequences, he would have a fingerhold into the M-209, and its operation had some distinctive quirks that could be exploited. It was, however, perfectly adequate for tactical use and remained in service in the Korean War. Hagelin built about 140,000 M-209 / C-48s, and got very rich off of the thing.
A German cryptologist named Fritz Menzer actually built cipher machines based on Hagelin technology, though no doubt Hagelin never got any royalties off them. Menzer's "Schluesselgeraet 1941 / Cipher Device 1941 / SG-41" was a purely mechanical device, with an internal organization along the lines of the M-209 but larger, with a real keyboard. It was actually put into limited production, with about a thousand built for use by the Abwehr, the German intelligence service, which operated them from 1944.
The SG-41 was supposed to have been a standard tactical cipher machine, but the Germans had only limited supplies of lightweight metals such as magnesium and aluminum, and it was simply too heavy for tactical use. Menzer also worked on two other cipher machines based on Hagelin technology, including a follow-on to the Enigma, the "SG-39", and a simple but fairly strong handheld cipher machine, the "Schluesselkasten (Cipher Box)". Neither of these machines reached production. Had the Menzer devices been put into service, they would have certainly thrown a curve at Allied cryptanalysts, though they were certainly no more uncrackable than the M-209.
After the war, Hagelin came up with an improved model of the M-209, designated the "C-52". The C-52 featured a period of 2,756,205,443; wheels that could be removed and reinserted in a different order; and a printwheel with a mixed alphabet. However, the C-52 was one of the last generation of the classic cipher machines, since by that time new digital technology was permitting the development of far more powerful ciphers.
* Incidentally, although Hagelin died in 1983, his firm Cypto AG survived him, being an influential player in the global cryptosystems market up to its liquidation in 2018. In 2015, redacted US government documents came to light that revealed that in 1955, Hagelin came to an unwritten agreement with William Friedman to provide technical details of Hagelin cryptographic machines to US and British intelligence, along with a list of which countries had bought those machines. That list never included the Soviet Union or China; they wouldn't have trusted crypto gear from a Western source in any case.
Eventually, suspicions arose that Crypto AG products were compromised. In 1986, a discotheque in West Berlin that was frequented by American servicemen was bombed; US President Ronald Reagan said that intercepted communications pointed to Libyan involvement in the bombing, leading to a US air strike on Tripoli. The story of the communications intercept was not universally believed, with suspicion falling on Crypto AG.
Crypto AG officials denied all such accusations -- but in 2020, investigation showed conclusively that from 1970, the US Central Intelligence Agency (CIA) and German BND intelligence were the secret owners of Crypto AG. It was a reverberating scandal in Swiss society, all the more so because the Swiss government was obviously aware of the arrangement, and tolerated it.
BACK_TO_TOP* The Friedmans, as noted, spent considerable effort on the search for hidden ciphers in the works of Shakespeare. They were not alone in such efforts; the topic of hunting for hidden ciphers in great works of literature, particularly the Bible, is a subfield of cryptology in itself, known as "pseudocryptology". Some sources call it "enigmatology" but that term is more generally applied to the study of puzzles.
The field goes back to at least 1884, when an American named Ignatius Donnelly published THE GREAT CRYPTOGRAM, making a case that Francis Bacon actually wrote the plays of Shakespeare. Donnelly was an interesting sort. He served three terms in the US Congress; after being voted out, he turned to writing popular works of pseudoscience that promoted such ideas as the historical existence of Atlantis and linking Biblical disasters to a cometary impact. His ideas resurface in different forms in fringe literature on a periodic basis.
The usual approach of pseudocryptologists is to scan through the text of interest and take out letters at intervals, for example every 13th letter, every 100th letter, or every 1,617th letter. They then arrange the letters in a block and see if patterns pop out. The patterns are typically identified as scrambled words buried in a stream of gibberish. It is not too surprising that one can actually extract seemingly sensible remarks using this scheme. It's about on a logical level with, say, playing the music of the Beatles backwards and listening for secret messages left by John Lennon. (Actually that might not be such a good comparison, since Lennon was potentially crazy enough to do such a thing.)
A modern advocate of such hidden codes, Michael Drosnin, published a series of BIBLE CODE books that listed predictions of a wide number of events hidden in the Bible. The books made the best-seller lists, despite the fact that most of the predictions identified by Drosnin in his books were "postdictions", of events that had already happened. His predictions of actual future events, such as the end of the world in the year 2000, were somewhat inaccurate.
Drosnin challenged critics to find similar predictions about, say, the assassination of a prime minister in MOBY DICK, and so an Australian mathematician named Brendan McKay went out and did precisely that, identifying "predictions" of nine such assassinations. Similar exercises were performed on WAR AND PEACE and other classics. However, this was only the latest iteration of a game that's been going on for a long time, since the Friedmans performed similar refutations against the Baconians.
Pseudocryptology also shows up in pop fiction, where it is harder to object to, since nobody claims it should be taken seriously. A popular modern example was Dan Brown's 2003 novel THE DA VINCI CODE and the Tom Hanks movie made from it, which involved a search for secret documents written by the Italian Renaissance scholar Leonardo da Vinci that disastrously compromised Christianity.
The book invented a cryptological device called a "cryptex", supposedly invented by Leonardo but really dreamt up by Brown. It looked a bit like a Bazeries cylinder, consisting of a cylinder with labeled rings and a few frills, but the order of the rings was fixed and the device was simply a locked container with a document inside. Dialing in the proper password opened the cryptex; dialing in the wrong password broke open a vial of acid inside the device, destroying the document inside. The cryptex was amusing, but not really much more impressive than a bicycle lock. Readers pointed out that it would have been easy to disable the self-destruct system: just chill the device so the acid was frozen solid, allowing combinations to be tried out at will.
The Navajo code-talkers have been something of a fad in pop fiction as well, and one TV show even had agents trying to decode old documents written in Navajo code talk. Although there are some websites that have text of Navajo code talk, it's just as an educational device; Navajo code talk was never intended to be used as a written code, and it would have been fairly easy to crack if it had, since it would have then been little different from any other code. TV and movies also occasionally have scenes where the heroes crack government or military encryption with a laptop PC, providing a little amusement for viewers who have some familiarity with modern cryptosystems. One such tale had a sorceress pulling that trick, but she admitted she had to use magic to help. "Oh, but don't they always?"
* There are other interesting topics along the cryptological fringe. In 1912, an American rare-book dealer named Wilfrid Voynich was prowling through the library of a Jesuit college near Rome, Italy, when he chanced upon a strange centuries-old document. It was a book with large numbers of drawings of fantastical plants and animals, not to mention naked women bathing. This would have been something of an odd find in itself, but what made it really interesting was that it was written in an entirely unfamiliar language.
There was a 17th-century letter tucked into the document that explained it had been purchased by the Holy Roman Emperor Rudolph II in 1586, for the substantial sum of 600 gold ducats. Several scholars tried to decipher the mysterious script during the next century, and then -- sort of like the Ark of the Covenant in the movie INDIANA JONES & THE LOST ARK -- it disappeared into the archives for centuries. Voynich publicized the text and cryptologists tried to crack it, but nobody has ever had any success. Even cryptographers from the US Navy OP-20-G, at something of loose ends at the end of World War II, gave it a shot and got nowhere.
Several people did claim they decrypted it, but the decryptions tended to be nonsensical, and to the extent that they weren't, the would-be codebreakers claimed that different codes were used in different places in the manuscript. Their claims were not taken seriously: obviously, they were simply cooking their methods arbitrarily to get results they liked.
There is a strong suspicion that the "Voynich manuscript", as it is now called, was nothing but a scam, possibly concocted by the English conman Edward Kelly, and the text is just gibberish. However, analyses show that the text has a high degree of structure, not at all consistent with simple random text. On the other hand, it is too regular to be consistent with real languages.
Although it may be impossible to prove that the Voynich manuscript is gibberish, modern research has shown that it is indeed possible to generate random "Voynichese" text that has much the same appearance as that in the document. All it requires is a small set of ordered tables of syllables and a somewhat larger set of grilles with three holes in it them ("Cardan grilles"). Different pages can be assembled by using a different table with a different grille.
Kelley, who was known to be hanging around the court of Rudolph II at the time of the sale of the document, was also known to be familiar with Cardan grilles. It probably wouldn't have been too difficult to write real text in a code, but it would have been easier and faster to simply write gibberish, and it would have also been a safer scam: if nobody could make sense of the text, nobody could extract any clues that would reveal the fraud.
BACK_TO_TOP* As another footnote to classical cryptology, there is the parallel history of mechanical locks. For much of their history, humans lived in hunter-gatherer tribes, which were often nomadic, people not staying in any one place indefinitely. With the rise of farming, very roughly in about 10,000 BCE, they started to become more settled, living in villages from generation to generation. The rise of farming meant everyone could stay fed without having to grow or gather or hunt food on their own. Villages led to cities and nations from very roughly about 3,000 BCE.
When humans lived in tribes, they had little concept of privacy. Everybody in a tribe knew everyone else, and there was no keeping secrets. Once humans settled in cities, however, this familiarity broke down, with people having a need for privacy and security, to protect themselves and their belongings from strangers who might assault or rob them.
The most basic security technology is, of course, the wall; people could build houses or other structures to keep strangers out. Walls inevitably meant doors, and means of securing doors against unwelcome visitors. Doors could be bolted from the inside for protection, but not when nobody was home to pull the bolt and let others in. That led to the invention of locks and keys.
The oldest known lock was found in Iraq, being dated to about 4000 BCE. The device was a "pin lock", in which a key raised a set of pins to a given height, releasing a bolt. The ancient Egyptians improved slightly on the design and made much more use of it. They also made some of their locks partly out of brass instead of wood, but of course the brass locks were much more expensive.
The simple key-&-pin lock spread from Egypt to Greece and thence to Rome. The Romans were able to build smaller locks that could be used on chests and drawers. Apparently, wealthy Romans like to wear keys as decorations, to show they were rich, with possessions that needed protection. They were very crude locks, easily picked, a defense only against casual intrusion. The Romans also had padlocks and simple combination locks.
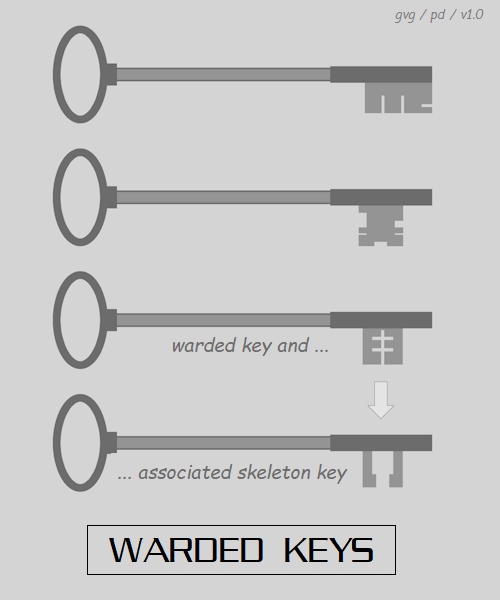
* In the Middle Ages, locks moved up from the feeble key-&-pin lock through the introduction of the "warded lock". It wasn't a completely new idea, the basic concept going back to Roman times, but it wasn't fully developed until medieval times.
The key for a warded lock explains it all: it's something one might see in historical movies, with a long shaft and a patterned metal tab at the end. The key was inserted into the keyhole, to enter a cylinder at the end, which contained a bolt release mechanism that could be turned by the key. However, the cylinder had barriers or "wards" that prevented the key from turning, if the tab ran into the wards.
The warded lock was an improvement over the key-&-pin lock, but it was still easy to pick. All that was required was a key with a narrow tab on the end, meaning it evaded all the wards. Such a "skeleton key" could, in principle, open any warded lock. It allowed, say, the lord of the manor to get into any room, while guests could only get into their assigned rooms. Presumably, the authorities took a dim view of anyone found carrying a skeleton key who wasn't authorized to do so. Warded locks still linger today, in cheap padlocks and lockboxes. Again, they're easily picked, but it's easy to defeat padlocks and such anyway with the right tools, for example bolt-cutters.
* Lock technologies began to evolve rapidly with the arrival of the Industrial Revolution, with refined lock designs emerging from late in the 18th century. In 1843, Linus Yale SR (1797:1858) patented his "pin and tumbler" lock, now known as the "Yale lock".
The Yale lock features a rotating cylindrical plug in a fixed casing, with a series of holes -- typically five or six -- in the casing and the plug. Each hole contains a spring-loaded pin, each pin being split into a "driver pin" and a "key pin". Each pin assembly is the same length, but the split between the driver and key pins is different for each one. Only when a key raises the pins to the proper height so that the split aligns with the interface between the casing and the plug will the plug be able to turn, pulling the door bolt and opening the door. Linus Yale JR (1821:1868) improved upon the design in 1861, adding the now-universal flat, grooved key design.
The origins of the modern multiple-dial combination lock are obscure, because, as mentioned, the idea goes back at least to Roman times. These days, multiple-dial combination locks persist as bicycle chain locks, briefcase locks, and padlocks. The basic idea is simple, with the lock consisting of a number of disks, typically four, each numbered from 0 to 9 on the rim, rotating around a bolt and spaced along it. Each disk has a slot in it, keyed to a number on its rim. When all four disks are rotated to their proper positions, the bolt is free to move.
The problem with the configuration as described is that it is not possible to change the combination, so in practice the numbers on each disk are on a ring that meshes with the interior disk. When the padlock is open, pressing down on the hasp "floats" the rings off the disks, allowing them to be repositioned without moving the disks. When the hasp is released, the rings re-engage with the disks. As a rule, multiple-dial combination locks are easy to crack -- since with the right handling, it is possible to "feel" when a disk engages a tab. Since padlocks, bicycle locks, and briefcase locks are easily defeated by brute force, that isn't really a problem.

The Yale lock and multi-dial combination locks remain in widespread use today. The single-dial combination lock, which emerged late in the 19th century, also continues in some use, notably on safes, though it's not so common -- this lock using a dial to spin around three (sometimes four) disks with a slot on the edge, the lock opening when the slots on the disks all line up. Each disk has a tab sticking out of the side, with the dial driving a cam with a tab on the front at the rear of the "wheel pack" that catches the first disk when spun around; then the second disk when spun around again; and the third disk when spun around again.
Once all the disks are moving together in the same direction, the user positions the dial to the first number in the combination; then spins the dial around backwards twice, leaving the front disk in place, and then selects the second number in the combination; and finally spins the dial around once, leaving the middle disk in place, to select the third number in the combination, with the rear disk then lined up, to open the safe. The combination can be changed while the safe is opened, using a special tool to "float" the disks to new positions, relative to a new combination.

It was apparently once possible to crack a safe by using a stethoscope to listen for the engagement of the slot on the disks -- it was a meme in old movies -- but that was easily defeated by adding a "clicker" to make a whirring noise as the dial was spun.
Mechanical pushbutton locks were invented in the 1920s, though they didn't catch on until the 1960s, and still remained a secondary technology. Not much documentation is available on how they worked. One obvious approach is to have two-position mechanical toggles, where one position can be "programmed" to OPEN, and the other to CLOSED. Pushing the right set of buttons would result in all OPEN positions, resulting in an unlock. It seems there were more elaborate schemes. These days, digital pushbutton locks are commonplace, for example in gym lockers, since they don't need a key that has to be carried around. However, electronic locks are beyond the scope of this document.
BACK_TO_TOP* Sources include:
Yet another useful source of information was the ENCYCLOPEDIA BRITTANNICA. Their writeup is relatively short, terse, and characteristically dry, but it is extremely concise and provides a nice survey of fundamentals.
A number of websites were consulted as well. John Savard's A CRYPTOGRAPHIC COMPENDIUM is particularly interesting, with many details on various codes, ciphers, and code machines. Another very useful document I found on the Web was a lecture written Anthony E. Sale, the director of the Bletchley Park museum, on the cracking of Lorenz, the development of Colossus, and its reconstruction. The PBS NOVA program web pages on BREAKING THE NAZI CODE TV program have a transcript and also additional details on the Enigma machine. Of course, the NSA museum site has some good information.
The PGP site has a nice little INTRODUCTION TO CRYPTOGRAPHY in PDF format. I thought that after developing my rough notes for this document reading another introductory document might not be very productive, but this file added quite a few little fine points that I incorporated into my text. RSA Laboratories also had a very useful CRYPTOGRAPHY FAQ (Frequently Asked Questions) document. I normally don't have much liking for FAQs, since they're generally just haphazard sets of notes thrown together, but this document was very concise and well-organized, if also basically oriented towards serious crypto addicts.
There are many other cryptologic websites on the net. The HANDBOOK OF CRYPTOLOGY is actually available online in PDF format for anybody who wants a professional-level reference. My attitude towards such formal texts is that they are fine for professionals, but for those not actually intending to do any professional work in a particular field, reading one is usually like digging a tunnel to get to the grocery store -- a great deal of wasted effort yielding little of any usefulness.
* Illustrations credits:
* Revision history:
v1.0 / 01 jan 01 v1.1 / 01 jul 01 / Minor corrections and updates. v2.0.0 / 01 mar 02 / Major update, added CODEBREAKERS material. v2.1.0 / 01 sep 03 / Work begun 10 July 2002. v2.2.0 / 01 jun 04 / Added photos & NSA materials. v2.2.1 / 01 oct 05 / Review & polish. v2.2.2 / 01 dec 06 / Minor changes on odds calculations. v2.2.3 / 01 jan 07 / Correcting a bug or two. v2.2.4 / 01 jan 09 / Review & polish. v2.3.0 / 01 dec 10 / Updates on WW2 crypto, SIPRNet. v2.3.1 / 01 nov 12 / Smart cards & passwords. v2.3.2 / 01 oct 14 / Review & polish. v2.4.0 / 01 sep 16 / Tweaks, rewrite of POLITICS OF CIPHERS section. v3.0.0 / 01 aug 18 / Got rid of POLITICS OF CIPHERS, dropped a chapter. v4.0.0 / 01 jun 20 / Added chapter on contemporary cryptology. v5.0.0 / 01 jan 21 / Added chapter on politics of cryptology. v6.0.0 / 01 aug 21 / Cut out modern cryptology & politics to new documents. v6.0.1 / 01 jul 23 / Review & polish. v6.1.0 / 01 jul 25 / Added mechanical locks, went to 10 chapters.BACK_TO_TOP
