
* One of the properties of matter is that is can support transfers of mechanical energy, whether the matter is solid, liquid, or gas, without any net movement of the molecules involved. Such transfers are referred to as "wave motion", or a transitory displacement of atoms within the matter that passes on kinetic energy. This chapter discusses the physics of mechanical wave motion. Light also involves wave motion, but not of a mechanical sort, and are discussed in the following chapter.
* We're all familiar with wave motion. The sounds that we hear are waves passing through the atmosphere, with the air compressing and decompressing in an oscillating fashion, passing the sound energy outward at hundreds of kilometers per second. We're all familiar with the waves that expand outward after we drop a big rock in a pond, or the waves that we create by whipping a rope tied to a fence up and down.
There are two kinds of waves: "transverse", and "compression" or "longitudinal" waves. In a transverse wave, the molecules move back and forth at a right angle to the direction of motion. A rope being shaken with an up-and-down motion generates a transverse wave, and the ripples we see spreading across a pond are also transverse waves. In a compression wave, the molecules move back and forth in the direction of the wave motion. Sound is a compression wave. A more easily visualized compression wave can be produced by taking a "Slinky" toy, holding it in both hands, and shaking it with a side-to-side motion.
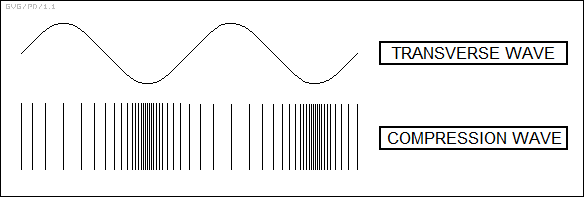
Transverse waves can only arise in a solid medium, or at the interface between a liquid and gaseous medium. A strictly gaseous or liquid medium can only support longitudinal waves.
* Waves have a specific speed of propagation that depends on the matter transmitting the wave, or "wave medium", and the environmental conditions. In dry air at sea level at freezing temperature (zero degrees Celsius), the speed of sound is 331.6 meters per second, or 1,194 KPH.
In reality, the speed of sound is far from constant. For one thing, an increase in temperature increases the speed of sound. For example, at 20 degrees Celsius, the speed of sound increases to 344 meters per second or 1,238 KPH. At higher temperatures, the molecules are moving more quickly and can transmit sound energy more quickly. Moisture in the air also increases the speed of sound, since the water molecules are on the average lighter than the air molecules they replace, and lighter molecules have less inertia and react more quickly. In general terms, then, the speed of sound:
Sounds also generally move much faster in dense liquids and solids than in gases. However, in solids sounds are also dependent on the elasticity of the material, increasing with elasticity. The speed of sound in water is about 1,525 meters per second or 5,490 KPH at normal temperatures, increasing greatly with temperature. Of course, sound is a compression wave, and this is not the same as the velocity of the transverse surface waves that travel across bodies of water, which surfers can "ride" for their amusement. Surfing would not be fun for most people if the speed of such waves was any real percentage of 5,490 KPH. The speed of sound in copper is about 3,353 meters per second or 12,070 KPH at normal temperatures, but oddly decreases with temperature, because the metal's elasticity falls off.
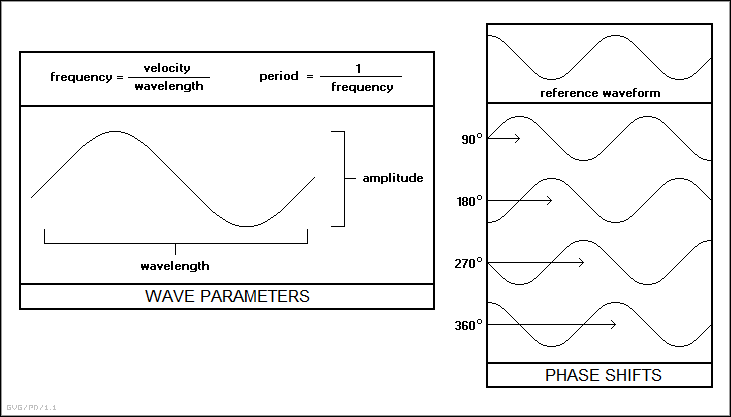
* Waves can have different "amplitudes", or variation in magnitude between "peaks" and "troughs" of the wave, with the power carried by the wave increasing with amplitude. The energy carried in a wave is proportional to the square of the amplitude. It should be noted that in many of the examples of mechanics presented earlier in this document, energy losses were described as due to friction, but that's a bit of an oversimplification; energy is also carried off by sound waves.
Waves can have different spacings, or "wavelengths", between successive regions of maximum density (for a compression wave) or peaks (of a transverse wave). The wavelength is related to the "frequency" of the wave, or the number of times it oscillates in a second while passing through a fixed location, by the simple relationship:
_________________________________________________________________________ frequency = velocity / wavelength _________________________________________________________________________
For example, for a sound wave propagating at 344 meters per second and a wavelength of ten centimeters, the frequency is 3,440 "cycles per second" or, using modern terminology, "hertz (Hz)". For a wavelength of 20 centimeters, the frequency falls to 1,720 Hz.
Waves correspondingly have a "period", which is the time between passages of consecutive crests troughs of the wave. The period is given by the inverse of the frequency:
_________________________________________________________________________ period = 1 / frequency = wavelength / velocity _________________________________________________________________________
Finally, waves have a "phase", in that the peaks of one wave may not coincide in time with the peaks of another wave of the same frequency. Suppose Dexter -- a junior mad scientist -- has two wave tanks, side by side, and generates waves of the same frequency in both. At first the two wave generators are set up to operate in perfect synchronization, but then one is momentarily paused or delayed so that the peaks of its waves don't match up with the other. The two waves are now "out of phase".
Phase is measured in degrees or radians. When the two waves are in phase, they have a "phase difference" of 0 degrees. As one of the generators is delayed so that the phase falls behind that of the other, the phase difference increases. When the two waves are completely out of step or "antiphase", with the peaks of one coinciding with the troughs of the other, the phase difference is 180 degrees. If the generator is delayed again, its wave output will eventually come back into phase with the other, and the "phase shift" will have gone through a full cycle of 360 degrees.
Please remember that phase is a comparative concept. One wave by itself doesn't really have a phase, but multiple waves being compared, or a individual waves compared to a specific reference time, do have phase.
* The most recognizable, and for purposes of mathematical analysis fundamental, form of a wave is a "sine wave", which is produced by the trigonometric sine function. It is the wave which is produced if the position of the tip of a clock hand moving at a steady rate is plotted over time. Given a sine wave of a given amplitude, velocity, and period, then that wave can be represented by the formula:
_________________________________________________________________________ amplitude * SIN( 360 * time / period ) _________________________________________________________________________
-- or equivalently:
amplitude * SIN( 360 * time * frequency ) amplitude * SIN( 360 * time * velocity / wavelength )
If a phase needs to be added, it can be expressed as:
_________________________________________________________________________ amplitude * SIN( 360 * time / period + phase ) _________________________________________________________________________BACK_TO_TOP
* Sound waves are of course important to humans for speech communications and music, and the study of sounds is a domain in its own right, known as "acoustics".
The sounds we hear can be characterized by three parameters: the loudness of the sound, its "pitch", and its "quality". The loudness of the sound obviously depends on the level of energy being pumped into the sound waves, but interestingly our perception of loudness is roughly proportional to the cube root of the energy of that sound. In simpler terms, to make a sound seem twice as loud, we have to pump eight times the energy into it.
The loudness of sounds is measured in a logarithmic scale known as "decibels", defined as ten times the exponent of 10 for the loudness value. The threshold of hearing is defined as 0 decibels. 10 decibels is ten times as loud, while 20 decibels is 100 times as loud, and 30 decibels is 1,000 times as loud. Typical sounds of traffic are about 70 decibels, while the noise of a nearby jetliner is about 140 decibels.
Pitch is simply the frequency of the sound. Somebody who talks in a deep gravel voice has a low-pitched voice, while most children tend to have high-pitched voices. The concept of pitch is of course fundamental to music, with musical "notes" of given frequencies arranged on a musical "scale".
The classical scheme defining a musical scale involves dividing the range of musical tones into "octaves", named because each octave contains the eight whole notes "A", "B", "C", "D", "E", "F", "G", and "A", centered on the "Middle C" note at 264 hertz. Each "octave" of eight notes below Middle C halves the frequency, while each octave above doubles it, as follows:
_______________________ -C''' 33 hertz -C'' 66 hertz -C' 132 hertz MIDDLE C: 264 hertz +C' 528 hertz +C'' 1,056 hertz +C''' 2,112 hertz +C'''' 4,224 hertz _______________________
There are different ways to define the tones in each octave. The most common, for Western music at least, is the "equitonic" scale. Examination of a piano keyboard shows that there are twelve keys in each octave, with seven white keys defining the "whole" notes and five black keys defining "sharp notes" and "flat notes". In the equitonic scale, the ratio from one of the keys to the next is the same for each key. Since an octave means a doubling of frequencies, that means that this interval is the twelfth root of 2, or about 1.05946. The frequency values are rounded off to integers in practice. The following table gives the tones for the first octave above Middle C, with a "#" indicating a sharp note and a "-" indicating a flat note:
______________________ C 262 hertz C# / D- 277 hertz D 294 hertz D# / E- 311 hertz E 330 hertz F 349 hertz F# / G- 370 hertz G 392 hertz G# / A- 415 hertz A 440 hertz A# / B- 466 hertz B 494 hertz C' 524 hertz ______________________
Other scales, such as the more traditional "diatonic" scale, do not use equal intervals, but that makes changing to different keys more troublesome.
The quality of a sound describes the kind of sound we hear, regardless of tone. Most people can distinguish a note played from a piano from a note played from a flute, even if they're the same tone. This intuitively obvious, but not so easy to define in detail.
One of the important aspects of musical quality is the fact that, in general, a musical tone will not consist of a single frequency. This will be true for a simple electronic tone, but if Dexter presses the Middle C key on a piano, it will not only produce a sound with a frequency of 262 hertz, it will also simultaneously produce a range of other sounds of lesser amplitudes and higher frequencies, mostly integer multiples such as 524 hertz and 1,048 hertz. These different sounds are the "components" of the actual tone. The basic and most significant component of the tone, in this case 262 hertz, is called the "fundamental", while the component at the higher frequencies are called "harmonics". The set of these sounds is referred to as an "audio spectrum".
Different instruments generate different audio spectra for the same tone, which is one reason they sound distinct. There are other features to the quality of a musical tone, but further discussion would be leaving the domain of physics and crossing over into musical theory.
* The human ear can hear tones up to about 20 kilohertz. Most sounds in speech are below 3 kilohertz, so most telephones and voice radios only transmit sounds up to 3,000 kilohertz. Although, as the table above shows, musical tones don't go above about 5 kilohertz in themselves, loss of high frequency harmonics tends to make music sound muddy, and so "high-fidelity" systems need to produce sounds including frequencies of up to 16 kilohertz or better.
Some audio enthusiasts claim they can hear distinctions in sounds with tones above 20 kilohertz, but such claims are rarely validated by "double blind" tests, where neither the subject nor the person administering the test knows what the frequency makeup of the sounds are supposed to be. A few of the most earnest enthusiasts have responded to such negative results by attacking the validity of double-blind tests, but so far their arguments have not carried the day.
Some animals can hear well above the human range of hearing. For example, bats, whales, and dolphins have a hearing range much wider than that of humans. These animals use their vocalizations to perform ranging and location. They emit high-pitched sounds and then listen for echoes bounced off a target. The longer the interval between producing the sound and the return of its echo, the farther the target, and these animals also have ear structures that allow them to determine the direction of the echo. Humans developed an electronic approach to the same procedure after the First World War to hunt submarines, ultimately naming the scheme "sonar", for "sound navigation and ranging".
BACK_TO_TOP* If a sound wave propagates through the air and runs perpendicularly into a flat, hard wall, it bounces off the wall and returns back in the direction it came from. This process is referred to as "reflection", and of course we recognize this as an echo.
This is the simplest scenario of a reflection, and in the real world it's a bit more complicated. First, if the flat wall is at an angle to the direction of the propagation of the sound, the sound will be reflected away at the same angle relative to the wall. For example, if the wall is at an angle of 45 degrees to the direction of propagation of the sound wave, the reflection will be at an angle of 45 degrees relative to the wall, or 90 degrees relative to the original direction of the sound. If the wall is made up of many different elements at many different angles relative to the propagation of the sound wave, it will generate reflections in many different directions, scattering the sound wave.
Not all the energy of the sound wave will be reflected from the wall; some of it will be absorbed by the wall as well. This combination of reflection and transmission will actually happen any time a sound wave makes a transition from one distinct acoustic medium to another, or in other words propagates through a "discontinuity".
* Another interesting phenomenon occurs when the wavefronts of a sound wave pass through a discontinuity at an angle. The wave will have different velocities in the different media separated by the discontinuity, and the portions of the wave that are propagating through the second medium do not travel at the same rate as those arriving from the first medium. This means that the direction of propagation of the wave in the second medium will be shifted from that of the first. This property is known as "refraction".
Yet another property of waves is their ability to flow around the edges of barriers. While a solid wall will block sound or water waves hitting it from one side, they will still slop around the edges of the walls, though their energy will be much diminished. This phenomenon is known as "diffraction". Neither refraction nor diffraction are all that important in the study of sound waves, but they are of great interest in the study of light waves, as discussed in the next chapter.
* If two waves of the same wavelength and amplitude travel through the same medium at the same velocity but in opposite directions, they set up "standing waves". The best-known example of this is that of a rope tied to a post. If Dexter shakes the rope up and down, the wave travels down the rope, hits the post, and then reflects back at him.
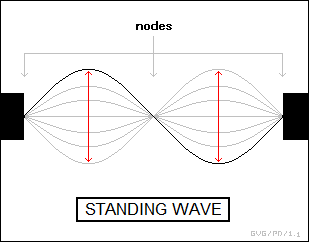
Dexter can time his shakes to synchronize in phase with the reflections so that fixed sections of the rope oscillate up and down, with the boundaries between the sections remaining effectively stationary. This is known as a "standing wave", as opposed to "traveling waves", or waves in normal unconstrained propagation. A standing wave actually consists of a superposition of two waves, one propagating in one direction and its reflection propagating back in the other direction. The stationary points on the wave are referred to as "nodes".

The standing waves on the rope will always be multiples of a half-wavelength to ensure synchronization between the input wave and the reflected wave. The standing wave with a half-wavelength will have one node at each end and will move up and down in between; the standing wave with a full wavelength will have a node in the middle; the standing wave with 1.5 wavelengths will have two nodes in the middle; and so on. A plucked string on a musical instrument, such as a guitar, sets up standing waves.
Similarly, a police whistle generates standing waves with the wavelength given by the size of the whistle -- the smaller the whistle, the shorter the wavelength and the sharper the tone. The whistle acts as a "resonant chamber" or "resonant cavity" that selectively produces that tone from the air blown through it by the policeman. There is generally a little ball in the chamber of the police whistle, which interferes with the resonance and breaks up the whistling tone, making it more obnoxious; without the ball, a continuous whistling tone is generated.
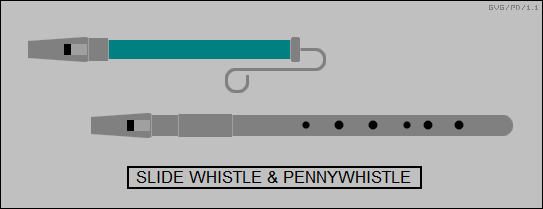
A slide whistle allows the player to vary the tone continuously by moving a rod connected to a plug that varies the size of the resonant chamber. It is also possible to alter the resonant characteristics of a whistle by placing holes in the whistle tube, which the player can cover and uncover with his fingertips; such whistles include the classic Irish "pennywhistle" or "tin whistle", and the more traditional "recorder". Incidentally, pennywhistles and recorders are not technically referred to as "flutes". In a flute, the player blows across the top of a hole to generate the basic tones, instead of blowing straight through the instrument.
BACK_TO_TOP* The motion of a source emitting a wave affects the frequency of that wave. This phenomenon is known as the "Doppler effect". The most popular example of the Doppler shift is the sound of a moving train. If a train approaching at high speed blows a whistle, the frequency of the whistle is higher than it would be if the train were at rest. Similarly, if the train is moving away, the frequency of the whistle is lower.
This is easy to see mathematically. Suppose we designate the speed of sound as S and the velocity of an approaching train as V. Suppose the train is emitting a very short sharp blast on its whistle on an interval given by time T. If the approaching train emits a blast at time 0, then by the time it emits its second blast at time T, it will have moved closer by the distance V * T, and the sound of the second blast will not have to travel as far as the sound of the first.
The amount of decrease in the measured blast period will be given by the ratio of the train's velocity to the speed of sound. For example, suppose the blast period T is one second. If the train's velocity V is a tenth of the speed of sound, then in one second it will travel a tenth as far as sound does in one second, and the measured blast period Tm will be reduced to 0.9 seconds.
In more general terms:
Tm = T * ( 1 - V/S )
In sum, the blast period observed from a moving train to the blast period observed from the stationary train is then:
_________________________________________________________________________ Tm = T * ( 1 - fraction_soundspeed ) _________________________________________________________________________
If the train is moving away, the minus sign is changed to a plus, and the blast period is increased:
_________________________________________________________________________ Tm = T * ( 1 + fraction_soundspeed ) _________________________________________________________________________
The blast frequency will be the inverse of the blast period.
This analysis applies to continuous waveforms as well. Suppose the train was also emitting a low-frequency audio signal in the form of a sine wave, and the blast was synchronized so that it was emitted at the beginning of each sine cycle. Clearly the two signals will remain in lockstep, and the sine wave will be Doppler-shifted exactly as the blast is.
BACK_TO_TOP* One of the interesting features of waves is that their interactions are additive. For example, suppose Dexter generates two water waves of the same frequency and amplitude, and have them meet head on. When two peaks pass through the same point, the amplitude of the peak will be doubled. When a peak and a trough match up, they cancel out or "interfere".
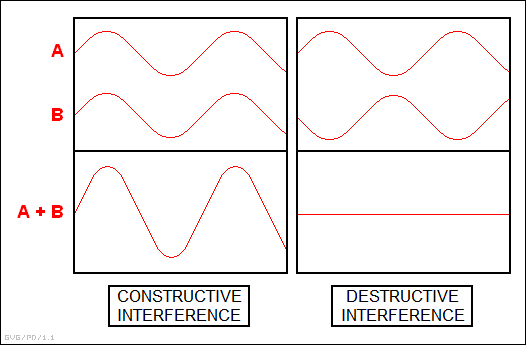
An interesting example of interference at work is to produce two sound waves of frequencies that are almost, but not quite, the same. As the two sounds move in and out of phase, they will eerily grow louder and quieter on a regular cycle. This is known as a "beat", though it has little to do with the "beats" that time musical compositions.
Suppose Dexter generates two sounds, one at a frequency of 300 hertz and the other at a frequency of 302 hertz. This means that they will both complete an integer number of cycles -- 150 and 151 respectively -- every half a second, and so the sound will vary in volume through a full cycle twice a second. The actual frequency of the sound heard will be 301 hertz.
Wave interference is the basis of "active noise cancellation" systems. These systems include three elements: a microphone, a processor, and loudspeakers. The microphone samples external sounds and feeds them to the processor, which then calculates how to drive an antiphase signal to the loudspeakers that cancels out the external sound. Of course, this works best when the sounds are regular and predictable, for example the constant rumble of a large ventilation fan, or a vehicle going down the road.
It may be cheaper to fit a vehicle with an active noise cancellation system than to provide soundproofing, and it will also extend the vehicle's life by damping out vibrations. Active noise cancellation is also now found in high-end earphones, the earphones having microphones and "smarts" to alter the audio being played to cancel out external sounds.
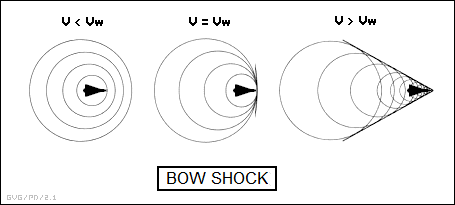
* One of the interesting implications of constructive interference is the concept of "bow shock". Suppose Dexter is at the helm of a boat sitting still on water. If he moves around in the boat, the rocking of the boat sets up ripples in the water that travel in a circle, radiating outward from the boat.
Now suppose Dexter starts driving the boat forward; it then sets up a continuous series of waves that propagate circularly from every point that the boat moves through. If the boat is moving slower than the speed of the waves, this creates a Doppler shift, with the wavelength compressed in front of the boat and expanded behind the boat.
The interesting thing is what happens when the boat exceeds the speed of the waves in water. All the waves in the front of the boat merge together, leaving behind a high-amplitude, vee-shaped bow shock wave behind the boat. Water skiers are very familiar with this bow shock wave, since they like to hop over it or even surf on it for a while. The angle of the vee grows narrower as the speed of the boat increases.
Supersonic aircraft also produce a bow shock wave that results in the propagation of an abrupt high-pressure wave in a conical footprint under the aircraft's flight path, causing a "sonic boom" that can rattle windows. Such sonic booms were common in the late 1950s and the 1960s, before the complaints of the citizenry forced the military to impose more stringent flight rules on their pilots. Incidentally, large aircraft moving out at supersonic speeds at very low altitude could leave a massive trail of destruction in their wake, but the military never formally used such a technique in combat because it was so indiscriminate.
* It was mentioned earlier in this chapter that musical instruments normally generate a spectrum of sound frequencies for each musical note. The fact that waves are additive means that all these "component" sounds, consisting of nice clean sine waves, actually constitute a single, messy-looking sound waveform.
This seems puzzling at first, since it leads to the question: which is for real? The spectrum of component sounds? Or the single messy-looking sound waveform? The answer is: they both are. The tone could be interpreted in either way, depending on which is more convenient to the task at hand.
A branch of applied mathematics known as "Fourier analysis" has been developed to translate between the two aspects of the sound, as well as other, similar wave phenomena. The sound can be inspected either in the "frequency domain", in the form of a spectrum of simple sine waves, or in the "time domain", in the form of a messy single waveform. Further discussion of Fourier analysis is far beyond the scope of this document.
BACK_TO_TOP* We have already discussed how sound can be created from a vibrating string or from a resonant chamber, such as a whistle. This is related to the concept of "structural resonance", or the notion that structures tend to oscillate at certain specific frequencies when subjected to forces. The most common example is that of a set of wind chimes. If one of the chimes is struck, it vibrates at a certain frequency, and this frequency increases for smaller chimes, since they can vibrate more rapidly.
Another example of mechanical resonance that was of great practical use for centuries is the "pendulum", the swinging weight on a rod that times a grandfather clock. The weight on the end of the pendulum swings back and forth, with maximum kinetic energy and speed at the bottom of its arc and maximum potential energy as it momentarily halts and reverses direction at the ends of its arc.
Although a detailed analysis of pendulum motion is beyond the scope of this document, very interestingly in principle the period of a pendulum only depends on the acceleration of gravity and the length of the rod as follows:
_________________________________________________________________________ period = 2PI * SQRT ( acceleration_of_gravity / length_of_rod ) _________________________________________________________________________
This neat property, which was discovered by Galileo, allows a pendulum to count the ticks of a clock, an application that was invented by Christiaan Huygens. Since there are always some friction losses in the operation of the clock that cause it to run down, the clock includes a mechanism, either driven by a coiled "mainspring" or a weight falling on a chain, to provide a little force that keeps the pendulum in motion, while the pendulum keeps the mechanism operating at predictable rate. The mechanism links to the pendulum through a gear wheel with jagged teeth known as an "escapement wheel"; and the pendulum links to the escapement wheel through a "pivot", a pivoting arm with two teeth that rocks back and forth in step with the pendulum. The force of the teeth of the escapement wheel against the teeth of the pivot keeps the pendulum in motion, while the back-and-forth motion of the pivot keeps the teeth of the escapement wheel stepping at a fixed rate, providing the "tick-tock" as the clock counted off the seconds.
Since the length of the pendulum rod tends to change with temperature from summer to winter, precision pendulum clocks were once made that had rods assembled from segments of dissimilar metals so their length would remain more constant. Much effort and ingenuity was put into developing highly accurate pendulum clocks. One of the indications of their accuracy was that when clocks were moved from high latitudes to equatorial regions, their timing clearly seemed to run faster. As it turned out, the equatorial bulge of the Earth means that the acceleration of gravity is very slightly less than it is at high latitudes, resulting in a slightly but shorter pendulum period that became obvious over relatively long periods of time.
* Pendulums are very simple systems, but they illustrate several concepts in basic physics. For example, if the travel of a pendulum is charted over time, it will create a neat sine curve. Another interesting aspect of the physics of the pendulum is that it can be used to demonstrate the rotation of the Earth as a simple consequence of the First Law of Motion.
If a pendulum is made of a weight hung from a wire so that it can swing back and forth in any direction in the horizontal plane, then if the pendulum is placed at the North or South Pole, its direction of motion will remain unchanged as the Earth spins beneath it, or from an observer's point of view the direction of its swing will pivot around in a full circle every 24 hours.

If such a "Foucault pendulum" is taken to lower latitudes, the time required for it to shift its direction of swing will increase. At the equator, its direction of swing will not change at all, because then the change in the Earth's direction is in the pendulum's vertical plane, not its horizontal plane. Large Foucault pendulums are often displayed in science museums, at least at high latitudes. However, this is drifting away from the topic of mechanical resonance.
* There is another variation on the basic pendulum, called a "torsional pendulum", which involves a weight spinning at the end of a wire, twisting up the wire until the weight comes to a halt and then reverses direction. Analysis of a torsional pendulum is a little more complicated than that of a normal swinging pendulum, but the period of a torsional pendulum is also relatively constant, and it has also been used as a timekeeping element of clocks.
Since including a swinging pendulum on a small portable desktop clock or clockwork watch wasn't practical, clockmakers developed a variation on the torsional pendulum, known as the "hairspring". This is a loosely coiled spiral of metal placed inside a relatively massive ring known as a "balance wheel"; the inner end of the hairspring is attached to a fixed axle, while the other end is connected to the interior of the balance wheel. The balance wheel is set to spinning one way, tightening up the hairspring, and then the hairspring unwinds to send the balance wheel in the other direction, with the cycle repeating over and over at a constant rate. The period of the hairspring could be "tuned" with a moveable arm that limited the maximum radius of its extension.

For a desktop clock, the position of the hairspring wasn't critical, but for watches, which move around a good deal, it was placed at the center of the watch to make sure the external forces on it were as neutral as possible to keep from affecting the assembly's period. As with the swinging pendulum, both the torsional pendulum and the hairspring assembly interface to the rest of the clock through a pivot and escapement wheel.
* Yet another variation on the pendulum is a bobbing pendulum, consisting of a weight attached to a spring, bobbing up and down. Since the motion of this pendulum tends to run down quickly, this scheme is not used much or at all in clocks or other machines, but the mathematical analysis of such a system is straightforward, and it is used as a tool in teaching the theory behind mechanical resonance.
Since an idealized spring has no losses, a third element called a "dashpot" is added to incorporate losses into the system. Analysis of such a "spring-mass-dashpot" system is yet another thing beyond the scope of this document, though it will be quickly encountered by readers who go on to college-level basic physics or engineering courses.
* Machines or buildings can have unintended and unwanted structural resonances. One of the items in the test program for products such as computers or power tools is to put them on a "vibration table" and see how well they stand up to vibration, and particularly to see if there are certain resonant frequencies where they vibrate all too well and shake themselves to pieces. One of the elements in aircraft flight test programs is to identify flight conditions in which the wings or other elements of the machine will oscillate, or "flutter", possibly leading to loss of control or damage to the aircraft.
Skyscrapers tend to sway slightly in high winds, acting as inverted pendulums fixed to the ground, and will oscillate back and forth with a resonant period of several seconds. Under certain wind conditions, such oscillation could be a threat to the building, since the motions could build up, like a kid "pumping up" a playground swing, until they bring the house down.
The most famous example of destructive structural resonance occurred on 7 November 1940. The Tacoma Narrows Bridge, a new 850-meter-long, slender suspension bridge in the northwest US state of Washington, proved to oscillate so badly in crosswinds that it was nicknamed "Galloping Gertie". When the structure was hit with a steady 68 KPH wind on that day, it began to oscillate at its resonant frequency, the wind twisting the roadbed one way and then the other as it turned up and down, and collapsed a little over an hour later. The only casualty was a dog, but in the aftermath of the accident, some other suspension bridges were reinforced to damp out such oscillations. The bridge was rebuilt a decade later in a more robust form.
The Citicorp skyscraper in New York City incorporates an "oscillation damper" at its top to reduce its sway and damp out oscillation. The damper consists of a 365 tonne concrete slab that is moved back and forth under control of motion sensors attached to the building's structure. If the building begins to sway one way, the slab is shifted in the other direction to compensate. Implementing the damper was cheaper than adding wind bracing to the building's structure.
It is also possible in principle to build dampers using water tanks, with large tanks at the four sides of the top of the building and cross-connected by pipes at the bottoms of the tanks. Under normal circumstances, the water level will be the same in all tanks, but if the building sways, the sway will cause the water to slosh through the pipes. The tank system is designed so that its own resonant frequency is the same as that of the building but lags the sway, with the antiphase resonances of the building and the tank system tending to cancel each other out.
BACK_TO_TOP