
* The 20th century saw the development of quantum physics, which explained the internal structure of atoms. This knowledge gave chemists the tools to finally understand the actual basis for the rules of chemistry, as well as new tools to exploit.

* In the last decades of the 19th century and the first few decades of the 20th century, physicists made a series of discoveries that would have a profound effect on chemistry. From 1879, the British physicist William Crookes (1832:1919) had conducted studies of faint glows in "discharge tubes", glass tubes through which an electric current was conducted. They gave off a faint, mysterious glow that would turn out to be due to interactions between the electricity flowing through the tubes and residual gas in them.
In 1897, the British physicist Sir Joseph John "J.J." Thomson (1856:1940) of Cambridge University in the UK was able to show that the electric current in a "cathode ray tube", an improved derivative of Crookes' tube, was in the form of negatively charged particles, which became known as "electrons". They were clearly smaller than atoms, though their actual size wouldn't be precisely determined for two more decades. This was the first step towards understanding that the atom had an internal structure and was not indivisible, as had been assumed.
Now Arrhenius's ideas about ionic dissociation began to make more sense: an atom could become negatively charged by gaining an electron, or positively charged by losing one. An atom could be "multiply ionized" by losing or gaining more than one electron. In modern terms, "Na+" is sodium ionized by losing one electron; "Cl-" is chlorine ionized by gaining one electron; Fe2+ is iron ionized by losing two electrons; and "Fe3+" is iron ionized by losing three electrons.
* Other evidence was beginning to accumulate at the time that the atom was not as simple and fundamental as had been supposed. In 1895, the German researcher Wilhelm Conrad Roentgen (1845:1923) discovered that a cathode ray tube emitted an invisible form of radiation that could penetrate through soft materials but not hard materials. He called it "X radiation" because he didn't know what it was, though it would later prove to be high-energy electromagnetic radiation.
Roentgen won the 1901 Nobel Prize in physics for his discovery. Although he didn't know what X-rays really were, he did know that they could sleet right through the body onto a photographic plate, leaving "shadows" of the heavier bones on the image. The first formal X-ray photograph was of the hand of Roentgen's wife Bertha, showing the bones in her hand and her wedding ring. X-rays were quickly applied to medical imaging to check broken bones and the like, and in fact they became something of a public fad for a time, with X-ray images taken as carnival attractions and people worrying about snoopers using X-rays to peep into houses.
In 1896, the French physicist Anton Henri Becquerel (1852:1908), having heard about Roentgen's discovery of X-rays, wondered if phosphorescent materials also emitted invisible radiation. Becquerel performed experiments with photographic plates that almost accidentally showed that some materials emitted an invisible form of radiation spontaneously. Becquerel had discovered "radioactivity", though he only knew that it happened and had little concept of the details, thinking that the radiation was in the form of X-rays.
Two French chemists, the husband and wife team of Pierre Curie (1859:1906) and Polish-born Marie Curie (1867:1934), were able to demonstrate that radioactivity was a property of atoms. They investigated an ore known as "pitchblende" that was more radioactive than the uranium salts studied by Becquerel and isolated two radioactive elements, "polonium" (named in honor of Poland) and "radium". Radium was about a million times more radioactive than uranyl sulfate. More radioactive materials were quickly discovered by others. Becquerel and the Curies would share the 1903 Nobel Prize in physics for the discovery of radioactivity.
In 1897:1898, the New Zealander physicist Ernest Rutherford (1871:1937), working in J.J. Thomson's Cavendish laboratory at Cambridge, was performing experiments on radioactive materials and discovered that his samples emitted two types of radiation -- one that was easily blocked, which he called "alpha" radiation, and one that wasn't so easily blocked, which he called "beta" radiation. The alpha particles turned out to be helium atoms stripped of electrons, and beta particles turned out to be electrons themselves. Other researchers discovered a third form of radiation, known as "gamma" radiation, which was a form of electromagnetic energy even more energetic than X-rays.
In 1900, Rutherford, then working at McGill University in Canada, made a really startling discovery: an element that emitted radiation could become another, lighter element. In the case he was investigating, a radioactive element named thorium "decayed" to radium, which in turn decayed to a radioactive gas named "radium". Atoms were not unchanging as had been assumed. Rutherford's work won him the Nobel Prize in 1908.
* One of the problems in advancing the idea of atomic structure at that time was that there were still some scientists, generally physicists, who refused to believe in the existence of atoms. In 1905, the great German-American physicist Albert Einstein (1879:1955) published a set of three memorable scientific papers.
The first of the three papers was on "Brownian motion", the random motions of small particles in water as seen under a microscope and first described by the Scots botanist Robert Brown (1773:1858) in 1827. A Swedish chemist named Theodor Svedberg (1884:1971) had suggested in 1902 that Brownian motion might be caused by the random vibrations of water molecules on all sides of the particle, but Einstein did all the math to show precisely what was going on. Einstein's paper provided an analysis that predicted the effects of Brownian motion could be neatly described by atomic theory. Over the next few years, the French physicist Jean-Baptiste Perrin (1870:1942) did the heavy experimental lifting to demonstrate the validity of Einstein's theory, observing the motions of powdered gum resin in water. He published his results in 1913, showing they matched Einstein's predictions; from that time on, nobody seriously opposed atomic theory. Perrin won the Nobel Prize in physics in 1926 for his work.
The other two papers Einstein published in 1905 would not be as important to chemistry, but they would be very important in the development of modern physics:
The validation of the existence of the atom came at the time when the atom was discovered to have an internal structure. J.J. Thomson had speculated that the atom was something like a positively-charged sphere in which electrons were embedded. This became known as the "plum pudding" model of the atom. However, in 1910 Rutherford, now back in the UK, and his assistants bombarded a gold foil with alpha particles to see how much they were deflected by collisions with atoms. They should have been only slightly deflected, but in some cases they bounced straight back, very much to Rutherford's surprise. He concluded that atoms consisted of a small, dense, positively charged "nucleus" surrounded by orbiting electrons. In 1919, Rutherford was able to determine that the nucleus contained positively charged particles, eventually determined to be 1,836 times as massive as the electron, that he called "protons". A normal hydrogen atom had a single proton for a nucleus, orbited by a single electron.
The order of the elements in the periodic table turned out to reflect their number of protons. Hydrogen, the first in the table, had one proton; helium, the next in the table, had two; lithium three; beryllium four; boron five; carbon six; and so on. The number of protons in an atom is now known as the "atomic number". There was still a puzzle in that the atomic masses of atoms were greater than the number of protons in the nucleus: while hydrogen's mass was about that of a proton, helium's was about four times greater, and carbon's was about twelve times greater. For lighter elements, the ratio of total nuclear mass in proton units versus the number of protons was 2:1, but that ratio tended to creep up incrementally for heavier elements.
Rutherford suspected the additional mass was in the form of neutral particles about the same size as the proton. Neutral particles are harder to detect than charged particles, and so it wasn't until 1933 that James Chadwick (1891:1974), a student of Rutherford's, discovered the neutral particle, known as the "neutron". That meant that the nucleus of atoms generally consisted of protons and a matching or greater number of neutrons; the two particles were lumped together with the term "nucleon". Chadwick won the Nobel Prize in 1935 for his discovery of the neutron.
BACK_TO_TOP* There was a serious problem with Ernest Rutherford's nuclear model of the atom: it proposed that an atom consisted of a positively charged nucleus surrounded by negatively charged orbiting electrons. However, unlike charges attract, and so the electrons should have immediately spiraled into the nucleus. A Danish physicist named Niels Bohr (1885:1962) who was working in Rutherford's lab came up with a solution of sorts in a paper published in 1913. Bohr proposed that electrons orbiting the nucleus of an atom could not occupy just any orbit, they could only occupy certain specific orbits, which he called "stationary states". A photon could make an electron jump from one state to a higher energy state, and it might emit a photon in a high state and fall back to a lower state. The different electron "orbitals" of the atom had specific energy levels, and a transition from one specific orbital to another corresponded to a photon of a specific energy or wavelength. This explained why different atoms had such specific spectroscopic patterns.
The Bohr model of the atom would win him the Nobel Prize for physics in 1922, but it was really just a set of ad hoc assumptions. Why did atoms have these specific discrete orbitals? Just because? Or was there a method to the madness? And the Bohr atomic model didn't really give the right results for anything but the hydrogen atom.
In 1923, a French nobleman working on his doctorate named Duke Louis Victor de Broglie (1892:1987) -- the name is pronounced "debroy" and rhymes, implying no irony, with "destroy" -- came up with an expansion of Einstein's notion of light as particles, photons, with wavelengths inversely proportional to their energies. De Broglie suggested that all particles had wavelengths inversely proportional to their mass, which by Einstein's E = M * C^2 was equivalent to their energies.
One of the implications of this postulate was that it explained the stationary states of atomic electron orbitals. If electrons had a wavelength, then they could only exist in orbits whose circumference was an integer multiple of the electron wavelength, or in other words corresponded to electron "standing waves". That general idea was fleshed out by two physicists in the mid-1920s. The first, a German physicist named Werner Heisenberg (1901:1976) came up with a model of the atom where the orbitals were simply represented by values in a grid or "matrix" of orbital parameters. Heisenberg's "matrix mechanics" avoided the excess baggage of a model that proposed to visualize the internal workings of the atom -- when there was nothing there that we could actually see.
The second, an Austrian physicist named Erwin Schroedinger (1887:1961), came up with an extension of classical wave theory that applied de Broglie's notions of particles as waves to construct mathematical models of atoms. The "Schroedinger equation" seemed to provide a more intuitive model of the atom than Heisenberg's abstract matrix mechanics, and in fact it would prove more popular.
However, it turned out that the two approaches were actually equivalent. Furthermore, Schroedinger had failed to appreciate the fact that combining notions of particle and wave was convenient, but didn't clarify matters all that much. A wave was, in terms of classical physics, a disturbance of a propagating medium, but there was no such medium for the "wavefunctions" described by applications of the Schroedinger equation. The interpretation of the wavefunction would prove very troublesome, and in fact it is still a matter of debate. The details are a distraction in a document on chemistry; the simplest thing that can be said is that the wavefunction -- or more precisely, the square of the wavefunction -- gives a probability distribution for detecting an electron in a specific experiment, and is not really a wave as understood in classical physics.
Describing the atom using the Schroedinger equation required use of another theoretical construct, provided by a Swiss physicist named Wolfgang Pauli (1900:1958). Particles, it was determined, had a property called "spin" that was something like the spin of a ball, but not quite, since it was restricted to specific values: 0, 1/2, 1, 3/2, 2, and so on. Particles that had "integer spin" -- 0, 1, 2, and so on -- had different properties from those that had "half spin" -- 1/2, 3/2, and so on. Given a system of particles, those that had integer spin could all share the same energy state; while those that had half spin could never share the same energy state.
The law that half-spin particles in a system couldn't have the same energy state became known as the "Pauli exclusion principle", and it was very important for chemistry. The electron had a spin of 1/2, and so it obeyed the exclusion principle: simply put, each electron in an atom had to occupy its own orbital, meaning that electrons in a multi-electron atom occupied one of a series of orbitals of increasing energy. This is oversimplifying it a bit, since the electron can have either a spin of 1/2 or -1/2 -- the two values sometimes being referred to as spin UP or spin DOWN -- and one orbital could actually accommodate two electrons of opposed spin. Analysis of atomic orbitals using the Schroedinger equation and the exclusion principle showed that the electron orbitals were organized into sets or "shells".
Pauli, incidentally, provided a memorable contribution to the intermittent war between physicists and chemists. He married a dancer, but she quickly divorced him to go off with a chemist. He commented in disgust: "If she had taken a bullfighter, I could have understood, but a chemist ..."
BACK_TO_TOP* While the quantum theory was evolving, in 1913 one of Rutherford's students, Frederick Soddy (1877:1956) had shown that there were different forms, or "isotopes", of the same sort of atoms. Soddy observed that there were some forms of uranium that were much more radioactive than others, even though all the forms were essentially identical in their chemical properties. Soddy won the Nobel Prize in 1921 for this discovery.
As it turned out, isotopes shared a common atomic number but had different atomic weights. A relatively straightforward means of separating isotopes, known as a "mass spectrograph", was developed by the British chemist Francis William Aston (1877:1945), one of J.J. Thomson's students, in 1919. In the mass spectrograph, atoms are ionized, accelerated by an electric field, passed through a magnetic field that causes them to curve, to finally strike a target containing a set of detectors in a row. The curvature of the ions in the magnetic field decreases with their masses and so different isotopes will fall into different detectors. Aston won the Nobel Prize for chemistry in 1922; over the next two decades, he would sort out over two-thirds of the 282 naturally-occurring isotopes.
The discovery of isotopes immediately showed why William Prout's suggestion a century earlier that the elements were composites of hydrogen atoms hadn't worked out: the atomic weights being obtained at that time were of averages of isotopes. Why an element had isotopes with different atomic weights was a puzzle that wasn't completely resolved until Chadwick discovered the neutron. All the isotopes of a particular element had the same number of protons, but they had different numbers of neutrons. Uranium, for example, had an atomic number of 92, but had two primary isotopes, one with an atomic weight of 238 and another with an atomic weight of 235. These can be shorthanded as "U<238/92>" -- with the "238" read as a superscript and the "92" read as a subscript -- and "U<235/92>". The primary isotopes for common elements include:
__________________________ hydrogen H<1/1> helium He<4/2> carbon C<12/6> nitrogen N<14/7> oxygen O<16/8> sodium Na<23/11> aluminum Al<27/13> silicon Si<28/14> phosphorus P<31/15> sulfur S<32/16> chlorine Cl<35/17> potassium K<39/19> calcium Ca<40/20> iron Fe<56/26> nickel Ni<59/28> copper Cu<64/29> zinc Zn<65/30> silver Ag<108/47> tin Sn<120/50> gold Au<197/79> mercury Hg<200/80> lead Pb<207/82> __________________________
Some isotopes were unstable and radioactive, emitting particles and changing into other isotopes or elements. For example, hydrogen has three isotopes, including H<1/1>, H<2/1> (deuterium), and H<3/1> (tritium), with tritium being unstable, breaking down into He<3/2>. There are elements, particularly those at the upper end of the periodic table, that have no stable isotopes.
Cataloging of isotopes led to a better understanding of the behavior of radioactive decay. Although it was impossible to predict when a single atom of a radioactive isotope would decay, it was possible to predict the decay time of a large assemblage of such isotopes on a statistical basis. Each isotope had its own "half-life", which was the time it would take half of a mass of such isotopes to decay to some other element. A second half-life later, half of the remainder would decay, meaning one quarter was left; decaying to one-eighth in the third half-life; to one-sixteenth in the fourth half-life; and so on.
Entire "radioactive series" were determined which mapped out how one radioactive isotope decayed into another, which decayed into a third, and so on until a stable element was reached. Methods of analysis were developed in which samples of minerals could be dated by their concentrations of various elements in known radioactive series decay chains, providing the first reasonably accurate estimates of the age of the Earth. Radioactive materials also proved extremely valuable in chemical analysis, with specific radioactive isotopes introduced into complicated chemical reactions to allow the steps of these reactions to be followed. Such "radioactive tracers" proved particularly important in biochemistry.
* Radioactive decay turned out to be due to two previously unknown forces. The fact that the nucleus was composed of positively-charged protons and neutral neutrons was puzzling, since the electrostatic repulsion of the protons from each other would seem to drive the nucleus apart. Obviously there was some other force counterbalancing the electromagnetic force in the nucleus, with this force simply known as the "strong force".
The strong force turned out to be about a hundred times stronger than the electromagnetic force. However, the strong force was only effective between neighboring nucleons, while the electromagnetic force was effective through the entire nucleus. That was why no naturally-occurring elements were known that had an atomic weight more than a hundred, since as that point was reached the long-range "couplings" of the electromagnetic force overwhelmed the short-range couplings of the strong force. It was also why elements tended to become more unstable as their atomic number increased beyond a certain limit, and why heavier elements had an increasingly higher ratio of neutrons to protons in their nuclei: adding neutrons increased the strong force couplings without increasing the electromagnetic couplings, making for a stronger nucleus. The struggle between the electromagnetic and strong forces helped explain the process of "alpha decay", in which a nucleus of an atom emitted an alpha particle -- with two protons and two neutrons, exactly the same as a helium nucleus -- which dropped the atom's atomic number by two and atomic mass by four.
Another force, a "weak force", was also found whose behavior was very subtle. Its primary action in radioactive decay was "beta decay", in which a neutron decayed into a proton and emitted an electron, or beta particle. This increased the atomic number by one while leaving the atomic mass the same.
* The discovery of isotopes may have justified Prout's speculations, but it also created a difficulty that would take decades to resolve. Although chemists had performed exacting measurements on atomic weights, with the discovery of isotopes they realized they had only obtained an average value for all the different isotopes found in nature.
Traditionally, as noted earlier, oxygen was assigned an arbitrary atomic weight of 16 as a reference -- but in reality, an ordinary sample of oxygen consisted of three isotopes, the bulk (99.76%) being O<16/8>, but with about 0.2% being O<18/8> and about 0.04% being O<17/8>. Physicists preferred to set the reference weight of 16 to O<16/8> exclusively; that meant that chemists and physicists had two very similar but slightly different lists of atomic weights, one a "chemical" atomic weight and the other a "physical" atomic weight.
That led to a nagging quarrel between chemists and physicists that was finally resolved by an edict published in 1961 by the International Union of Pure & Applied Chemistry, which has standing in both communities. The solution was to adopt a new standard in which C<12/6> was assigned the reference weight of 12. The new system was based on a single isotope, one whose mass was very well known, which pleased the physicists; the chemists liked the new scheme because in the old chemical scale, the chemical atomic weight of carbon had been extremely close to 12 anyway, meaning that the new combined scale was very close to the old chemical scale.
BACK_TO_TOP* In 1916, not long after Bohr introduced his simple atomic model, and well before quantum physics and nuclear research provided a much more useful model, two American chemists, Gilbert Newton Lewis (1875:1946) and Irving Langmuir (1881:1957), came up with what amounted to a "prototype" for a modern model of chemical bonding.
They were following up a suggestion published in 1904 by the German chemist Richard Abegg (1869:1910). With the discovery of the electron, Abegg was able to notice a particular pattern in the number of electrons found in the atoms of the inert gases: helium had two electrons; neon had 2 + 8 = 10 electrons; and argon had 2 + 8 + 8 = 18 electrons. These seemed to be "magic" electron configurations.
What was more interesting was that elements that had one more or less electron than these magic numbers had a valence of 1 and were highly reactive. For example, helium was "bracketed" in this way in the periodic table by hydrogen and lithium; neon by fluorine and sodium; and argon by chlorine and potassium. Moving farther away from the inert gases in the rows of the periodic table gave elements that were generally less reactive and had higher valences. Abegg suggested that elements tended towards configurations with a "magic" electron configuration, for example potassium losing an electron to chlorine to form potassium chloride, both of which then had magic electron configurations. Valence, then, was equivalent to the deficit or excess of electrons relative to a magic number.
Abegg's concept had a logical flaw, however, in that he based it entirely on ionization: one element wanted to give up electrons, the other wanted to take them. That was difficult to argue against in the case of, say, table salt, NaCl, but it was much more arguable in the case of common diatomic molecules such as Cl2, since it would mean that a chlorine atom wanted to give up and take electrons simultaneously.
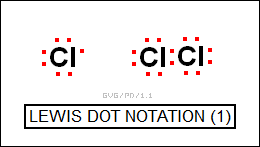
Lewis and Langmuir managed to get the idea to work by suggesting that atoms could also share electrons to obtain one of the magic number values. Argon had the pattern of magic numbers 2,8,8 and was stable; chlorine had one less electron, giving the pattern 2,8,7. With the pattern 2,8,8, chlorine would have a stable electron configuration; two chlorine atoms could achieve such a stable configuration by each "holding on" to one electron of the other, without the electron being given up. Lewis came up with a simple "dot notation" to make the idea easier to grasp, envisioning an atom as bracketed by from one to eight dots representing electrons, and then joining atoms together to get full complements of eight electrons:
Of course hydrogen was the exception to the dot rules, since it only had one electron, but that worked out, too:
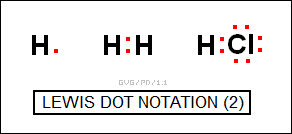
In modern terms, the complete transfer of a electron or electrons from one atom to another created an "ionic" bond, while the sharing of electrons between atoms created a "covalent" bond. The scheme was a triumph of scientific deduction, providing a highly useful model of chemical bonding even when the underlying physics was not understood at all at the time.
Originally, Lewis had conceived of his "octet rule" in terms of completing all the corners of a cube, which would then be enclosed in another cube, and so on. It was an interesting idea, with Lewis actually attempting to promote his "cubic atom" theory well into the 1920s, but the cube notion turned out to be just a gimmick. There was some tension between Lewis and Langmuir over their theory of chemical bonds: Lewis published his ideas in 1916, with Langmuir polishing them up a bit -- in particular, clarifying the concept of the covalent bond -- and publishing them in 1919. Langmuir was a better communicator than Lewis, and managed to sell the idea more successfully. However, the two stayed on friendly terms.
* Along with a workable if not very detailed model of chemical bonding, chemists also acquired the first satisfactory explanation of acids and bases. In 1923, a Danish chemist named Johannes Nicolaus Bronsted (1879:1947) suggested that an acid tended to lose a hydrogen ion to a solvent -- making it a "proton donor", and leaving it negatively charged -- while a base tended to acquire a hydrogen ion from a solvent -- making it a "proton acceptor", and leaving it positively charged . In the case of water, a donated proton is acquired by a water molecule, H2O, to become the "hydronium" ion, or H3O+. If a base accepts a proton from the water, the H2O molecule becomes a "hydroxyl" ion, or OH-.
BACK_TO_TOP* The Lewis-Langmuir model of chemical bonding was a remarkable insight for its time, but the development of quantum physics in the 1920s, in particular the invention of the Schroedinger equation, gave chemists a much more powerful tool for understanding chemical bonding.
Using the Schroedinger equation and other information obtained by the physicists, chemists were able to finally understand the architecture of the atom and the underlying basis of Mendeleev's periodic table. The sets of orbitals and the electron shells they defined established the bonding (and many other) properties of the elements. As the atomic number of the elements increased, the orbitals of electron shells were gradually filled up.
The outermost shell of an element was the major determinant of its bonding properties. The electrons in the outermost shell are called "valence" electrons. For hydrogen and helium, the outermost shell (actually the only shell) can accommodate two electrons. Hydrogen has one valence electron, and so two hydrogen atoms tend to bond together to share their electrons, forming the molecular hydrogen molecule, H2. Helium has two valence electrons, meaning its outermost shell is full, and so it won't bond with other atoms under anything resembling normal circumstances.
For other elements, as a general rule the outermost shell of elements can accommodate a maximum of eight electrons, a notion already established in an empirical form by Lewis's octet rule. Sodium has one valence electron, while carbon and silicon have four, nitrogen has five, oxygen six, and chlorine seven. That means that sodium and chlorine will bond together to form NaCl, -- sodium chloride or common table salt. Similarly, carbon will bond with four hydrogen atoms to form CH4, methane, or bond with two oxygen atoms to form CO2, carbon dioxide. Nitrogen will bond with three hydrogen atoms to form NH3, ammonia.
The organization of Mendeleev's periodic table reflects this structure, with elements in the same column having similar reactive properties: elements in the leftmost column, like fluorine and sodium, are very reactive, while those in the rightmost column, like helium, are all noble gases and hardly reactive at all.
One of the interesting properties of the electronic configuration of the elements is that as the atomic numbers of the elements increase and the electron orbitals fill up, the higher shell in the filling sequence is not necessarily the outermost shell. This is the case for the rare earth elements: they all have the same outermost shell, with electron orbitals being filled up in a shell underneath, which is why the rare earths have such similar properties and are so difficult to separate. The generally unstable actinides also have a "buried" shell and so have common chemical properties.
* In 1927, two German physicists, Walter Heitler (1904:1981) and Fritz London (1900:1954), used the equation to determine the bonding in a simple diatomic hydrogen molecule (H2). This was a big first step, and the American chemists John C. Slater (1900:1976) and Linus Pauling (1901:1994) went from there to construct a full quantum-mechanical theory of chemical bonding. Pauling would get the Nobel Prize in chemistry in 1954 for this work; incidentally, he was also the only person to win both a science prize and the peace prize, which he was awarded in 1962 for his nuclear disarmament activism.
In modern times, chemists have identified several classes of chemical bonds:
Incidentally, the tendency of atoms to tear an electron loose from another atom is called "electronegativity", with elements to the right in the periodic table being increasingly electronegative relative to those to the left. A molecule made up of an element with a low electronegativity, and an element with a high electronegativity -- that is, with the two elements in columns well apart in the periodic table -- will be ionic, with table salt (NaCl) being a good example. When the electronegativities of the atoms are unbalanced, the bonding tends to distort the charge distribution of the resulting molecule, making it "polarized", with a positive end and a negative end. Polarized molecules can form weak bonds between each other.
The bond will become increasingly covalent as the electronegativities of the two elements become more alike -- that is, if the elements are close together in the periodic table. Carbon dioxide, CO2, is a good example. Of course, atoms of the same element will form purely covalent bonds when they join together, with good examples being molecular hydrogen (H2), molecular oxygen (O2), and molecular chlorine (Cl2). Such molecules are not polarized.
* In practice, chemists use a range of models to describe chemical bonding. The Lewis octet rule is handy for simple analyses, but for more detailed work, quantum theory has to be used. Slater and Pauling's work on quantum chemistry involved two associated theories, the "valence shell electron pair repulsion (VSEPR)" theory and the "valence bond" theory. They are two sides of the same coin. VSEPR simply states that the valence electrons (or pairs of electrons, when two electrons with opposed spin share an orbital) repel each other and force the bonds to be as far away from each other as possible. VSEPR doesn't specify how many bonds there are, it just specifies the bond angles as a guideline to molecular configuration.
For example, the methane molecule, CH4, has four hydrogen atoms covalently bonded to a carbon atom. VSEPR dictates that the bond angles will be at the corners of a tetrahedron, and so methane is a tetrahedral-shaped molecule. Similarly, ammonia (NH3) has a tetrahedral structure, with the nitrogen atom at one corner. It might seem more logical from VSEPR theory that it would be a flat triangle, with the nitrogen atom at the center, but nitrogen has five valence electrons, meaning that one orbital is full with two electrons of opposed spin, and these two electrons provide a repulsion that forces the three hydrogen atoms down to the corners of the tetrahedron.
Valence bond theory complements VSEPR by specifying the number of bonds and the bonding arrangement, introducing a concept known as "hybridization" that involves a "mixing" or "summing" of orbitals to set up the observed bonding arrangement. Pauling also came up with the notion of "resonance". By the octet rule, an oxygen atom, which has a valence of six, can bond with two hydrogen atoms, each with a valence of one, to form the water (H2O) molecule. In a somewhat more devious way, two oxygen atoms can simultaneously steal two electrons from each other to form the diatomic oxygen (O2) molecule. It was this resonance that explained the stability of the benzene ring. However, the ozone (O3) molecule remains a bit of a puzzle.
* Sometimes simplified models won't do, demanding the use of the "molecular orbital" approach, developed by Friedrich Hund (1896:1997) and Robert S. Mulliken (1896:1996), which involves applying and solving the Schroedinger equation for an entire molecule instead of just one atom. Examples of when molecular orbital calculations might be required include computer simulations of the behavior of explosives and combustion of fuels in high-speed "scramjet" engines; design and evaluation of molecules for new drugs; and design of improved lubricants, plastics, and ultra-hard materials.
As mentioned, the Schroedinger equation can't be solved exactly for atoms with more than one electron. That in itself is not a roadblock, since there are approximate methods of solution that can give results to any desired level of precision; the problem is that obtaining such precision requires immense computing horsepower. The simplest mathematical model for ethanol, with nine atoms, requires 26 mathematical functions, and each electron and nucleus in the model interacts with every other electron and nucleus.
Even with modern supercomputers, molecular simulations based directly on the wave equation can be performed only on molecules up to a few hundred atoms in size. The response has been to devise smarter, simplified strategies for modeling large molecules, sometimes using measured data to replace calculations. Other computer simulations have been devised for well-ordered materials such as crystals, using simple models such as, say, imagining the structure as a set of balls linked by springs that represent the forces holding them in balance.
In addition, there is the secondary, but still non-trivial, matter of writing such complicated programs so that they work efficiently and reliably, and obtaining useful input and output of results. Graphics programs have been developed to allow display and manipulation of molecules, for example to examine how a particular drug molecule interacts with various biomolecules.
Ultimately, computational chemists hope to be able to precisely design molecules for a particular task from the specifications for that task, but the field is still in its infancy, and that sort of magic will take a great deal of work. One promising avenue of investigation has been machine-learning systems, which are "trained" by being given a huge set of real-world of molecules matched to their effects, with the system then able to provide candidate molecules after being given their desired effects.
BACK_TO_TOP