
* Codebreakers proved so successful in World War I that after the war, governments and military forces looked for new ways to ensure communications security. The answer seemed to lie in new "cipher machines" that provided ciphers of unprecedented complexity.
* After the First World War, the Germans discovered that their ciphers had been broken, and resolved to improve their cipher security. They chose to use machines to achieve that goal.
The idea of using machines to encipher and decipher messages was not new. The simple "cipher disk" goes back to the 15th Century, when it was invented by Leon Alberti, one of the fathers of the polyalphabetic substitution cipher. The cipher disk consists of two nested disks, including an outer disk labeled with all the letters of the alphabet, and an inner disk also labeled with all the letters of the alphabet -- but not necessarily in the same order. The outer disk defines the plaintext alphabet, while the inner disk defines a monoalphabetic substitution cipher alphabet.
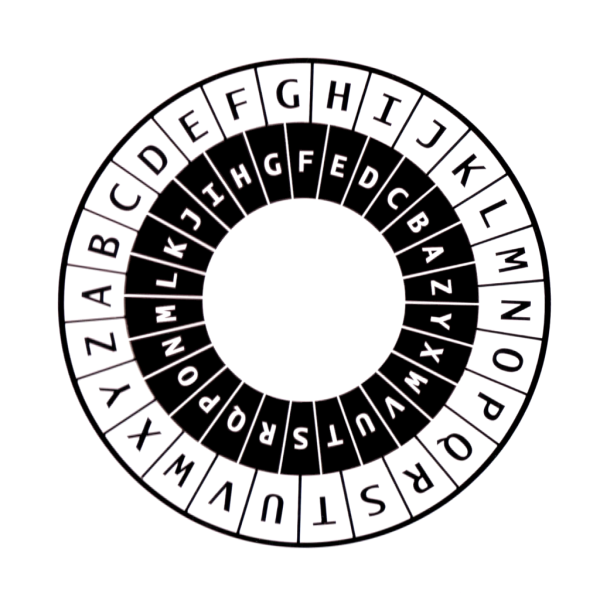
Suppose Alice takes her cipher disk and rotates the inner disk so that the letter "A" lines on the inner disk lines up with, say, the letter "q" on the outer disk. She can then encipher a message by taking each letter, looking up the plaintext letter on the outer disk, and then writing down the matching ciphertext letter next to it on the inner disk.
The cipher disk can be also made in the form of a "slide", with two alphabets written on strips of cardboard, or whatever, that can be slid next to each other. Of course, each slide should have two repeating alphabets to permit them to be read conveniently when offset.
* In these cases, the cipher remains a feeble monoalphabetic substitution cipher, which is not only easy to crack, but also so easy to use that the cipher disk hardly seems very handy. Where the cipher disk comes in useful is in dealing with a Vigenere cipher.
For example, suppose Alice wants to encrypt a message using a Vigenere cipher with the cipher key word "WARTHOG". To encipher the first letter, she moves the "W" on the inner disk to match up with the "a" on the outer disk, and then finds the ciphertext letter on the inner disk matching the desired plaintext letter on the outer disk.
Next, Alice enciphers the second letter on the inner wheel by moving the "A" on the inner disc to match the "a" on the outer disk, then looking up the ciphertext letter on the inner disk that matches the desired plaintext letter on the outer disk. She repeats this process for "R", "T", "H", "O", and "G", and then starts all over again at "W", repeating the cycle through the key until the message has been completely enciphered. The cipher disk reduces the labor of using a Vigenere cipher, and remained in use for centuries. It does introduce the minor weakness of using the same substitution cipher for each letter of the alphabet, but multiple cipher alphabets weren't always used with Vigenere ciphers anyway.
One of the most famous examples of the cipher disk is the "Captain Midnight Code-o-Graph", which was associated with the Captain Midnight radio program of the 1930s and 1940s. Captain Midnight fans could write in to Ovaltine, one of the program's sponsors, to get the Code-o-Graph, and then decode secret messages that Captain Midnight would occasionally announce at the end of the program. Except for the fact that the Code-o-Graph used numbers instead of letters for the cipher alphabet, it was just a classic cipher disk.
BACK_TO_TOP* Another simple cipher machine was invented by American President Thomas Jefferson in the 18th century, but did not come into wide use until it was reinvented by Commandant Etienne Bazeries, the conqueror of the Great Cipher, a century later. It is now known as the "Bazeries cylinder".
A Bazeries cylinder consists of a set of roughly 20 to 30 numbered disks, with a different cipher alphabet on the edge of each disk, and a hole in the center of the disks to allow them to be stacked on an axle. The disks are removeable and can be mounted on the axle in any order desired. The order of the disks can be considered the cipher key for the Bazeries cylinder, with both Alice and Bob arranging the disks in the same predefined order.

To encrypt a message, Alice rotates the disks to produce the plaintext message along one "row" of the stack of disks, and then selects another row as the ciphertext. To decrypt the message, Bob rotates the disks on his cylinder to produce the ciphertext along a row. It is handy if both Alice and Bob know the offset of the row, but not really necessary since Bob can simply look around the cylinder to find a row that makes sense.
For example, a simplified "toy" Bazeries cylinder, using only ten disks, might be organized as shown below, with each disk "unwrapped" into a line and each marked with a designating number:
: 1: < ZWAXJGDLUBVIQHKYPNTCRMOSFE < : 2: < KPBELNACZDTRXMJQOYHGVSFUWI < : 3: < BDMAIZVRNSJUWFHTEQGYXPLOCK < : 4: < RPLNDVHGFCUKTEBSXQYIZMJWAO < : 5: < IHFRLABEUOTSGJVDKCPMNZQWXY < : 6: < AMKGHIWPNYCJBFZDRUSLOQXVET < : 7: < GWTHSPYBXIZULVKMRAFDCEONJQ < : 8: < NOZUTWDCVRJLXKISEFAPMYGHBQ < : 9: < XPLTDSRFHENYVUBMCQWAOIKZGJ < : 10: < UDNAJFBOWTGVRSCZQKELMXYIHP <
Suppose that the "key", the sequence of disks, for the Bazeries cylinder is:
7:9:5:10:1:6:3:8:2:4
-- and Alice wants to send the message "retreat now" to Bob. Then she rearranges the disks as per the key and rotates each disk to obtain the plaintext, which is shown at the left, with spacing added to highlight it:
: 7: < R AFDCE O NJQGWTHSPYBXIZULVKM < : 9: < E NYVUB M CQWAOIKZGJXPLTDSRFH < : 5: < T SGJVD K CPMNZQWXYIHFRLABEUO < : 10: < R SCZQK E LMXYIHPUDNAJFBOWTGV < : 1: < E ZWAXJ G DLUBVIQHKYPNTCRMOSF < : 6: < A MKGHI W PNYCJBFZDRUSLOQXVET < : 3: < T EQGYX P LOCKBDMAIZVRNSJUWFH < : 8: < N OZUTW D CVRJLXKISEFAPMYGHBQ < : 2: < O YHGVS F UWIKPBELNACZDTRXMJQ < : 4: < W AORPL N DVHGFCUKTEBSXQYIZMJ <
She then selects the ciphertext from the sixth row of the cylinder up from the plaintext. This ciphertext is also highlighted above with spacing, and gives:
: OMKEGWPDFN
When Bob gets the ciphertext, he rearranges the disks on his cylinder to the key arrangement; rotates the disks to give the ciphertext; and reads the plaintext six rows down from the ciphertext, or simply looks over the cylinder for a row that makes sense.
* The Bazeries cylinder was the basis for the US "M-94" cipher machine, which was introduced in 1922 and derived from work by Parker Hitt. In 1914, Hitt had experimented with the Bazeries device, building one prototype using slides on a wooden frame, with the cipher alphabets printed twice consecutively on the slides, and then another using disks of wood. He forwarded his experiments up the Signal Corps chain of command, and in 1917 Joseph Mauborgne refined the scheme, with the final result being the M-94.
The M-94 used 25 aluminum disks on a spindle. It was used by the Army, Coast Guard, and the Radio Intelligence Division of the Federal Communications Commission until early in World War II. The Army reverted to Hitt's original slide scheme with the "M-138-A" cipher machine, which was introduced in the 1930s and was used by the US Navy and US State Department through World War II. The M-138-A featured 100 strips, with 30 selected for use in any one cipher session. It was a great improvement in security for the State Department, which during the interwar years had used laughably insecure codes, even in one case a standard commercial telegraph code.

* The Bazeries cylinder is strong, and Bazeries, a competent but opinionated man, regarded it as unbreakable. In fact, it is hardly impregnable, and the "Pers z" code-breaking group of the German Foreign Office cracked the M-138-A in 1944. However, by that time the Americans had much more sophisticated cipher systems in operation, and it was too late for the Germans anyway. Many of the decrypts of Allied communications presented to the German high command were disregarded, because all they did was confirm bad news that nobody wanted to acknowledge in an environment where defeatism could be punished by death.
One major weakness of the Bazeries cylinder is that the offset from the plaintext letter to the ciphertext letter for the cipher alphabet on each disk will be exactly the same. In the example shown above, this offset is six letters.
Suppose Holmes has captured the simplified Bazeries cylinder described in the example above, with ten disks. This should not be enough to permit him to decipher messages with it, since he also has to know the key, or the arrangement of the disks on the cylinder. Even for this simplified Bazeries cylinder, the number of possible permutations of the disks are:
: 10! = 3,628,800
-- which makes trial and error testing of the arrangement of the disks completely impractical to perform by hand, though a modern computer wouldn't have any problem with such a search.
Now further suppose that Holmes has a crib. For example, suppose he knows that the first block of plaintext enciphered by the simplified Bazeries cylinder is the string:
: heilhitler
This is exactly ten letters long (what a coincidence!) and can be enciphered in a single pass with the simplified Bazeries cylinder. The corresponding ciphertext is:
: AZNCZEAPBH
The remainder of the message is of course a complete mystery for the moment. Fortunately, Holmes can use this crib to allow him to decipher all the following blocks of the message.
Holmes has no idea of which disk is used to encipher which letter, but he does know that the offset between the plaintext letter and the ciphertext letter must be the same for all ten characters. This gives him a way of penetrating the cipher by lining up the plaintext and ciphertext characters of the crib; forming them into pairs; determining the offsets for the plaintext letters and ciphertext letters for each disk; and then searching for a common offset in the matrix of offset.
Holmes knows that the correspondence between the two sets of letters is as follows:
: h:A : e:Z : i:N : l:C : h:Z : i:E : t:A : l:P : e:B : r:H
With this in mind, Holmes takes disk 1, which has the cipher alphabet:
: 1: < ZWAXJGDLUBVIQHKYPNTCRMOSFE <
The first letter pair is "h:A", and Holmes counts along the disk to determine that the offset between the two letters is 15. The second letter pair is "e:Z", and he sees right away that the offset is 1. He continues this process for each letter pair for disk 1, and then goes through the same procedure for the nine other disks, producing the following table:
: h:A e:Z i:N l:C h:Z i:E t:A l:P e:B r:H : ------------------------------------------------ : 1: 15 1 6 12 13 14 10 9 10 19 : 2: 14 5 6 3 16 4 22 23 25 7 : 3: 15 15 4 2 17 12 14 25 10 7 : 4: 18 7 10 7 14 20 12 25 1 6 : 5: 4 14 20 13 20 7 21 14 25 24 : 6: 22 16 3 17 10 19 1 14 14 14 : 7: 14 15 14 8 7 12 15 19 12 13 : 8: 21 12 12 22 5 2 14 8 8 14 : 9: 11 14 15 14 15 14 16 25 5 2 : 10: 5 23 5 21 17 21 20 6 14 12
As Holmes prepares the table, the value "14" quickly jumps out at him as a common element, and in completion of the table proves to be the only common element. This is obviously the row offset from the plaintext to the ciphertext. He strips the other values out for clarity:
: h:A e:Z i:N l:C h:Z i:E t:A l:P e:B r:H : ------------------------------------------------ : 1: - - - - - 14 - - - - : 2: 14 - - - - - - - - - : 3: - - - - - - 14 - - - : 4: - - - - 14 - - - - - : 5: - 14 - - - - - 14 - - : 6: - - - - - - - 14 14 14 : 7: 14 - 14 - - - - - - - : 8: - - - - - - 14 - - 14 : 9: - 14 - 14 - 14 - - - - : 10: - - - - - - - - 14 -
Finally, Holmes rearranges the disks in the table to reflect the correct order of the letters on the cylinder:
: h:A e:Z i:N l:C h:Z i:E t:A l:P e:B r:H : ------------------------------------------------ : 2: 14 - - - - - - - - - : 5: - 14 - - - - - 14 - - : 7: 14 - 14 - - - - - - - : 9: - 14 - 14 - 14 - - - - : 4: - - - - 14 - - - - - : 1: - - - - - 14 - - - - : 3: - - - - - - 14 - - - : 6: - - - - - - - 14 14 14 : 10: - - - - - - - - 14 - : 8: - - - - - - 14 - - 14
This gives the key:
: 2:5:7:9:4:1:3:6:10:8
In this case, there are no ambiguities in the arrangement of the disks, but if there had been, a little testing of subsequent blocks of the ciphertext would reveal the proper order.
* In the real world, a Bazeries cylinder has 20 or 30 disks, not ten, and it is unlikely that there would be a single crib that would span the entire cylinder. The approach described above still works. Even if the cylinder had 30 disks and a crib only had five letters, Holmes could build up a table of the offsets for each of the 30 disks for the five letter pairs, and use it to greatly narrow down the possibilities for the offset and the disks used for the crib.
Holmes could repeat the procedure with several independent cribs in the same message, almost certainly pinning down the offset quickly and giving an improved knowledge of the order of the disks. Once the offset has been determined, then Holmes would have what amounted to a straight transposition of the letters not determined by tinkering with the cribs, and use methods such as multiple anagramming to crack it.
BACK_TO_TOP* By the end of the First World War, cryptologists were working on much more ambitious electromechanical cipher machines that were far more sophisticated than the Bazeries cylinder, and indeed seemed to be all but impregnable. The most famous of these cipher machines was the "Enigma" machine, initially patented in 1918 by a German engineer named Arthur Scherbius.
Scherbius was a member of the partnership of Scherbius & Ritter, an engineering firm that worked on any technologies that seemed like they might make some money. The company had been formed in 1918, with Scherbius acting as the company's technical guru, while his friend Ritter handled the business side.
Scherbius's Enigma was based on an electromechanical equivalent of the cipher disk, called the "rotor". To understand how a rotor-based cipher machine works, let's imagine a series of cipher machines, starting out with one that's stupidly simple and working our way up.
* The stupidly simple cipher machine, which we'll call the "Mark 1", looks like a box with a typewriter keyboard; a bank of lights, with each light labeled with a letter of the alphabet; and wires running from each key to the corresponding light. Press the "a" key, and the "A" light blinks on, press the "b" key, and the "B" light blinks on, and so on.
Rearranging the wiring from keys to lights according to the mappings of a monoalphabetic substitution cipher, "scrambling" the connections, would allow the box to be used to encipher a message. Alice could type in her plaintext message, and write down the letters that lit up to produce her ciphertext. Of course, Bob would need a second box with a reversed wiring scheme to convert ciphertext back to plaintext, but we'll ignore that consideration for now, since we'll ultimately see there is a way around the need for separate boxes to encipher and decipher a message.
* While the Mark 1 would be a workable tool, it would also be a clumsy one, less useful than a cipher disk and far more expensive and unreliable. Let's consider a modification of the box to build an improved cipher machine, the "Mark 2".
Suppose we build a disk with 26 electrical contacts on each side, and redesign the box so that we can slip this disk into a slot in the middle. The direct connections between the keyboard and the lights in the box are cut. The keyboard is wired to a set of 26 electrical contacts to connect to one side of the disk, while the lights are wired to 26 electrical contacts to connect to the other side of the disk.
The contacts on the two sides of the disk itself are linked by an internal wiring pattern that scrambles the connections, implementing a monoalphabetic substitution cipher. The disk is the rotor. The idea is generally credited to American cryptographer Edward Hebern, though it was basically invented independently in a number of different places at almost the same time.

Using a rotor instead of a permanently wired connection pattern makes the box more useful. Now Alice can change the box's connection pattern by just changing the rotor. Not only that, but if we label the edge of the rotor with the letters "A" through "Z", Alice can turn the rotor to 26 different identifiable positions, allowing the box to encipher and decipher all 26 shift ciphers of the basic monoalphabetic substitution cipher implemented by the rotor.
Alice could then implement a Vigenere cipher using the Mark 2 by turning the rotor to different letters every time she presses a key. For example, if she uses the "WARTHOG" cipher key word, she could rotate the wheel to show the letter "W", then press a key and get the cipher letter; move it to show the letter "A" and get the cipher letter; move it to "R" and get the cipher letter; and so on.
* However, all this measure has done is bring the box up to the same level of capability as a cipher disk. We can come up with a "Mark 3" that does better, using an automatic approach, with the rotor automatically turning every time a key is pressed, returning to the original position after 26 keypresses and then starting all over again.
This is much more convenient than manually setting the rotor to the letters of a key, and it preserves the Vigenere cipher's ability to confound frequency analysis. The drawback is that the cipher is also much more predictable, since the sequence of different substitution alphabets is fixed, though Alice can change the starting point of the sequence by setting the rotor to one of its 26 possible initial positions.
* Given a rotor that increments every time a key is pressed, we now have a workable, if not very secure, cipher machine. However, let's go to a "Mark 4" cipher machine that will be much harder to crack. Let's suppose we redesign the box to use two rotors with different wiring patterns, so that the connections are routed from the keyboard to the lights through both rotors.
The first rotor turns one position every time Alice presses a key, as before, but the second rotor remains stationary, only advancing a position when the first rotor completes a full revolution, after 26 keypresses. This means that, instead of having a sequence of 26 different substitution alphabets, we now have a sequence of 26 * 26 = 676 different substitution alphabets.
We can then devise a "Mark 5" cipher machine that builds on this scheme by adding a third rotor in series with the first two, designed so that it only turns one position every time the second rotor completes a full revolution, or once every 676 keypresses. The scheme is very similar to that which causes the different digits of an old mechanical car odometer to increment by ones, tens, hundreds, and so on.
Now we have a sequence of 26 * 26 * 26 = 17,576 different substitution alphabets. The sequence may be deterministic, but given the equivalent number of 17,576 starting positions for the rotors, cracking a message enciphered by this machine would be tedious, even if Holmes had a copy of an identical machine and tried all the rotor positions. Incidentally, such an assembly of multiple rotors is referred to as a "basket".
The three rotors are still removeable, and so Alice can swap their positions in six different ways:
: 123 : 132 : 213 : 231 : 312 : 321
This multiplies the number of sequences by six, for a total of 6 * 17,576 = 105,456 possibilities. Any trial and error approach to cracking a ciphertext encrypted by this machine, even given an identical machine, becomes that much more difficult. Not only that, but the number of different substitution alphabets is large, and makes the Kasiski approach to frequency analysis of a Vigenere cipher difficult to use at best.
* The imaginary Mark 5 cipher machine is almost an Enigma, but the actual Enigma machine incorporated three refinements. The first refinement involved two features that seem baffling unless they are considered together with their implications, sort of like an extremely elaborate joke that seems to make no sense until the punchline is delivered:
With this arrangement, pressing a key formed a connection all the way through the rotors, around through the reflector, and then back through the rotors again to light up a lamp. This has the implications:
The "punchline" of this entire scheme is that the Enigma machine can both encipher and decipher messages. Its operation is "reciprocal", in that if "a" is enciphered as "Z", then "z" is enciphered as "A". If this were not so, two different machines, with the connections to the keyboard and bank of lights swapped, would be needed to decipher the message. The use of the reflector permits only one Enigma machine to be used for both tasks.
The beauty of this scheme is that no particular care has to be taken in wiring the rotors or the reflector to ensure reciprocity. Reciprocal operation is just the consequence of the fact that connections from key to light are bidirectional. Reciprocity does lead to some small weaknesses in the cipher output of the Enigma machine, the first being that no letter will ever be enciphered as itself; the second being that if Holmes knows that, say, "e" is enciphered as "Q", then he also knows that "q" is enciphered as "E".
* The second refinement was the plugboard or "Stecker". Essentially, the connections between the keyboard / light bank pairs and the front of the first rotor, were connected by a set of jumper cables that could be moved around by the Enigma operator. Moving a cable allowed swapping a pair of letters, for example a cable could be moved to swap the letters "g" and "t".
The Enigma operator could swap six pairs of letters. This may not seem like much of a feature, but in principle it greatly complicated the lives of codebreakers. Let's suppose we select 12 letters from the 26 available to swap as pairs. The number of possible ways to select 12 items from 26 is:
: 26*25*24*...*15 = 26!/(26-12)! = 26!/14!
That is, there are 26 possibilities for the first item, then 25 possibilities for the second item, then 24 for the third, and so on, until 12 items have been selected. However, this assumes that the order in which the items are selected is important, and in this case it is not. Given 12 items, the number of different possible ways to arrange their order is:
: 12*11*10*...*1 =12!
-- and so the possible different number of sets of 12 items selected from 26, disregarding their order, is:
: 26!/(14!*12!)
The 12 letters having been selected, we can select 6 letters from the set of 12 and match them to the remaining 6 letters to form up the pairs of letters to be swapped. The number of possible ways to select 6 items from 12 is:
: 12*11*10*9*8*7 = 12!/6!
Given a set of 6 selected letters, the remaining 6 letters can be matched up in 6! different ways, which would seem to multiply the total number of pairs by 6!. However, the order of all the possible sets of 6 pairs of letters isn't important; there are 6! possible orderings of the same 6 pairs of letters, so the number of possible letter pairs is still 12!/6!.
There remains a catch in that for every set of 6 pairs there is a mirror and equivalent set of 6 pairs -- A mapped to Z versus Z mapped to A and so on -- and that means the total must be divided by 2 to eliminate the redundant sets. That gives a total number of distinct sets of 6 letter pairs as:
: 12!/(6!*2) = 332,640
Multiplying the total number of possible sets of 12 items that can be selected from 26 items, times the total number of 6 pairs that can be selected from 12 items, ignoring order in all cases, gives:
: 26! 12! : ------- * ---- = 26!/(14!*6!*2) = 3.21E12 : 14!*12! 6!*2
This was the total number of ways that six letters could be swapped using the Stecker. To be sure, all the Stecker did was define a monoalphabetic substitution cipher, which in itself could be easily cracked using frequency analysis. However, the Stecker was a front end to the rotor system, which defied frequency analysis, and so it seemed that the confounding effects of the Stecker made the Enigma machine's output extremely difficult to crack.
* There was a third refinement in the Enigma machine, called the "ring", which added yet another level of complications. It was a ring around the edge of each rotor that had a notch in it and could be repositioned to any of the 26 positions in the rotor. This notch was what caused the next rotor in the basket to advance. To show the effect of moving the ring, imagine that we have "toy" rotors only have three positions each. In the default ring positions, this would give a sequence of 27 rotor positions as follows: between every full rotation of the first rotor for clarity:
: 1 1 1 : 2 1 1 : 3 1 1 : 1 2 1 : 2 2 1 : 3 2 1 : 1 3 1 : 2 3 1 : 3 3 1 : 1 1 2 : 2 1 2 : 3 1 2 : ... : 1 3 3 : 2 3 3 : 3 3 3 : 1 1 1 : ...
Suppose the ring on the first rotor was moved so that the second rotor would advance on the transition from 1 to 2 instead of from 3 to 1. That would modify the sequence as follows:
: 1 1 1 : 2 2 1 : 3 2 1 : 1 2 1 : 2 3 1 : 3 3 1 : 1 3 1 : 2 1 2 : 3 1 2 : 1 1 2 : 2 2 2 : 3 2 2 : ... : 1 3 3 : 2 1 1 : 3 1 1 : 1 1 1 : ...
Now suppose the ring on the second rotor was then changed so the third rotor would advance on the transition from 2 to 3 instead of 1 to 2. That would give another sequence:
: 1 1 1 : 2 2 1 : 3 2 1 : 1 2 1 : 2 3 2 : 3 3 2 : 1 3 2 : 2 1 2 : 3 1 2 : 1 1 2 : 2 2 2 : 3 2 2 : ... : 1 3 1 : 2 1 1 : 3 1 1 : 1 1 1 : ...
Since the rings can be set into one of three positions on each rotor, that means that there are a total of 3 * 3 = 9 possible sequences. Of course, the nock on the final rotor doesn't do anything, since it's the last rotor in the basket. Since the rotors of the Enigma actually had 26 positions, and so the rings added another factor of 26 * 26 = 676 possible variations in the Enigma sequence.
* The setup of the Enigma machine was very important. The setup involved specifying the plugboard connections, the order of the rotors, the initial positions of the rotors, and the ring positions. This setup was the cipher key for the Enigma machine.
The Enigma machine evolved through a series of versions, but in its full production form it was a wooden box about the size of a boot box. The wooden lid was lifted to reveal the keyboard, the lights, and the rotors. The rotors were concealed behind little windows that only showed one letter on the edge of each rotor, once again in a way resembling a car's odometer. There were thumbwheels next to each rotor to allow it to be turned by the operator. Another panel could be lifted to allow access to the rotors, so they could be removed and reinserted in different orders. The front of the box hinged down to reveal the plugboard.

In practice, Enigma operators were given a codebook of setups that would change, say, each day, and the operators would all perform the same setup using the same "daykey" at the same time. After performing the proper setup, the Enigma operator would take a plaintext message, type it in on the keyboard, and then write down the letters that appeared on the lights. Since the Enigma machine only had letters, no numbers or punctuation, numbers were spelled out, for example ONE SEVEN SIX POINT FIVE NINE, as was punctuation, for example COMMA, QUOTE, or STOP.
The enciphered message was then sent in Morse code. The Enigma operator on the receiving end then punched in the ciphertext on the Enigma's keyboard, and wrote down the plaintext as it appeared on the lights.
* As far as Scherbius could see, his Enigma machine was impregnable. Frequency analysis couldn't touch it, and a brute-force approach was completely ruled out. Even if a codebreaker had access to an Enigma machine, the number of possibilities for the daykey was very large. Given that the three rotors could be inserted in different orders, the rotors could be rotated to different positions, the plugboard could swap six pairs of letters, and the two rings could be set in 676 different ways, the number of possible setups was:
: 6*(26^3)*(3.21E12)*676 = 2,29E20
This is formidable even by modern standards. Even assuming that a computer could test for a million different daykeys in a second, it would still take over 7 million years to check them all.
Scherbius hoped to sell Enigma machines to businessmen to protect them from industrial espionage, but there were few takers. However, in 1923, Winston Churchill published THE WORLD CRISIS, his memoirs of the First World War, and the British Royal Navy also published their own history of the Great War. Both documents revealed that German ciphers had been cracked through much of the conflict. The German military had no previous hint of their failure and was thoroughly shocked. They decided to standardize on the Enigma machine to ensure security in the future, and in 1925 Scherbius & Ritter began to ramp up production of Enigma machines to meet demand. The German military eventually bought more than 30,000 Enigma machines.
The success of the Enigma machine must have been satisfying to Arthur Scherbius. He was killed in an accident in 1929, and he never knew that his "impregnable" Enigma machine would prove nothing of the sort.
BACK_TO_TOP* A wide range of cipher machines was built in the period between the World Wars, and some of them besides the Enigma are described in a later chapter. There was also a parallel effort to develop schemes to permit secure telephone conversations, using various electronic "scrambler" technologies.
Devices to provide telephone security date were developed only a few years after Alexander Graham Bell's telephone patent of 1876, but they did not come into use until the late 1920s. These scramblers operated by a number of principles. One was the manipulation of the "sub-bands" of speech on a telephone. A voice audio signal is a very complicated and unpredictable waveform, but it can be broken down into a set or "spectrum" of different simple "component" waveforms with a range of frequencies, with the spectrum changing over time.
The highest frequencies in normal human voice conversations range to over 7,000 hertz (Hz), but most of the higher frequencies don't make much difference, and so telephones only transmit in the "frequency band" between 300 Hz and 3,300 Hz. As anyone who uses a phone knows, this is perfectly adequate for speech communications, though it's certainly not high-fidelity sound. It is possible to sift out different sub-bands from the voice signal using electronic filters. For example, we could build a set of five filters to tear apart the spectrum of the voice signal as follows:
: filter 1: 300 to 900 Hz : filter 2: 900 to 1,500 Hz : filter 3: 1,500 to 2,100 Hz : filter 4: 2,100 to 2,700 Hz : filter 5: 2,700 to 3,300 Hz
These five sub-band signals could then be "modulated", or shifted in frequency, in various ways and mixed back together again to generate sounds that are hopefully incomprehensible to any eavesdropper. A parallel set of sub-band filters in the decoder would then sort out the scrambled speech and reassemble it correctly.
One simple sub-band scrambling scheme simply "inverted" the sub-bands, converting the output of filter 1 to the 2,700 to 3,300 Hz range, converting the output of filter 5 to the 300 to 900 Hz range, and so on. Another simple approach was to shift the output of filters 1 through 4 up a sub-band, and convert the output of filter 5 to the 300 to 900 Hz range.
These simple schemes were fairly predictable and really only protected a telephone conversation against someone who didn't have a descrambler. Worse, in some cases a word might leak through the scrambler system and remain perfectly intelligible even if an eavesdropper didn't have a descrambler. A more sophisticated scheme shuffled the sub-bands in a more or less random pattern that changed every few seconds or fractions of a second.
Another scheme was to split up a voice signal into time intervals and shuffle them around, sort of like an audio equivalent of a transposition. This would seem difficult to do in the days before digital electronics, but it was done with a clever modification of a magnetic tape recorder. The recorder played tape in a continuous loop that recorded a speaker's words. Just downstream from the record head was a set of, say, five read heads. Scrambler electronics could select one of the read heads in any order, allowing the order of voice samples to be rearranged. Of course, the decoder would need a similar set of record heads that were selected in the same order.
Such "time division" scrambling could be combined with sub-band scrambling for more security. Other schemes were to use systems that added noise to the speech signal, with the decoder subtracting the same noise; or varying the volume of the speech signal at a high rate, and of course with the decoder performing exactly the reverse changes in volume.
* Although telephone scramblers were used by both sides in World War II, they were known not to be very secure in general, and both sides often cracked the scrambled conversations of the other. Inspection of the audio spectrum using a spectrum analyzer often provided significant clues to the scrambling pattern. The insecurity of most telephone scrambler schemes led the US Army to obtain a truly secure scrambler, based on the one-time pad principle, known as "SIGSALY".
The name SIGSALY was not an acronym, instead being a cover name that sounded like an acronym. A prototype was developed by Bell Telephone Laboratories, better known as "Bell Labs", and demonstrated to the US Army. The prototype was called the "Green Hornet" after the popular radio show, because it made a hornet-like buzzing if somebody tried to eavesdrop on the conversation. The Army was impressed and awarded Bell Labs a contract for two systems in 1942. SIGSALY went into service in 1943 and remained in service into 1946.
SIGSALY used a random noise mask to encrypt voice conversations. The voice conversation was sampled for its amplitude once every 20 milliseconds, with the amplitude converted into one of six amplitude levels, with values from 0 through 5. The amplitude levels were on a nonlinear scale, with the steps between levels wide at low amplitudes and narrower at high amplitudes. This scheme, known as "companding" for "compressing-expanding", exploits the fact that the fidelity of voice signals is more sensitive to high amplitudes than to low amplitudes.

A random value from the same set of six levels was subtracted from each sampled voice amplitude value to encrypt them before transmission. The subtraction was performed in a "modulo" or "wraparound" fashion, meaning that if there was a negative result, it was added to six to give a positive result. For example, if the voice amplitude value was 3 and the random value was 5, then the subtraction would work as follows:
: 3 - 5 gives -2 : 3 - 5 gives -2 + 6 : 3 - 5 gives 4
-- giving a value of 4. In any case, the sampled value was then transmitted, with each sample level transmitted on one of six corresponding frequencies in a frequency band, a scheme known as "frequency-shift keying (FSK)". The receiving SIGSALY read the frequency values, converted them into samples, added the random values back to them to decrypt them, and converted them into a voice waveform. The addition was also performed in a "modulo" fashion, with six subtracted from any value over five. To match the example above, if the receiving SIGSALY got a sample value of 4 with a matching random value of 5, then the addition would be as follows:
: 4 + 5 gives 9 : 4 + 5 gives 9 - 6 : 4 + 5 gives 3
-- which gives the correct value of 3. If the concept of modulo arithmetic seems troublesome, it can be ignored for now. It's a simple idea and is explained in much more detail later.
The noise values were originally produced by large mercury-vapor rectifying vacuum tubes and stored on a phonograph record. The record was then duplicated, with the records being distributed to SIGSALY systems on both ends of a conversation. The records were effectively the SIGSALY "one-time pad", and of course were strictly controlled.
The records were played on turntables, but since the timing between the two SIGSALY terminals had to be precise, the turntables were by no means just ordinary record players. The rotation rate of the turntables was carefully controlled, and the records were started at highly specific times, based on precision time-of-day clock standards. Since each record only provided 12 minutes of key, each SIGSALY had two turntables, with a second record "queued up" while the first was "playing".
A dozen SIGSALY terminal installations were eventually set up all over the world. One was installed in a ship and followed General Douglas MacArthur during his South Pacific campaigns. It supported about 3,000 high-level telephone conferences. From a modern perspective, the whole scheme seems like a combination of the brilliant and primitive, but it worked very effectively -- though of course SIGSALY was too big and cumbersome for general use, and was only used for voice communications by the most important officials.
BACK_TO_TOP