
* Planck's explanation of black-body radiation, Einstein's explanation of the photoelectric effect, and Rutherford's discovery of the nuclear atom did not seem like threats to the logical underpinnings of the physics of the time, though they did cause considerable puzzlement. That puzzlement would result in a new model of the atom, constructed by the Danish physicist Niels Bohr, that would challenge traditional ideas -- and serve as a stepping-stone, through the work of other physicists such as Erwin Schroedinger and Wolfgang Pauli, to a completely radical view of nature at the submicroscopic "quantum" level.
* The problem with the atomic model proposed by Ernest Rutherford was that, as it stood, it was completely ridiculous. The positively-charged nucleus attracted the electrons in orbit around it; an electron being accelerated, as it would be when it was being pulled around the nucleus, would lose energy by emitting EM radiation and promptly spiral into the nucleus. That was the main reason why Nagaoka's speculations on the matter hadn't gone anywhere, and Rutherford himself didn't take the idea too seriously: his observations simply showed that it was the way things seemed to be, and as far as he was concerned, the theoreticians could figure out how.
In 1911, a young Danish physicist named Niels Bohr (1885:1962) came to Britain from Copenhagen to work in J.J. Thomson's lab. Thomson was not an easy person to work for, being a rumpled and abstracted sort who had a tendency to simply turn around and walk off while people were talking to him. Bohr's poor English did not improve communications, and when Bohr found an opportunity to sign up with Ernest Rutherford, Bohr did so without much hesitation, or for that matter much interference from Thomson. Rutherford was much easier to work for than Thomson, and when Bohr asked if he could work at home on theoretical studies, Rutherford agreed. It would prove to be a wise judgement on Rutherford's part.
Bohr was a plodding, single-minded person who could focus on difficult problems in an unhurried way for a long period of time. He was inclined to talk his ideas out non-stop against anyone who wanted to act as a sounding-board, coming up with a stream of concepts, probing them, discarding some and moving further on others, groping for and gradually converging on a solution. It was not a style that went over well with the direct and impatient. He gave considerable thought to the Rutherford atom in his studies, and continued his theoretical work after his return to Copenhagen in 1912. In a series of papers published from 1913 into 1915, Bohr came up with a way of saving the Rutherford atom.
Bohr proposed that electrons orbiting the nucleus of an atom could not occupy just any orbit, they could only occupy certain specific orbits, which he called "stationary states". A photon could make an electron jump from one state to a higher energy state, and it might emit a photon in a high state to then fall back to a lower state. While it was in a state, it wouldn't emit any EM radiation. Bohr further proposed that these stationary states were equivalent to orbits in which the orbital angular momentum of the electron was an integer multiple of Planck's constant -- or in other words, the angular momentum of the electron was quantized. For the normal one-electron hydrogen atom, this assumption gave the electron energies as:
electron_energy = -13.6 eV / n^2
-- where "eV" stands for "electron-volt" -- a measure of energy corresponding to the energy of an electron after accelerating through an electric field with a potential of one volt, equivalent to 1.602E-26 joule -- and "n" is an integer. What made this interesting was that it neatly explained the line spectra of the hydrogen atom. Einstein had shown that photon energy was given by:
photon_energy = Planck's_constant * frequency
A photon was emitted by the Bohr atom when an electron dropped from one state to a lower state. Such a change would become known as a "quantum jump", incidentally, and featured the interesting property that the electron would jump from one state to another in a discontinuous fashion, simply snapping from one state to the next without any delay between the two states. In any case, the energy of the photon emitted would be that of the difference in energies of the two states:
Planck's_constant * frequency = E1 - E2
Performing the calculations gave a very close description of the line spectra of the hydrogen atom. It also explained the Ritz combination principle. If a photon of one frequency was emitted by the quantum jump E1 - E2 and a photon of another frequency was emitted by the quantum jump E2 - E3, then a quantum jump of E1 - E3 would emit a photon with the sum of those two frequencies.
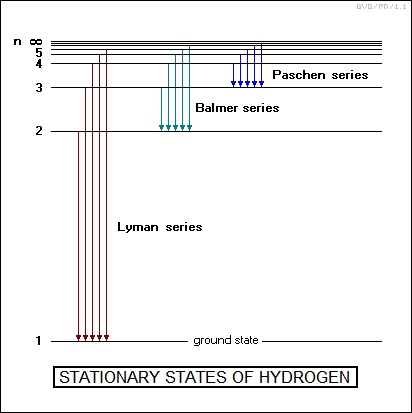
Bohr's initial concept gave a good accounting for the spectral lines of hydrogen, but it failed to account for what was known as the "fine structure" of the spectrum. Under close investigation, it turned out that most of the spectral lines separated into multiple, narrowly-spaced lines. Bohr's model initially assumed that the orbits of the electrons were circular, but in 1916, the German physicist Arnold Johannes Sommerfeld (1868:1951) proposed that the orbits might also be elliptical to varying degrees, with the various subordinate spectral lines corresponding to specific variations in the orbital configuration. Of course, in keeping with the spirit of the exercise, Sommerfeld showed that the variation in the orbits was quantized as well, given by an integer quantum value. If Bohr's quantum number n, the "principal quantum number", had a value of 1, the only value that Sommerfeld's "orbital quantum number" or "m" could have would be 0. If n had a value of 2, m could be 0 or 1. If n had a value of 3, m could be 0 or 1 or 2 ... and so on.
That still didn't do the job, since hydrogen atoms in magnetic fields demonstrated further complications in their spectral emissions, a phenomenon known as "Zeeman splitting" after the Dutch physicist Pieter Zeeman (1865:1943), who discovered it in 1896. Sommerfeld assumed that his orbitals were all in the same plane, but of course a hydrogen atom is a three-dimensional object and constraining the orbits to a single plane was clearly too restrictive. It became obvious that the orbitals could have different orientations, which were again quantized, taking on integer values. If Sommerfeld's orbital quantum number m had a value of 0, the "magnetic quantum number" or "ml" could only have a value of 0; if m had a value of 1, then ml could have a value of -1 or 0 or 1; if m had a value of 2, then ml could have a value of -2 or -1 or 0 or 1 or 2 ... and so on.
* The Bohr atom worked, and it would win him the Nobel Prize for physics in 1922, but even Bohr flatly admitted it left much to be desired. For one thing, it only really worked with the hydrogen atom. Modifying it to work with atoms with more than one electron proved difficult or impossible. It also did not explain at all important features of the hydrogen atom, such as its pattern of chemical bonding. Worst of all, the notion of stationary states was completely arbitrary, no more than a scheme that made things fit, and then only to a degree. Why did the electron only occupy those specific states? The Bohr atomic model was basically a "lash-up", a preliminary theory thrown together with what was at hand.
As with Planck's analysis of blackbody radiation and Einstein's analysis of the photoelectric effect, the Bohr atom gave an answer to a puzzle, but the answer itself simply led to new puzzles. There is a saying that once a can of worms has been opened, the only way to get them back in is to find a bigger can. The physicists would have to keep on finding bigger cans. Bohr was energetic in encouraging others to help solve the puzzles he was investigating, and in 1918 he set up a research organization in Copenhagen that would become known as the Niels Bohr Institute. It attracted many young, energetic minds in physics and was a central location at which ideas were collected and then sent out into the world.
BACK_TO_TOP* In 1923, a French nobleman working on his doctorate named Duke Louis Victor de Broglie (1892:1987) -- the name is pronounced "debroy" and rhymes, implying no irony, with "destroy" -- came up with an idea that provided another piece for the puzzles. Taking a hint from Einstein's analysis of the momentum of a photon:
momentum = Planck's_constant * frequency / speed_of_light
= Planck's_constant / wavelength
-- de Broglie suggested that this was not just a feature of photons, but a feature of all particles. In other words, every particle in the Universe had a wavelength given by:
wavelength = Planck's_constant / momentum
Since Planck's constant is such a small value, the wavelength of an object of any appreciable size moving at any perceptible velocity is too small to be measured, and so for all practical purposes only small particles could demonstrate wave characteristics.
De Broglie came up with his postulate of "wave-particle duality" in a brilliant leap of intuition. His academic supervisor, Paul Langevin (1872:1946), was unsure of what to make of the idea -- after all, de Broglie said that particles acted like waves, but left hanging the question of: "A wave of what?" In classical terms, a wave was an oscillation of a transmission medium, but where was the transmission medium for these "particle waves"?
Langevin sent a copy of de Broglie's dissertation to Einstein. Einstein was impressed, replying: "I believe that it involves more than a mere analogy". In other words, Einstein thought de Broglie was on to something; the precise nature of the wave could be considered later. It would turn out to be quite a puzzle.
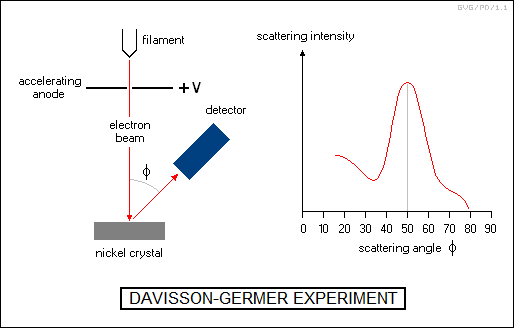
Although once more it was the kind of postulate that posed more questions than it answered, it could be tested by determining if electrons demonstrated wavelike properties, such as diffraction or interference. In 1926, Clinton Davisson (1881:1958) and Lester Germer (1896:1971) of Bell Telephone Laboratories ("Bell Labs") in the US conducted experiments in reflecting electron beams off the surface of nickel crystals. As the angle of the electron beam changed, the reflected electron beam faded in and out due to interference effects. The two researchers hadn't actually been looking for electron diffraction, but they realized that was what was happening, and the Davisson-Germer experiment helped validate de Broglie's proposal.
The classic two-slit interference experiment would have been an even more dramatic demonstration that the electron had wavelike properties, but the wavelength of the electron is so short that setting up such an experiment is extremely demanding. The two-slit electron interference experiment was finally performed by Claus Joennsen in 1961, though by that time few had any serious doubts about wave-particle duality. Interference effects were later observed with heavier particles, and then, beginning in the 1980s, with atoms. They have even been observed with "buckyballs", also known as "soccerene", a molecule with 60 or 70 carbon atoms arranged in a spherical structure reminiscent of a soccer ball, or the "geodetic" dome structures of unorthodox architect R. Buckminster "Bucky" Fuller.
* The idea that electrons -- and other particles -- had wavelike properties was of course puzzling. As with the photon, what sort of wave could be transmitted without a medium to carry it? De Broglie's wave-particle duality postulate hadn't really made the basic question any more baffling than it had been with Einstein's photon postulate, but it certainly greatly widened its scope -- and did nothing to make it any less baffling, either.
It did, however, provide a stepping stone to further revelations. One was that although the wavelike properties of the electron could be observed in at the quantum scale, in the macroscale world of objects that humans could see and deal with, those quantum effects were unnoticeable, and the rules of classical physics applied. This would become a fundamental rule of quantum physics, known as the "correspondence principle", that bridged between the quantum world and the world of classical physics. Bohr had already suggested the idea in his quantum analysis of the hydrogen atom, but wave-particle duality made it more vivid. The correspondence principle is an obvious notion: we only really see quantum effects in the microscale, but those effects sum up to the world of classical physics we see in the macroscale. There's no other way it could be.
Another was that the fact that electrons had a wavelength suggested why electrons in atoms only occupied specific states. Atomic line emission suggested that atoms were some sort of resonant chamber, and if electrons had a wavelength they could be seen to be resonating in such a chamber. Working through such an idea in detail would take a little more time and effort.
* In another half-step forward, in the summer of 1924 an Indian physicist named Satyenda Nath Bose (1894:1974) at the University of Dacca came up with a new approach to the explanation of the blackbody spectrum. He treated light as a "gas" of massless particles and devised a quantum-based statistical analysis that yielded the blackbody curve. It was a very significant half-step: his analysis of black-body radiation made absolutely no mention of electromagnetic waves as such.
Bose's statistical analysis assumed that the particles, the photons, were "indistinguishable". This seems like an arcane concept, but it's a simple idea. If one of three balls is selected from a bin at random, then if all the balls are white and indistinguishable, the result is always a white ball. If the balls are colored red, white, and blue and were distinguishable, then there are three possibilities instead of one. Obviously, results of the statistical analysis of a more complicated system of particles will be very different, depending on whether the particles can be distinguished or not.
Bose sent a paper on his ideas to the physics press. The paper was ignored, so he sent a copy of it to Albert Einstein. Einstein was intrigued, and found that the same analysis also applied to the massive particles in a real gas. The analysis was named "Bose-Einstein statistics". Its significance was not entirely apparent at the time, mostly because under anything resembling normal circumstances it gave the same results as the classical statistical mechanics devised by Maxwell and Boltzmann in the previous century, only coming into effect in very extreme conditions.
For example, helium gas turns into a liquid at 4.18 degrees Kelvin and acts very much like any other liquid, until its temperature is reduced another two degrees, when the predictions of the Bose-Einstein analysis begin to come into play. Below 2.18 degrees Kelvin, which incidentally is not at all easy to reach, about ten percent of the liquid helium becomes a "Bose-Einstein condensate", essentially a single unified macroscale quantum system. The helium's heat capacity and thermal conductivity increase abruptly, its viscosity drops off equally abruptly, and the "superfluid" will do bizarre things, like crawl up the sides of containers and flow over the edge.
BACK_TO_TOP* By the mid-1920s, the ferment of ideas in the emerging study of quantum mechanics was beginning to become frustrating. One physicist described the state of the field at the time as a "lamentable hodgepodge of hypotheses, principles, theorems, and computational recipes." Somebody needed to impose order on the chaos.
One of Bohr's disciples at his Copenhagen institute was a young German physicist named Werner Heisenberg (1901:1976). After a year's study there, Heisenberg obtained a position as an assistant professor to Max Born (1882:1970), director of the physics institute of Goettingen University in Germany. Heisenberg's main preoccupation at the time was the line spectra of atoms. In the spring of 1925 he took a vacation from Goettingen to escape hay fever, and got to thinking about the Bohr atom.
Heisenberg was unsettled by the notion of Bohr's stationary orbits. What kind of an orbit was it that could only have certain radii, with the electrons jumping from one orbit to the next in a "quantum leap" without existing in the space between them? He thought the idea was nonsensical and wondered why anyone would bother to use the word "orbit" in such a context. Heisenberg felt it would simply be better to come up with a way of organizing and manipulating the states of the electron in the hydrogen atom that didn't bother with orbits. He started out simply by tabulating the electron states of the hydrogen atom and the frequencies of photons that would be emitted by transitions between them, as follows:
S1 S2 S3 ...
__________________
S1 f1:1 f2:1 f3:1 ...
S2 f1:2 f2:2 f3:2 ...
S3 f1:3 f2:3 f3:3 ...
... ... ... ... ...
He went from this table of frequencies to develop corresponding tables of amplitudes, positions, and momenta, and began to painfully work out ways of performing calculations with them. He published a paper on it in July 1925, and also of course showed his work to his boss Born before leaving for Copenhagen to rejoin Bohr and his group. Born quickly saw the merit of Heisenberg's ideas and worked with one of his students, Pascual Jordan (1902:1980), to establish them on a more formal basis.
Born realized that Heisenberg's sets of numbers could be represented as a square or rectangular grid of numbers known as a "matrix". Matrix math was already an established branch of mathematics, though it was not well known at the time, and in fact Born was one of the few physicists who understood it. Sets of matrix operations, including addition, subtraction, and multiplication, had been defined; Born and Jordan found that the rules of matrix mathematics could be directly applied to Heisenberg's ideas. Heisenberg was not familiar with matrix math, but it isn't particularly complicated to learn how to use, and Heisenberg picked it up.
Matrix addition is a simple operation, involving addition of the elements of the two matrices to create a third matrix:
| A11 A12 | | B11 B12 | | A11 + B11 A12 + B12 | | | + | | = | | | A21 A22 | | B21 B22 | | A21 + B21 A22 + B22 |
For example:
| 3 7 | | 4 9 | | 3 + 4 7 + 9 | | 7 16 | | | + | | = | | = | | | 2 -5 | | 8 6 | | 2 + 8 -5 + 6 | | 10 1 |
Subtraction is the same, with each element of the second matrix subtracted from each element of the first. Multiplication, however, is a bit more complicated, with the rows of one array multiplied against the columns of the other:
| A11 A12 | | B11 B12 |
| | * | | =
| A21 A22 | | B21 B22 |
| A11 * B11 + A12 * B12 A11 * B12 + A12 * B22 |
| |
| A21 * B11 + A22 * B12 A21 * B12 + A22 * B22 |
For example:
| 3 7 | | 4 9 | | 3 * 4 + 7 * 8 3 * 9 + 7 * 6 |
| | * | | = | |
| 2 -5 | | 8 6 | | 2 * 4 - 5 * 8 2 * 9 - 5 * 6 |
| 12 + 56 27 + 42 |
= | |
| 8 - 40 18 - 30 |
| 68 69 |
= | |
| -32 -12 |
If the order of the multiplication is changed, something interesting happens:
| 4 9 | | 3 7 | | 4 * 3 + 9 * 2 4 * 7 - 9 * 5 |
| | * | | = | |
| 8 6 | | 2 -5 | | 8 * 3 + 6 * 2 8 * 7 - 6 * 5 |
| 12 + 18 28 - 45 |
= | |
| 24 + 18 56 - 30 |
| 30 -17 |
= | |
| 40 26 |
The results are completely different: matrix multiplication is "non-commutative", or more formally "non-Abelian". Unlike ordinary multiplication of single ("scalar") numbers, the order of matrix multiplication is important: A * B does not equal B * A. The relevance of this non-commutative multiplication was that if Heisenberg multiplied the matrices for momentum (p) and position (q) in different orders and subtracted them, the difference was always the same:
p * q - q * p = (Planck's_constant / 2PI) / i
-- where "i" is the "imaginary number", the square root of -1. The "i" factor isn't particularly important here; the main thing to notice is that the difference was always Planck's constant divided by 2PI. At the time, Heisenberg had no idea what this meant and found it very frustrating. However, he talked it out with his colleagues and, in 1926, Heisenberg, Born, and Jordan published a detailed paper on the concept. The fully developed theory acquired a name: "matrix mechanics". A young Austrian physicist named Wolfgang Pauli (1900:1958), noted both for his brilliance and his willingness to light into other physicists whose views he considered incorrect, decided to use matrix mechanics to determine the line spectra of the hydrogen atom. Pauli's work gave exactly the same results as the Bohr model -- and also explained Zeeman splitting.
Not everybody was happy with matrix mechanics. As noted, few physicists of the era were comfortable with manipulating matrices, and in general the reaction was that coming to grips with Heisenberg's matrix mechanics was a pain. Indeed, Heisenberg, Pauli, and others working on it were finding it difficult to come up with the right answers, though they had faith they would get there in the end.
Worse, Heisenberg had abandoned any pretense of putting together a theory based on visualizing the structure of an atom: he simply had a set of rules that gave the right results. That was sensible, because the structure of an atom isn't visualizable, it's not like anyone can see into it in a visual sense with any equipment. All physics of the structure of the atom was derived from observations made with instruments, and not by direct visual observation; all the model did was provide a framework that made sense of the observations -- it was a set of accounting rules, in effect, that gave the observed results. How else could it work? Nonetheless, some physicists were unhappy with that idea. They weren't going to get any happier.
BACK_TO_TOP* While Heisenberg, Born, and Jordan were tinkering with matrix mechanics, an Austrian physicist named Erwin Schroedinger (1887:1961) was taking another approach to the analysis of the atom. Schroedinger, who up to that time had not made any significant contributions to physics, had been working on de Broglie's proposal that particles had a wavelength since 1924 and ended up going in circles. At the end of 1925, he took a vacation in the Alps with one of his mistresses -- he had a freewheeling romantic life and didn't let little things like his wife get in the way, nor did she have a problem with it -- and his thinking finally congealed, leading to the publication of a paper in March 1926.
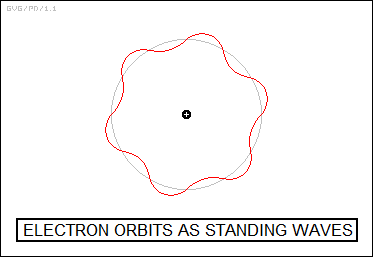
Schroedinger took the concept of the hydrogen atom as a resonant chamber for electrons and postulated that the stationary states of the electron in the hydrogen atom that had been described in the Bohr atomic model amounted to electron standing waves, orbits that had a circumference an exact multiple of the half-wavelength of the electron.
He then created his famous "Schroedinger equation", which could be used to define the "wavefunction", of the electron in the hydrogen atom, with the wavefunction assigned the trident-like upper-case Greek letter PSI as a symbol:
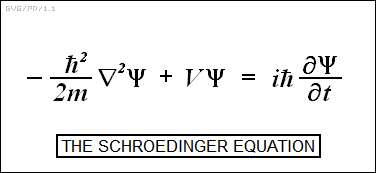
A detailed discussion of the Schroedinger equation is beyond the scope of an introductory text. It is not extremely complicated in itself, being nothing more than a differential equation that would not particularly intimidate any second-year physics or engineering student, but its precise form unsurprisingly depends on the system being described. It is not too hard to solve for the one-electron hydrogen atom; can be solved with substantially more difficulty for the two-electron helium atom; but becomes increasingly difficult to solve as atoms grow any more complicated. In fact, there is no exact solution of the Schroedinger equation for atoms larger than helium, though approximate solutions can be found to any desired practical level of accuracy.
It is possible, however, to bypass the math and come up with a simple "solution" to the Schroedinger equation for a very artificial system: the "infinite square well". This is somewhat misleading name; the alternate common name, the "electron in a box", is only somewhat better. What this scenario imagines is that an electron is trapped in a tiny tube that has a fixed length and effectively zero diameter. The electron cannot escape from this tube, no matter how much energy it obtains from photons fired into the tube. The tube acts as a resonant chamber for the electron: the only electron "wavefunctions" that can exist in it are standing waves, with an integer number of half wavecycles. De Broglie had shown that the wavelength and momentum for any particle are given by the relationship:
momentum = Planck's_constant / wavelength
The wavelengths of the electron trapped in the tube are constrained to:
wavelength = 2 * tube_length / N
-- where "N" is an integer from 1 to infinity. The "2" comes in, remember, because the tube accommodates an integer multiple of half wavecycles. The values of wavelength for values of N are as follows:
N wavelength (in tube_lengths)
____________________________________
1 2 (half a wavecycle)
2 1 (one full wavecycle)
3 2/3 (three half wavecycles)
4 1/2 (two full wavecycles)
5 2/5 (five half wavecycles)
...
____________________________________
Combining the formula for the de Broglie wavelength and the allowed wavelengths in the tube gives:
momentum = Planck's_constant / ( 2 * tube_length / N )
= N * Planck's_constant / ( 2 * tube_length )
It's a simple fact from classical physics that kinetic energy and momentum are related as follows:
energy = ( momentum^2 ) / ( 2 * mass )
This means that the allowed energy values of the electron in the tube are:
( N * Planck's_constant / ( 2 * tube_length ) )^2
energy = ----------------------------------------------------
2 * electron_mass
( N^2 ) * Planck's_constant^2
= -------------------------------------------
2 * electron_mass * ( 2 * tube_length )^2
( N^2 ) * Planck's_constant^2
= -----------------------------------
8 * electron_mass * tube_length^2
A free electron that is not confined can have a continuous range of energies, but once it is stuck in this tube or other confined space, its energy is quantized. The lowest energy state of an electron in the tube corresponds to N = 1. This is the "ground state" of the electron in the tube; the electron cannot have any lower value of energy. If the electron were energized, say by absorbing a photon, it will be promoted to a higher energy state with a higher value of N. The electron might then fall to a lower energy state, emitting a photon with an energy corresponding to the difference between the two energy states.
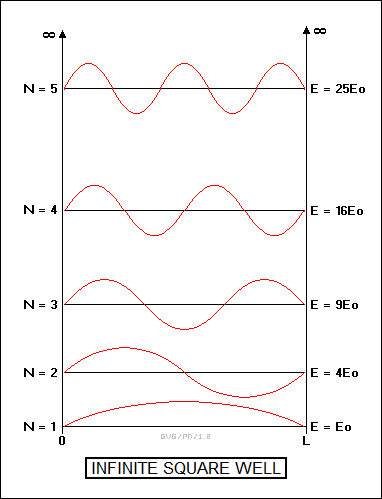
It is fairly simple to construct a "line spectrum" for the tube -- the infinite square well -- though since the infinite square well doesn't really exist, this is mostly an academic exercise. However, the same sort of approach does apply to real world systems such as the hydrogen atom, though cooking up the solution is trickier.
In any case, Schroedinger felt he had come up with an answer that upstaged matrix mechanics, and in many ways it had. Physicists were much more familiar with waves and their mathematical manipulation, so they were inclined to be much more comfortable with the Schroedinger equation than matrix mechanics. Furthermore, Schroedinger felt that by simply accepting that electrons were both particle and wave, he had banished Heisenberg's uncomfortable notion that the workings of the hydrogen atom could not be directly visualized.
Schroedinger was right to an extent; the Schroedinger equation would generally overshadow matrix mechanics. However, it didn't kill matrix mechanics off. In late 1925, Heisenberg had gone to Britain, where he presented a lecture on his ideas. One of the members of the audience was a silent, single-minded, withdrawn, and extremely brilliant English mathematical physicist named Paul Adrien Maurice ("PAM") Dirac (1902:1984), who picked up the concepts and ran with them, fleshing them out as a formal theory.
In 1926, Dirac published a paper, titled "The Fundamental Equations Of Quantum Mechanics". It was an outstanding document that did much to nail down the formal mathematics of quantum mechanics; it also showed that matrix mechanics and the Schroedinger equation were simply different ways of expressing exactly the same thing. Schroedinger himself ended up demonstrating the equivalence as well. Matrix mechanics might have been sidelined, but it was not disproven in any way, very much the opposite. Much more importantly, Schroedinger had by no means shut off the flood of complications that were being created by the new physics.
BACK_TO_TOP* Schroedinger basically took the question of how a particle can also be a wave at face value: an electron acted like a particle, propagating across free space, but it had wavelike characteristics, such as interference effects. Matter simply had the form of a wave at such scales. If that was the way the Universe worked, so be it: obviously things worked differently at the sub-microscopic "quantum" level than they did in the macroscale world that humans perceive and deal with directly. This was and remains a fairly useful simple model for those who don't want to, or need to, get into any further details -- the concept is often summarized as "shut up and calculate".
However, consideration of further details showed that the "matter wave" concept was also clearly not correct. If an electron was actually smeared out over a wave, then its properties, such as its electric charge, were smeared out as well. All actual observations of electrons revealed point objects of absolutely minimal dimensions.
Max Born had originally been attracted by the elegance of the Schroedinger equation, feeling that it was much superior to the computationally painful matrix mechanics that he and his colleagues had been working on, but Born gradually came to the conclusion that Schroedinger was not so much answering the question of wave-particle duality, so much as he was dodging it. There wasn't an answer to it, it was just the way things were observed to be, and no model, no set of accounting rules, could change the fact that the quantum realm operated in a way contrary to the world of classical physics.
Born decided that the Schroedinger wavefunction actually gave the probability of detecting the electron at a particular location -- or more correctly, he said that the square of the absolute value of that wavefunction:
SQR ( ABS ( PSI ) )
-- gave the probability of finding the electron at a particular location. Notice the use of the word detecting in this context; there's an important subtle distinction in this usage that is discussed later. Born's postulate explained electron interference, since where two electron wavefunctions canceled each other out the probability of finding the electron was low or zero, and where they added up the probability was high, resulting in the interference pattern.
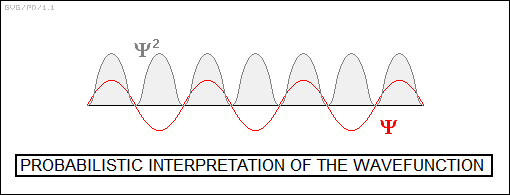
Born's vision of the quantum world didn't make everyone happy, either; in fact, the probabilistic interpretation of the Schroedinger wavefunction had features that many physicists found somewhere between "distressing" and "infuriating", seemingly embracing impossibilities.
We have already examined the wavefunction for the "electron in a box" or "infinite square well" scenario, in which an electron is completely trapped inside a tube. Now suppose the tube was constructed so that if the electron had a high enough energy, it could punch through the ends of the tube, which are visualized here as thin walls; this modified scenario can be referred to as the "non-infinite square well". With the infinite square well, the Schroedinger equation resulted in a wavefunction that was zero at the ends of the tube. In the non-infinite square well, since the electron has a chance of escaping from the tube, the wavefunction is not zero, and in fact falls off to zero in a smooth curve through the ends of the tube. What this means is that the electron has some finite probability of "leaking" or "tunneling" out of the ends of the tube, even if it doesn't seem to have enough energy to do so. This phenomenon is known as "quantum mechanical tunneling"; it is often observed in electronic devices and atomic processes.
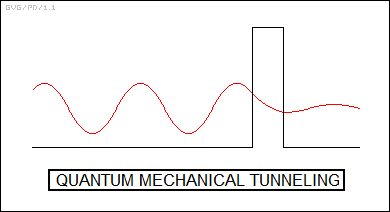
Quantum-mechanical tunneling can be proven by experiment and experience, so even though it's annoying from the point of view of classical physics, it is hard to refute. However, there was a more fundamental reason to object to Born's ideas. Probabilities are, after all, just that, probabilities. Suppose that Alice, a physics student, tosses a fair die a large number of times, it will come up as any one of its six values -- "six" or "one" or whatever -- about one-sixth of the time, approaching exactly one-sixth as the number of tosses increases. Probability does not allow anyone to predict what the result of an actual single fair toss of the die will be. The odds can be calculated, but the result of the toss is otherwise completely random and unpredictable.
What Born was saying was that there was no way to predict the behavior of any single electron, though the behavior of large numbers of electrons was highly predictable, becoming ever more predictable as the numbers increased. Schroedinger rejected the idea, Planck sided with him, and Einstein, in a tactful letter to Born, said that he felt that quantum mechanics was "imposing" but added that "an inner voice tells me that it is not yet the real thing." Einstein gradually boiled this thought down to a simple well-known slogan: "God does not play dice with the Universe."
Born defended his ideas, replying to Einstein: "If God has made the world a perfect mechanism, He has at least conceded so much to our imperfect intellect that in order to predict little parts of it, we need not solve innumerable differential equations, but we can use dice with fair success."
In effect: so what if we couldn't have absolute determinism? It was absurd to think it was possible even before quantum physics, there being no way to observe the Universe down to such a level of detail as to rule out any unknown factor. We can still calculate the odds and win at the game. Bohr, who would side with Born, had a tidier and also well-known reply to Einstein: "Stop telling God what to do."
The battle over quantum foundations was not in general bloodthirsty. Schroedinger, an easy-going man, basically ended up staying quiet on the matter. Heisenberg won the Nobel Prize for his work in 1932; he couldn't collect on it until 1933, the year Schroedinger and Dirac shared the prize. Heisenberg and Schroedinger accepted their prizes together on stage in a show of mutual graciousness. Still, Schroedinger was not happy with the way his wave equation had been hijacked by the opposition, saying: "I don't like it, and I wish I'd never had anything to do with it."
Incidentally, Heisenberg's Nobel Prize caused him some embarrassment, since he was aware that his efforts owed much to Born and Jordan. Heisenberg sent a letter to Born to acknowledge the debt, but Born remained annoyed at the Nobel Committee for years. Born finally won the Nobel in 1954, and as far as he was concerned it was about time. That was Heisenberg's feeling as well, expressing his relief over the award to Born. Pascual Jordan did not share in the award; some suspect he was overlooked because he had been an enthusiastic Nazi.
BACK_TO_TOP* Wolfgang Pauli was less an innovator than a critic, a good one, able to give the ideas of others a thorough "wire-brushing" to see if they would stand up under scrutiny. He was valued for this ability, though it was not always pleasant being on the receiving end, since he rarely suffered foolish or even questionable ideas patiently. As a graduate student, he had notoriously commented after a lecture by Albert Einstein: "What Professor Einstein said is not so stupid." When particularly disgusted, Pauli would deliver a condemnation that physicists like to use to this day: "Das ist nicht nur nicht richtig -- es ist nicht einmal falsch!" In English: "That is not just not right -- it isn't even wrong!"
Pauli did accept the probabilistic nature of the Schroedinger wavefunction and began to consider its implications. In 1925, he published an analysis of the wavefunctions of particles that demonstrated they had an interesting property.
During the development of quantum physics up to this time, physicists had defined a concept known as "spin" for elementary particles. The Bohr atomic model had evolved from a single primary quantum number n to add the orbital quantum number m and then the magnetic quantum number ml. That still did not account for the fine splitting of spectral lines of certain elements in a magnetic field. There was also the fact that, in 1922, two German researchers, Otto Stern (1889:1969) and Walter Gerlach (1889:1979), had "fired" silver atoms from an oven down an extended magnetic field with a strong vertical gradient into a photographic plate. The silver atoms split up into two different and distinct streams as they passed through the magnetic field. Obviously, the silver atom had some sort of quantized magnetic "state" that had only two values.
In late 1924, Pauli had suggested that the fine splitting was caused by a quantum state of the electron that could have two and only two values, though he was not exactly sure what they were values of. In the summer of 1925, two Dutch physicists, Samuel Goudsmit (1902:1978) and George Uhlenbeck (1900:1988), who came up with the idea that this quantum state corresponded to the spin of the electron. It could spin in an up direction or a down direction.
There were technical problems with the idea. An American physicist named Ralph de Laer Kronig (1904:1995) had suggested the same idea to Pauli, and Pauli immediately lit into it so vehemently that Kronig didn't bother to publish it. Goudsmit and Uhlenbeck found out after they submitted their paper for publication that their theory implied that the electron rotated at ten times the speed of light, which was an impossibility, but the critique was based on the reasoning of classical physics. Bohr and Einstein commented on seeing their paper that once quantum theory was better developed, the problem would go away, and it did.
Spin is related to the magnetic properties of an electron. Moving charges, as Maxwell had shown, produce a magnetic field, and so the spin of the electron produces a magnetic field. This spin-induced electron magnetic field is manifested by the "magnetic moment" of the electron. Magnetic moment is the amount of energy required to turn a magnet sitting in a magnetic field of given strength from being aligned to the field to being perpendicular to the field. Since magnetic field strength is given in "teslas", then magnetic moment is given in "joules per tesla", and the symbol for it is given by the lowercase version of the Greek character "mu". The magnetic moment of the electron is 9.27E-14 joules per tesla, a value which is used as a reference and is known as the "Bohr magneton", abbreviated as "mu-sub-B", meaning "mu" with a subscript "B".
* Spin became accepted and other particles were found to have spin, but to complicate matters, there are two different classes of particles: those that can only have spin values of 0, 1, 2, 3, ... and so on; and those that can only have spin values of 1/2, 3/2, 5/2, ... and so on. (These values are technically factors of the constant hbar, but hbar is usually left implied for simplicity.) These two classes of particles have very different characteristics.
The best-known "integer spin" particle is the photon. The statistical behavior of the photon and other integer spin particles was established by Bose and Einstein with their Bose-Einstein statistics, and so integer spin particles became known as "bosons". The best-known "half-integer" spin particle is the electron, which can take spin values of 1/2 and -1/2. In 1926 and 1927, Paul Dirac and the Italian physicist Enrico Fermi (1901:1954) -- then working at the University of Rome in a research laboratory directed by a visionary named Orso Mario Corbino (1876:1937) -- established the statistical behavior of the electron and other half-integer spin particles. Their approach was unsurprisingly named "Fermi-Dirac statistics", and so half-integer spin particles were named "fermions".
It must be emphasized that the term "spin" in this context does not exactly imply a spinning little ball as such. The term was introduced because the scenario could be loosely modeled that way, but the spinning little balls we are familiar with aren't restricted to certain very specific values of spin. Worse, one of the aspects of the theory of electron spin is that spinning an electron around once doesn't actually bring it back to its initial position; it has to be spun around twice. The British astrophysicist Sir Arthur Stanley Eddington (1882:1944) suggested that using the term "spin" in this context was misleading. Leveraging off Lewis Carroll's famous nonsense verse JABBERWOCKY and its line "did gyre and gimbal in the wabe", he suggested that the term "gyre" would be just about as exact and much less misleading.
* The behavior of bosons and fermions was defined by their wavefunctions as established by solutions of the Schroedinger equation, and these solutions had to take spin into account. Doing so led to the revelation that bosons had "even" wavefunctions while fermions had "odd" wavefunctions. This sounds once again like a bizarre notion, but it's easy to see in itself: an even function is one that, when reversed, looks the same. The cosine function is a simple example of an even function. In contrast, an odd function is one that, when reversed, is the negative of itself. The sine function is a simple example of an odd function.
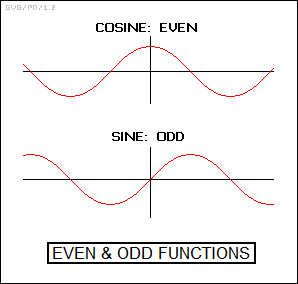
Now consider what happens when we take two identical particles, bring them closer together, and observe their composite Schroedinger wavefunction, which is the sum of the wavefunctions of the two particles. For two identical bosons with integer spin, the even wavefunctions of the two particles add up. This means that the probability of having two bosons in the same state is high, and this simple probability amounts to an effective force that draws bosons together. This force is what causes the bizarre behavior of Bose-Einstein condensates.
In general, bosons tend to be drawn together to operate as a system. It is by no means coincidental that the photon, the quantum element of the electromagnetic field, is a boson, since the collective "herd" behavior of bosons allows assemblies of photons to be seen, at a somewhat higher level, as a classic electromagnetic field. In fact, for this reason, any particle that is the quantum element of a classic field has to be a boson.
However, if two identical fermions with half-integer spin are brought together, their odd waveforms cancel out. That means that the probability of finding them together is zero. Pauli simply stated that two fermions cannot occupy the same state. This rule became known as the "Pauli exclusion principle". He would get the Nobel Prize for this work in 1945.
The exclusion principle was far from being of purely academic interest. Many of the properties of atoms, most specifically the patterns of chemical bonding that were displayed in the neat order of the periodic table of the elements, began to make sense once the exclusion principle was applied. Chemistry then ceased to be an empirical science that simply cataloged atoms and described how they behaved; the exclusion principle turned it into a theoretical science that could give an underlying rationale for their behavior.
BACK_TO_TOP